Le equazioni matematiche: cos'è l'identità
L’identità in matematica è un concetto che rappresenta un’equazione che è vera per tutti i valori delle variabili in essa contenute. È una relazione che esprime un fatto matematico fondamentale, valido in un ampio contesto o addirittura universalmente. Un esempio classico è l’identità £$b ^2 =(a+b)(a−b)$£, che è vera per tutti i valori reali di a e b.
Il collegamento tra identità e equazioni è sottile ma importante. Mentre un’identità è sempre vera per tutte le possibili sostituzioni dei valori delle sue variabili, un’equazione può essere vera solo per alcuni valori specifici delle sue variabili. Ad esempio, l’equazione £$x+2=5$£ è vera solo quando x è 3. Le equazioni, dunque, sono come domande che chiedono “per quali valori di questa affermazione è vera?”, mentre le identità affermano “questa relazione è sempre vera, indipendentemente dai valori delle variabili”.
Le identità sono strumenti potenti nella risoluzione delle equazioni. Conoscere e riconoscere identità comuni può semplificare significativamente il processo di risoluzione, permettendo di ristrutturare o semplificare un’equazione in una forma più gestibile. Ad esempio, nel risolvere equazioni quadratiche, l’identità di scomposizione dei quadrati perfetti può essere usata per trasformare rapidamente l’equazione in una più semplice da risolvere.
In matematica, le identità vengono utilizzate anche per costruire definizioni, teoremi e prove. Sono fondamentali nella costruzione logica di molte aree della matematica, dalla geometria all’algebra, dal calcolo all’analisi matematica. La loro universalità le rende uno strumento essenziale per comprendere e manipolare concetti matematici a vari livelli.
Scopriamo insieme cos’è più nel dettaglio e qual è il legame tra identità ed equazioni.
- Che cos'è un'identità in matematica
- Che cos'è un'equazione e qual è la sua identità
- Equazioni di primo grado e identità
Che cos’è un’identità in matematica
Prima di parlare di equazioni, capiamo bene cos’è un’identità.
Un’identità è un’uguaglianza sempre vera. Cioè abbiamo due espressioni letterali, due numeri, due frazioni, … uguali da una parte e dall’altra dell’uguale!
£$ 3 = 3 $£ è un’identità, ma anche £$ 32a = 32a $£ è un’identità perché è un’uguaglianza vera, qualunque sia il valore di £$ a $£.
Possiamo dire che un’identità è una bilancia sempre in equilibrio. Abbiamo già incontrato le identità studiando matematica: ogni volta che risolviamo un’espressione e troviamo il risultato corretto, siamo di fronte ad un’identità.
L’espressione iniziale è uguale al risultato che troviamo alla fine: anche se a prima vista sembrano due cose completamente diverse, hanno lo stesso valore.
Che cos’è un’equazione e qual è la sua identità
Risolvere un’equazione… Con la bilancia!
La prima equazione mai scritta

Un’identità è un’uguaglianza sempre verificata, quindi una bilancia sempre in equilibrio.
Un’equazione è, più semplicemente, un’uguaglianza tra due espressioni dove compare almeno un’incognita che indichiamo con una lettera dell’alfabeto. Il termine equazione, infatti, significa proprio uguaglianza.
Con le equazioni e il calcolo letterale, possiamo iniziare a parlare di algebra. Con l’algebra introduciamo il concetto di “sconosciuto”. A differenza delle identità, l’uguaglianza in un’equazione non è sempre vera. Con le equazioni leghiamo qualcosa che non conosciamo a qualcosa che conosciamo, in modo da riuscire a trovare il valore dell’incognita.
Esempio: £$ 3x + 5 = 17 $£ è un’equazione: un’uguaglianza tra due espressioni che contiene un’incognita, la £$ x $£.
Per risolvere un’equazione, dobbiamo trovare il valore per l’incognita che rende vera l’uguaglianza, cioè che porta la bilancia ad essere in equilibrio.
Possiamo trovare un’equazione a partire da una qualsiasi espressione: prima di risolverla, non conosciamo il risultato, quindi questa è la nostra incognita!
L’obiettivo è quello di risolvere l’equazione, cioè trovare il valore dell’incognita e quindi, in questo caso, il risultato dell’espressione.
Esempio: £$ 4+ 5 – 6 $£ è una semplice espressione. Possiamo “farla diventare” un’equazione semplicemente aggiungendo l’uguale e l’incognita: £$ 4 + 5 – 6 = x $£.
Risolvere questa equazione, cioè trovare il valore della £$ x $£, equivale a risolvere la nostra espressione.
Il risultato è semplicemente £$ 3 = x $£ che possiamo leggere da sinistra verso destra o da destra verso sinistra, £$ x = 3 $£.
Equazioni di primo grado e identità
Come risolvere un’equazione?
Quanto vale l’incongnita?
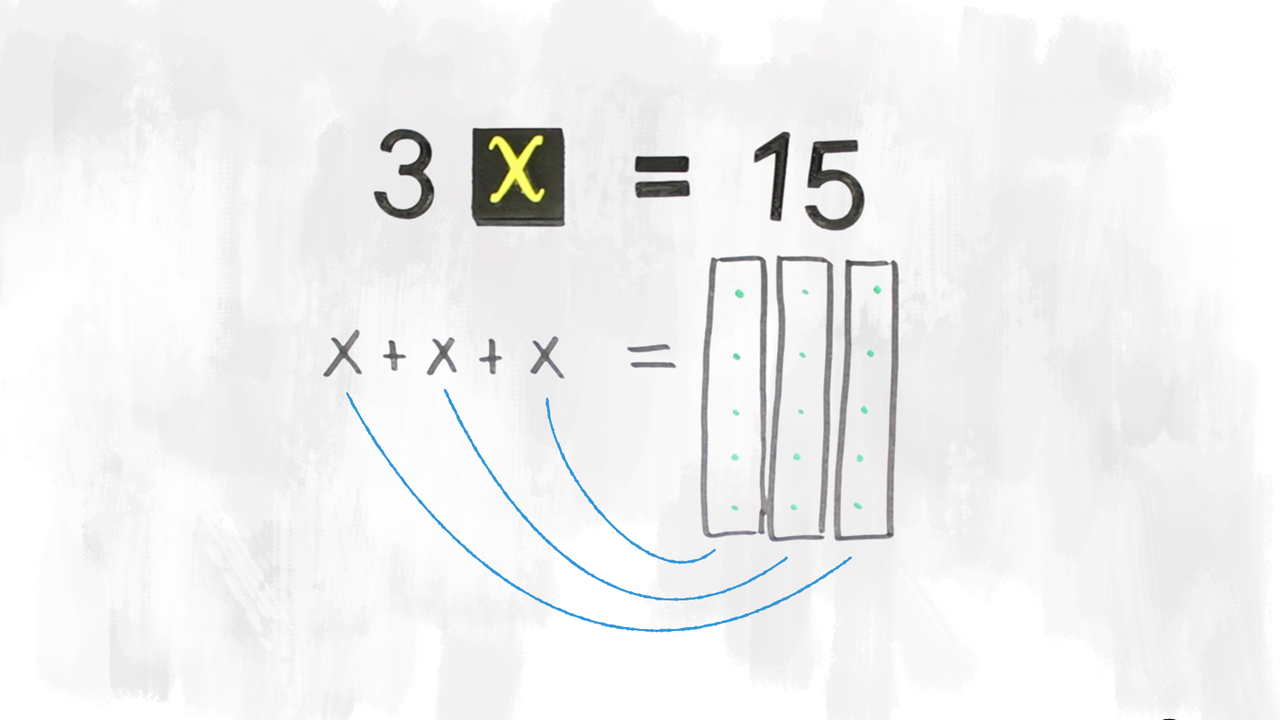
Abbiamo studiato i monomi e i polinomi e abbiamo scoperto come riconoscere di quale grado sono.
Le equazioni sono uguaglianze tra espressioni che contengono almeno un’incognita, quindi sono ancora delle espressioni letterali, in particolare possono essere uguaglianze tra polinomi.
Possiamo capire il grado dell’equazione trovando il grado delle espressioni letterali.
Determinare il grado di un’equazione, quindi, è semplice: basta determinare il grado delle espressioni letterali che la compongono e scegliere il grado massimo.
Noi andremo ad analizzare in modo più approfondito le equazioni lineari, o equazioni di primo grado, cioè quelle equazioni in cui l’incognita compare con esponente uguale a £$ 1 $£.

La soluzione (o radice) è £$ x = \frac{b}{a} $£.
Esempio: £$ 5 x = 15 $£ è un’equazione di primo grado in forma normale. La sua soluzione è £$ x = 3 $£.
Sono equazioni di primo grado anche queste:
- £$ 5x + 3a – 2k = 47 $£
- £$ 52b – 6 = 8 $£
- £$ \frac{6}{11} x + 4 = 2 $£
