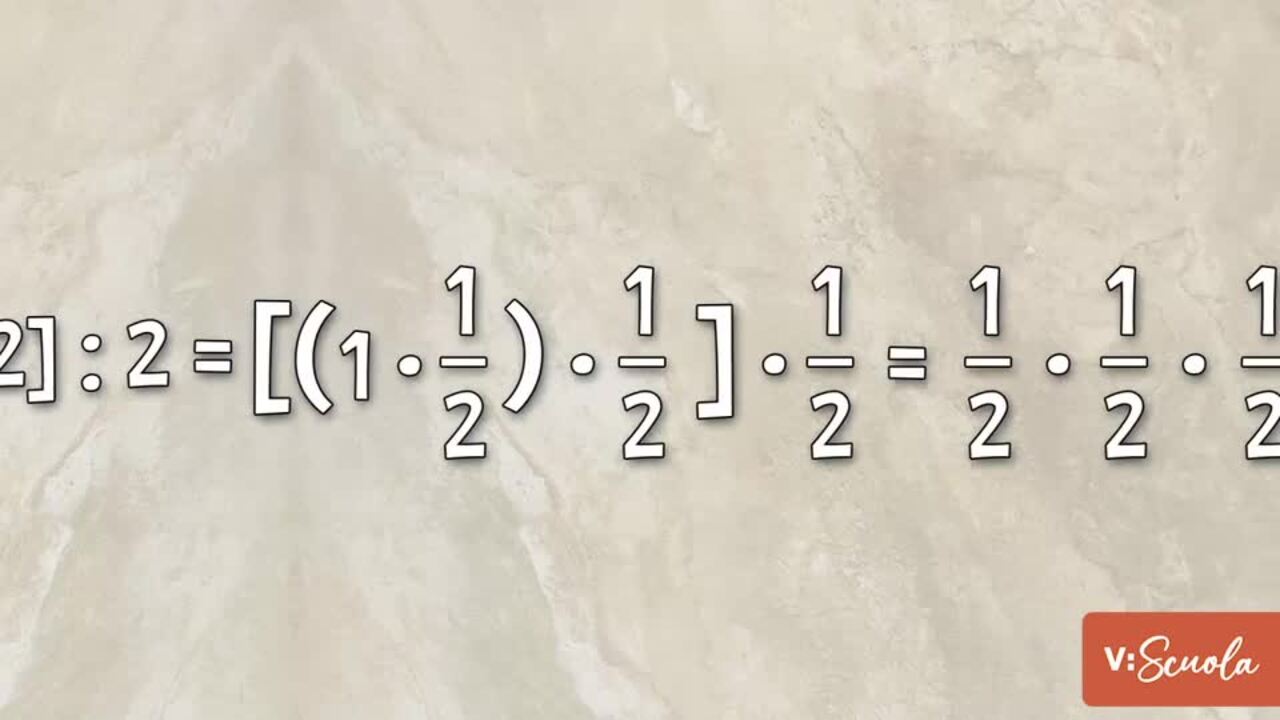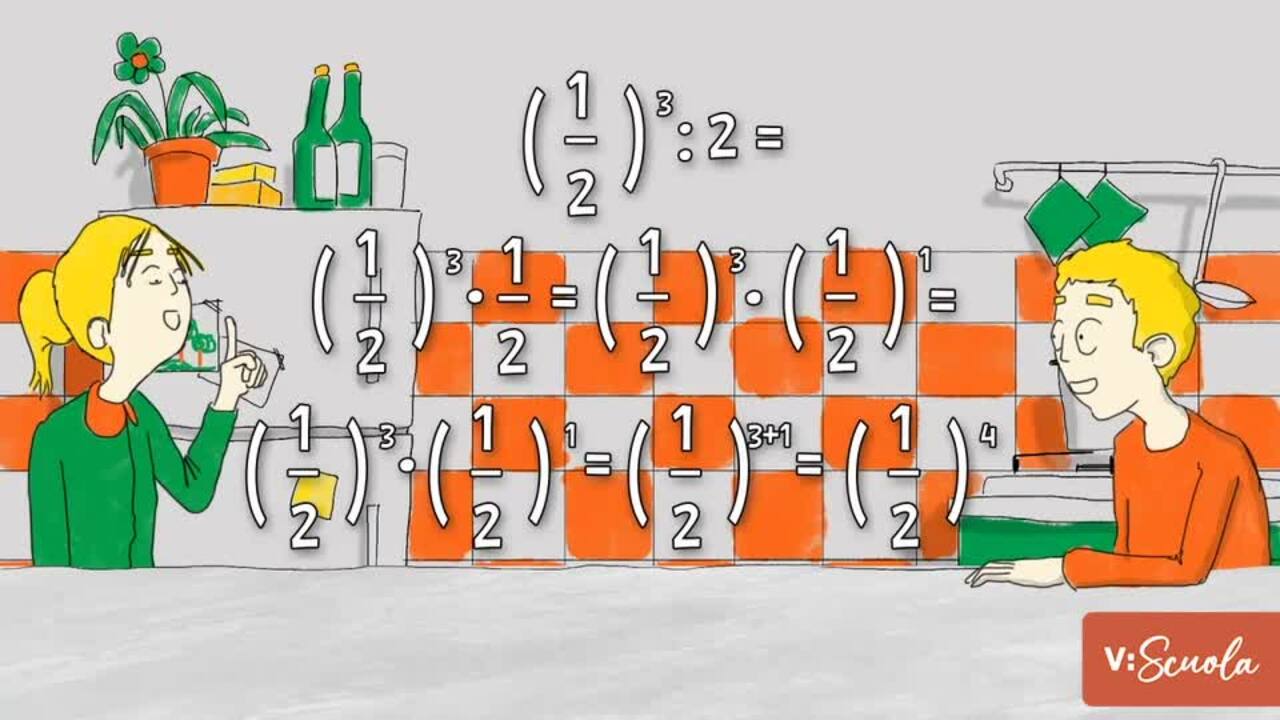Prerequisiti per ripassare le potenze di frazioni
Prerequisiti per ripassare le potenze di frazioni sono:
Caricamento in corso...
Potenze di frazioni
Potenze di frazioni: come si calcolano? L'elevamento a potenza di una frazione è una potenza che ha per base una frazione e per esponente un numero naturale e segue le stesse regole e proprietà delle potenze dei numeri naturali. Impara a risolvere le espressioni con frazioni e potenze e non dimenticarti le parentesi: altrimenti starai elevando a potenza soltanto il numeratore della frazione!
Appunti
Le espressioni con frazioni e potenze ti preoccupano? Impara a risolvere le potenze di frazioni e tieniti pronto per la verifica di matematica!
Hai imparato come fare addizioni e sottrazioni tra frazioni: basta trovare il denominatore comune tra le due frazioni per poi sommare o sottrarre i numeratori. Sai già che per svolgere il prodotto tra frazioni bisogna "semplificare in croce e moltiplicare in riga" e che la divisione tra frazioni non è altro che una moltiplicazione per il reciproco!
Ma come fare la potenza di unafrazione? Anche se la base è una frazione si tratta sempre di una moltiplicazione ripetuta: devi perciò moltiplicare la frazione per se stessa tante volte quante ne indica l'esponente. Basta elevare a quella potenza sia il numeratore che il denominatore.
Per le potenze di frazioni sono molto importanti le parentesi! Scrivere £$\left( \frac{3}{5} \right)^2 $£ è diverso che scrivere £$ \frac{3}{5}^2$£ perché in £$ \frac{3}{5}^2 = \frac{3^2}{5}$£ si eleva a potenza soltanto il numeratore!
Esercitati sulle potenze di frazioni con gli esercizi svolti dei tre livelli prima di passare alle espressioni con le frazioni: rispetta l'ordine delle operazioni e le frazioni non avranno più segreti per te!
Contenuti di questa lezione su: Potenze di frazioni
Potenza di una frazione
La potenza di una frazione è il prodotto di tante frazioni uguali quante ne indica l’esponente. Per esempio £$ \left( \frac{5}{4}\right)^2=\frac{5}{4} \cdot \frac{5}{4} $£. Per calcolare il prodotto di frazioni, semplifichiamo in corce e moltiplichiamo in riga, quindi: £$ \frac{5}{4} \cdot \frac{5}{4} = \frac{5 \cdot 5}{4 \cdot 4}= \frac{5^2}{4^2} $£
Per calcolare la potenza di una frazione basta quindi calcolare la potenza del numeratore fratto la potenza del denominatore.
Esempio: £$ \left( \frac{2}{3} \right)^2 = \frac{2^2}{3^2} = \frac{4}{9} $£
Attenzione! È molto importante mettere le parentesi per fare la potenza di una frazione. La parentesi indica che vuoi elevare tutta la frazione e non solo uno fra numeratore e denominatore. Per esempio: £$\left( \frac{7}{5} \right)^2 $£ è diverso da £$ \frac{7}{5}^2$£, infatti £$\left( \frac{7}{5} \right)^2= \frac{49}{25} $£, mentre £$ \frac{7}{5} ^2= \frac{7^2}{5} = \frac{49}{5} $£
Proprietà delle potenze con la stessa base nelle frazioni
Le proprietà delle potenze valgono anche per le potenze di frazioni. Ripassiamo le proprietà delle potenze con la stessa base.
Nelle potenze di frazioni, prodotto di due potenze con la stessa base è uguale ad una potenza che ha per base la stessa frazione, ma come esponente la somma degli esponenti.
Esempio: £$ \left( \frac{2}{3} \right)^5 \cdot \frac{2}{3} = \left( \frac{2}{3} \right)^{5 + 1} = \left(\frac{2}{3} \right)^6 $£
Il quoziente di due potenze di frazioni con la stessa base è una potenza che ha per base la stessa frazione, ma per esponente la differenza tra i due esponenti.
Esempio: £$ \left( \frac{2}{3} \right)^5 : \frac{2}{3} = \left( \frac{2}{3} \right)^{5 - 1} = \left(\frac{2}{3} \right)^4 $£
Attenzione! Ricordati sempre di scrivere le parentesi, altrimenti devi elevare solo il numeratore della frazione!
Proprietà delle potenze con lo stesso esponente nelle frazioni
Per il prodotto ed il quoziente tra frazioni che sono elevate allo stesso esponente valgono ancora le proprietà delle potenze con lo stesso esponente.
Per calcolare la moltiplicazione tra due frazioni con lo stesso esponente, non dimenticare le proprietà delle potenze: il risultato del prodotto è una frazione che ha per base il prodotto tra le due basi e per esponente lo stesso esponente.
Esempio: £$ \left( \frac{3}{5} \right)^2 \cdot \left( \frac{4}{3} \right)^2 = \left(\frac{3}{5} \cdot \frac{4}{3} \right)^2 = \left(\frac{4}{5}\right)^2 $£
Per calcolare la divisione tra due frazioni con lo stesso esponente applichiamo di nuovo la stessa proprietà: il quoziente sarà una potenza che ha per base il quoziente tra le due basi e per esponente lo stesso esponente.
Esempio: £$ \left( \frac{3}{5} \right)^2 : \left( \frac{4}{3} \right)^2 = $£ £$ \left(\frac{3}{5} : \frac{4}{3} \right)^2 =$£ £$ \left(\frac{3}{5} \cdot \frac{3}{4} \right)^2 $£ £$= \left(\frac{9}{20}\right)^2 $£
