Minimo comune multiplo e massimo comune divisore: cosa sono
Il Massimo Comun Divisore ( M.C.D.) e il minimo comune multiplo (m.c.m.) ci permettono di calcolare tutti i divisori o i multipli comuni di due o più numeri. Scopri la definizione di M.C.D. e m.c.m. e le loro proprietà.
Il Massimo Comun Divisore tra due o più numeri è il più grande tra i divisori che quei numeri hanno in comune. Il minimo comune multiplo, invece, è il più piccolo tra i multipli che due o più numeri hanno in comune.
Sappiamo infatti che i numeri hanno multipli e divisori. Ma numeri diversi possono avere gli stessi multipli o gli stessi divisori? Certo! Non serve trovarli tutti, ma ce ne sono alcuni un po’ particolari che vedremo in questo articolo.
Pronti? Cominciamo insieme a capire meglio questi due elementi matematici così importanti!
- Il Massimo Comun Divisore (M.C.D.)
- Il minimo comune multiplo (m.c.m.)
- Proprietà e relazioni tra Massimo Comun Divisore e minimo comune multiplo
Il Massimo Comun Divisore (M.C.D.)
Tra tutti i divisori di un numero è interessante trovare il massimo, cioè il più grande. Il Massimo Comun Divisore (M.C.D.) tra due (o più) numeri è il più grande tra i divisori che hanno in comune.
Per facilitare la ricerca del Massimo Comun Divisore, seguiamo questo procedimento:
- scomponiamo i numeri in fattori primi;
- moltiplichiamo i fattori comuni prendendoli una volta sola, con l’esponente più piccolo.
Esempio: £$ \text{M.C.D.}(36, 48) = 12 $£ infatti se scomponiamo in fattori primi troviamo £$ 36 = 2^2 \cdot 3^2 $£ e £$ 48 = 2^4 \cdot 3 $£. Per trovare il M.C.D., scegliamo i fattori comuni con l’esponente minore, quindi £$ \text{M.C.D.}(36, 48) = 2^2 \cdot 3 = 12 $£.
Può capitare che due numeri non abbiano nessun divisore comune se non l’£$ 1 $£. In questo caso diciamo che i due numeri sono primi tra loro o coprimi. Questo non vuol dire che sono due numeri primi, ma semplicemente che non hanno divisori in comune.
Esempio: £$ \text{M.C.D.}(15, 34) = 1 $£ perché scomponendo in fattori primi i due numeri, troviamo che £$ 15 = 3 \cdot 5 $£ e £$ 34 = 2 \cdot 17 $£. Vediamo che non ci sono divisori comuni, quindi il massimo, nonché l’unico divisore che hanno in comune, è l’£$ 1 $£.
Il M.C.D. è sempre diverso da £$ 0 $£ perché, come dovremmo avere ormai imparato, non possiamo dividere per £$ 0 $£.
Il minimo comune multiplo (m.c.m.)
Per i divisori può essere utile trovare il più grande comune a tutti. Per i multipli invece? Serve trovare il multiplo comune più grande o è meglio trovare il più piccolo?
Il minimo comune multiplo (m.c.m.) tra due (o più) numeri è il più piccolo tra tutti i multipli che hanno in comune.
Per trovare il minimo comune multiplo seguiamo un procedimento simile a quello che abbiamo imparato per il Massimo Comun Divisore:
- scomponiamo i numeri in fattori primi;
- moltiplichiamo i fattori comuni e non comuni prendendoli una volta sola, con l’esponente più grande.
Esempio: £$ \text{m.c.m.}(6, 15) = 30 $£ infatti se scomponiamo in fattori primi troviamo £$ 6 = 2 \cdot 3 $£ e £$ 15 = 3 \cdot 5 $£. Per trovare il m.c.m. scegliamo i fattori comuni e non comuni con l’esponente più grande, quindi £$ \text{m.c.m.}(6, 15) = 2 \cdot 3 \cdot 5 = 30 $£.
Non esistono numeri interi che hanno minimo comune multiplo uguale a £$ 1 $£. Però se due (o più) numeri sono primi tra loro, cioè con Massimo Comun Divisore uguale a £$ 1 $£, allora il minimo comune multiplo è uguale al prodotto tra i numeri.
Esempio: £$ 12 $£ e £$ 7 $£ sono primi tra loro perché £$ \text{M.C.D.}(12, 7) = 1 $£, quindi il £$ \text{m.c.m}(12, 7) = 12 \cdot 7 = 84 $£. Non esiste un multiplo più piccolo comune ad entrambi i numeri.
Proprietà e relazioni tra Massimo Comun Divisore e minimo comune multiplo
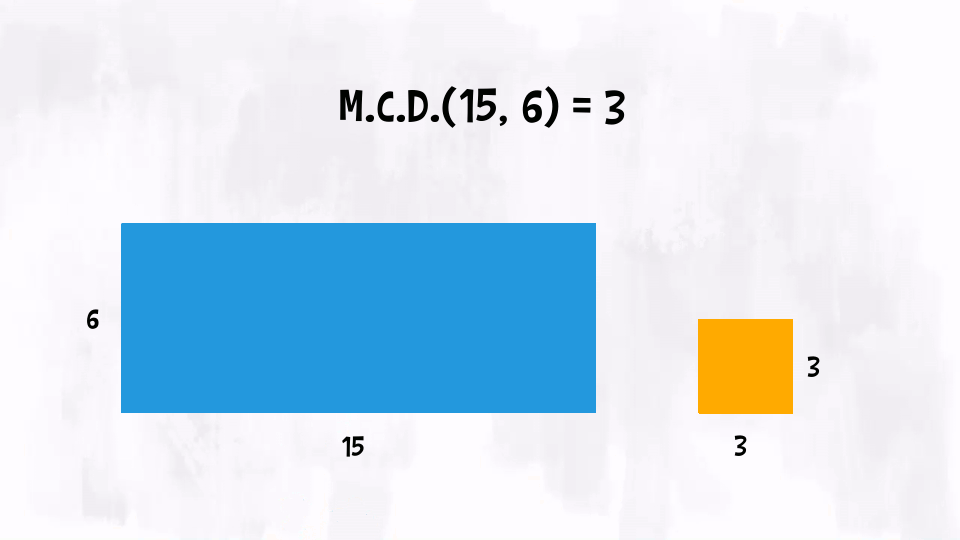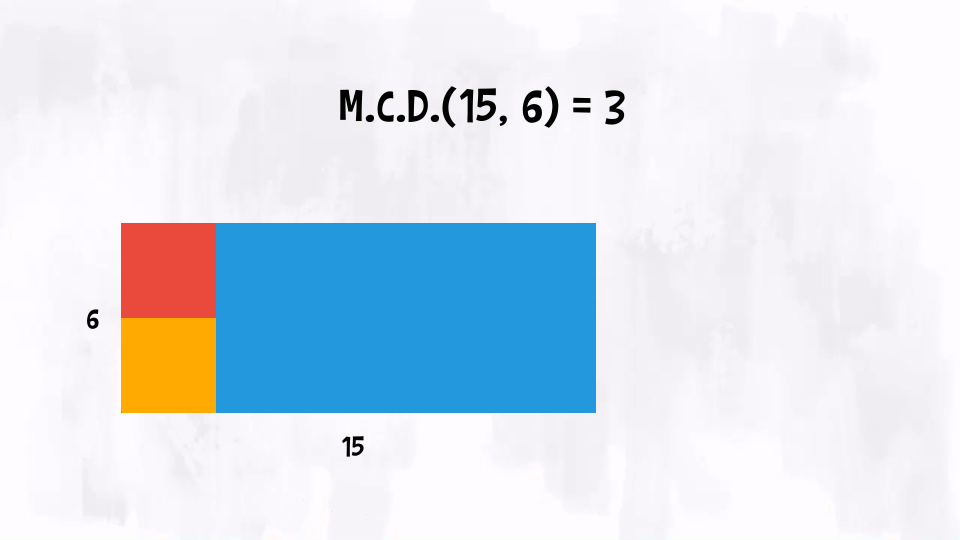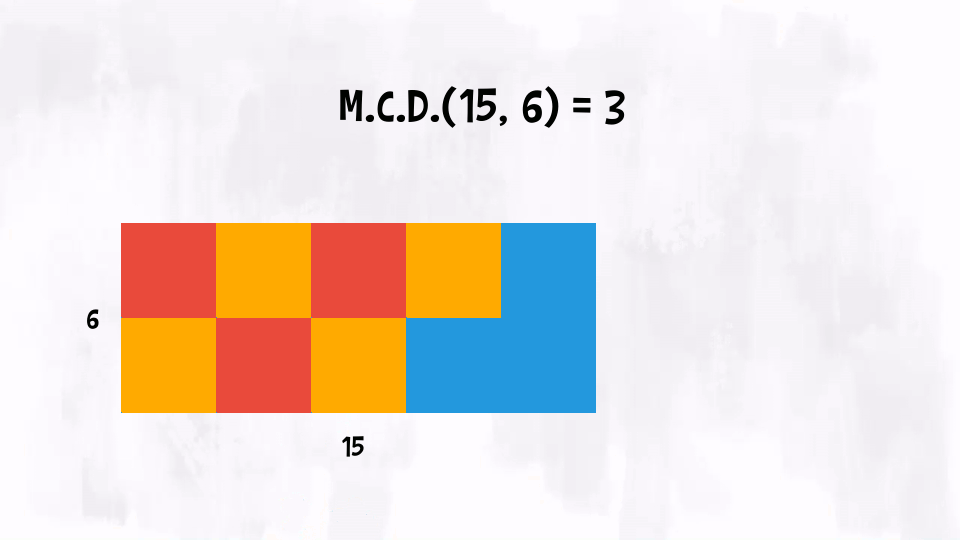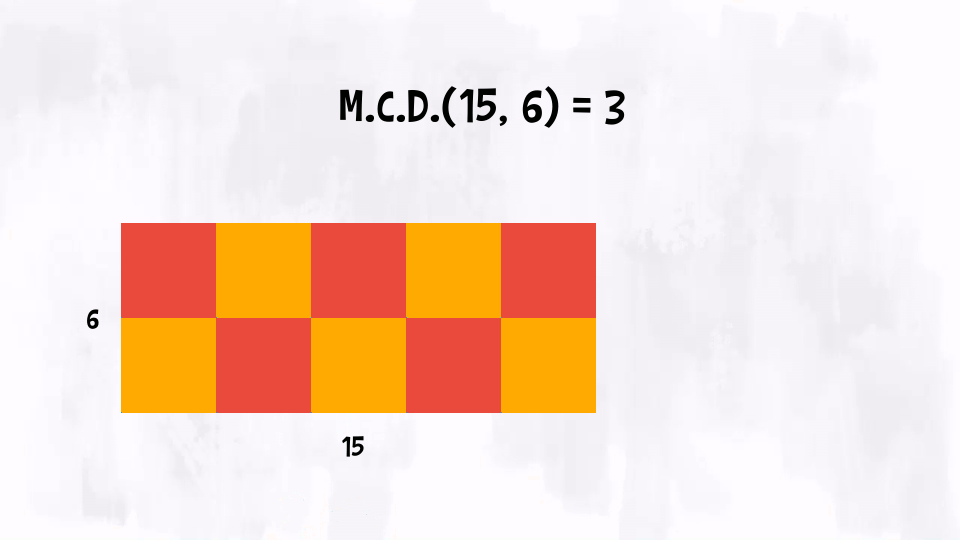
Proviamo a capire il Massimo Comun Divisore legandolo alla geometria. Prendiamo due numeri naturali, £$ a $£ e £$ b $£, e disegniamo un rettangolo che ha dimensioni £$ a \times b $£. Possiamo definire il £$ \text{M.C.D.}(a, b) $£ come il lato massimo del quadrato che può piastrellare il rettangolo.
Esempio: £$ \text{M.C.D.}(15, 6) = 3 $£, quindi, disegnato un rettangolo di dimensioni £$ 15 \times 6 $£ possiamo ricoprirlo con quadratini che hanno lato di lunghezza £$ 3 $£.
Il Massimo Comun Divisore e il minimo comune multiplo sono legati da alcune relazioni. Scopriamole!
Il prodotto tra il M.C.D. di due numeri e il m.c.m. degli stessi numeri è uguale al prodotto di questi due numeri.
Esempio: £$ \text{M.C.D.}(6, 32) \cdot \text{m.c.m.}(6, 32) = 2 \cdot 2^5 \cdot 3 = 96 $£. Questo risultato è proprio uguale al prodotto tra i due numeri di partenza, infatti £$ 32 \cdot 6 = 96 $£.
Ogni divisore comune a due numeri è anche divisore del loro M.C.D.. Ogni multiplo comune ai due numeri è divisibile per il loro minimo comune multiplo.
Calcoliamo il M.C.D. tra due numeri £$ a $£ e £$ b $£: se £$ a $£ è un divisore di £$ b $£, allora £$ a = \text{M.C.D.}(a, b) $£ e £$ b = \text{m.c.m.}(a, b) $£.
Esempio: consideriamo i due numeri £$ 7 $£ e £$ 35 $£. Con la scomposizione in fattori primi vediamo che £$ \text{M.C.D}(7, 35) = 7 $£ e £$ \text{m.c.m.}(7, 35) = 35 $£ perché il £$ 7 $£ è un divisore del £$ 35 $£.
Per calcolare il M.C.D. e il m.c.m. tra due numeri, utilizziamo la scomposizione in fattori primi e poi scegliamo i fattori comuni come abbiamo studiato. Ma, per velocizzare i calcoli, possiamo sfruttare la proprietà associativa: vale anche per calcolare il M.C.D. e il m.c.m..
Esempio: £$ \text{M.C.D.}(4, 12, 28) = \text{M.C.D.}(\text{M.C.D.}(4, 12), 28) = $£ £$ \text{M.C.D.}(4, \text{M.C.D.}(12, 28)) $£
£$ \text{m.c.m.}(4, 12, 28) = \text{m.c.m.}(\text{m.c.m.}(4, 12), 28) $£ £$ = \text{m.c.m.}(4, \text{m.c.m.}(12, 28)) $£
