Come si fa la moltiplicazione tra monomio e polinomio
La moltiplicazione tra un monomio e un polinomio è un’operazione fondamentale nell’ambito dell’algebra. Un monomio è un’espressione matematica costituita da un solo termine, che include un coefficiente e una o più variabili elevate a una certa potenza. Un polinomio, d’altro canto, è una somma di monomi. La moltiplicazione tra questi due enti si rivela una pratica essenziale per lo sviluppo di competenze algebriche più avanzate e per la risoluzione di problemi complessi.
Il processo di moltiplicazione si basa sull’applicazione del principio distributivo: il monomio viene moltiplicato per ogni termine del polinomio, uno alla volta. Questo significa che ogni termine del polinomio viene moltiplicato per il monomio, combinando i coefficienti e sommando gli esponenti delle variabili comuni. Il risultato è un nuovo polinomio, la cui complessità dipenderà dai gradi e dalle variabili dei termini originali.
Nell’articolo che segue, ci immergeremo in una guida dettagliata su come eseguire correttamente la moltiplicazione tra un monomio e un polinomio. Attraverso esempi pratici e spiegazioni chiare, miriamo a rendere questo concetto accessibile a tutti, dalla studentessa che affronta per la prima volta l’algebra al professionista che cerca di rinfrescare le proprie conoscenze.
Monomio per polinomio: come si fa la moltiplicazione
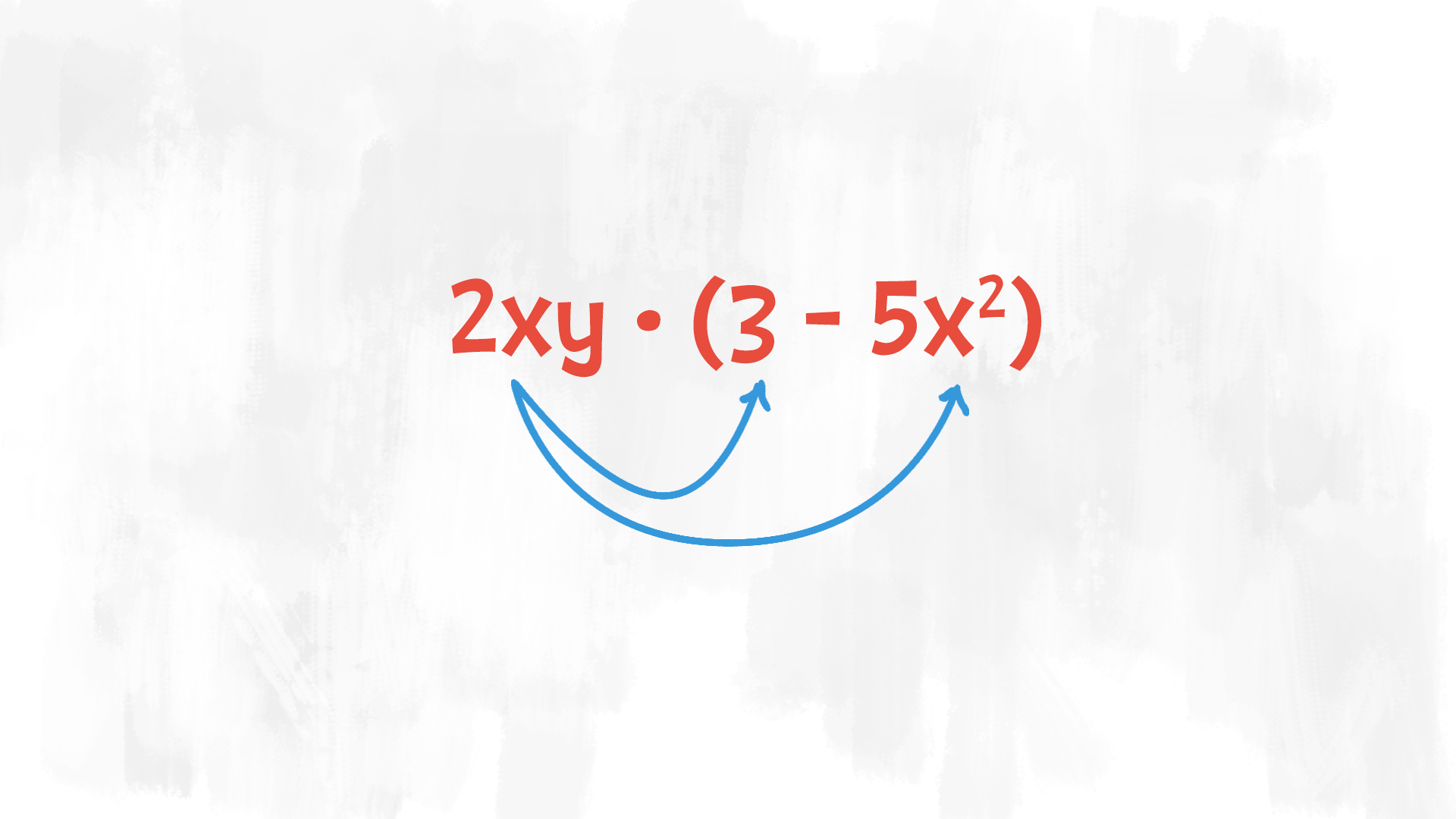
La moltiplicazione tra un monomio e un polinomio si svolge attraverso un processo relativamente semplice che sfrutta il principio distributivo. In pratica, il monomio viene moltiplicato per ciascun termine del polinomio, uno alla volta. Questo implica che il coefficiente del monomio viene moltiplicato per il coefficiente di ogni termine del polinomio, mentre le parti variabili si combinano seguendo le regole delle potenze.
Per eseguire questa operazione, si inizia prendendo il monomio e moltiplicandolo per il primo termine del polinomio. Successivamente, il risultato viene annotato e il monomio viene moltiplicato per il termine successivo del polinomio. Questo procedimento viene ripetuto fino a quando tutti i termini del polinomio sono stati moltiplicati per il monomio.
Un aspetto fondamentale da tenere in considerazione durante questo processo è la gestione degli esponenti quando si combinano le variabili. Se il monomio e un termine del polinomio contengono la stessa variabile, gli esponenti di questa variabile vengono sommati nel risultato della moltiplicazione.
Terminata la moltiplicazione di ogni termine, i risultati individuali vengono sommati per ottenere il polinomio finale. Questo risultato rappresenta il prodotto della moltiplicazione iniziale tra il monomio e il polinomio.
Iniziamo moltiplicando un monomio per un polinomio.
£$ 2xy \cdot (3 – 5x^2) $£
Utilizziamo la proprietà distributiva della moltiplicazione rispetto alla somma. La ricordi?
£$ 2 \cdot (3 + 5) = $£ £$2\cdot3 + 2\cdot 5$£
Allora “distribuiamo” il monomio su ciascun monomio del polinomio.
£$ (2xy \cdot 3) + (2xy\cdot(-5x^2)) $£
Eseguiamo la moltiplicazione tra monomi:
£$ (2\cdot3)xy + (2\cdot(-5)xyx^2) = \\ = 6xy – 10x^3y $£
