Prerequisiti per imparare a calcolare la radice di un numero
Prerequisiti per imparare a calcolare la radice di un numero:
Caricamento in corso...
Come calcolare la radice di un numero: scomposizione in fattori primi e tavole numeriche
Come calcolare la radice di un numero?
Non tutte le radici sono perfette: esistono numeri che non sono quadrati o cubi di un altro numero. In questi casi possiamo agire in due modi: con la scomposizione in fattori primi, oppure utilizzando le tavole numeriche.
Appunti
La radice quadrata è l'operazione inversa dell'elevamento al quadrato. La radice cubica è l'operazione inversa dell'elevamento al cubo. E possiamo andare avanti così per tutte le potenze. Ma come calcolare la radice quadrata di un numero che non è il quadrato di nessun numero intero?
Per esempio, come facciamo a calcolare £$\sqrt{54}$£ oppure £$\sqrt[3]{75}$£? Non sono radici perfette.
Quando dobbiamo calcolare la radice quadrata o cubica di un numero qualsiasi che non sia un quadrato o un cubo perfetto, puoi usare le tavole numeriche.
Altrimenti scomponi il numero in fattori primi e impara a portarli fuori dalla radice!
PREREQUISITI
Ripassa la scomposizione in fattori per provare a calcolare la radice quadrata di numeri che non sono quadrati perfetti: ripassa i divisori di un numero. Impara a portare i fattori fuori dalla radice con una divisione: sfrutta le proprietà delle potenze.
Contenuti di questa lezione su: Come calcolare la radice di un numero: scomposizione in fattori primi e tavole numeriche
Come calcolare la radice quadrata di quadrati non perfetti con le tavole numeriche
Come usare le tavole numeriche
Le tavole numeriche da 1 a 200
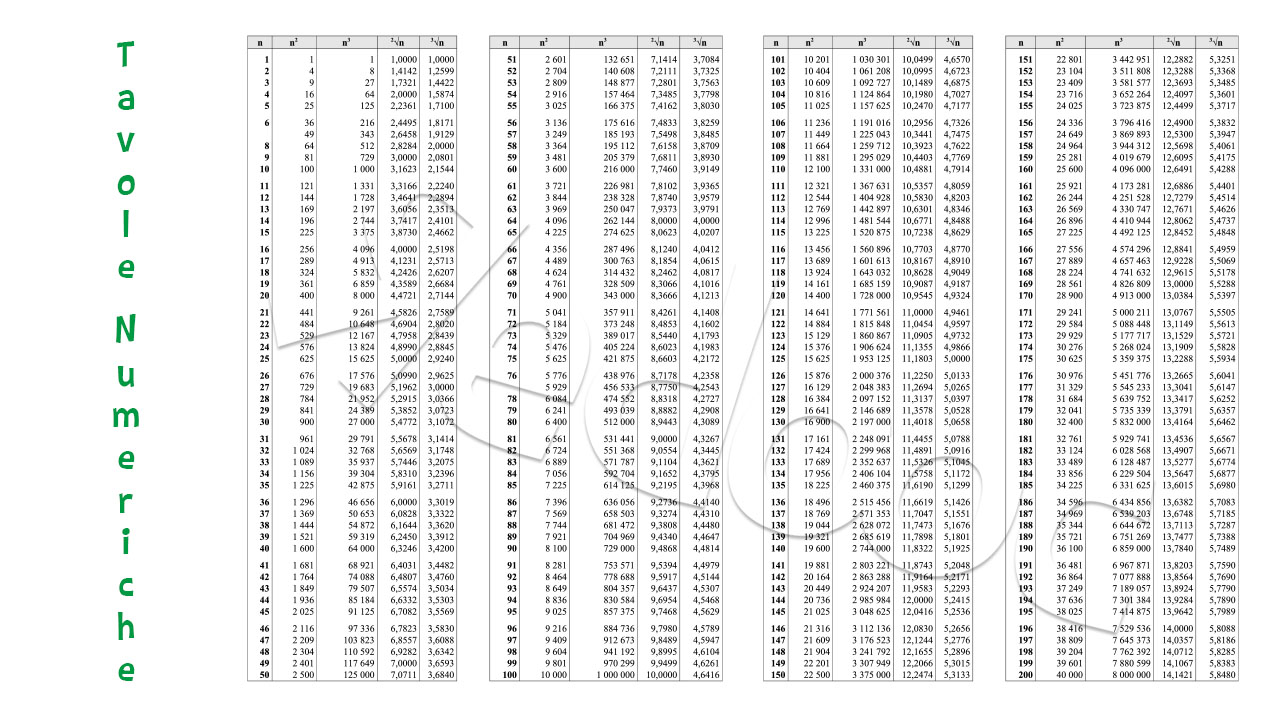
Abbiamo visto che è facile trovare la radice quadrata o cubica quando ci sono quadrati o cubi perfetti.
I numeri che terminano per £$ 2 $£, £$ 3 $£, £$ 7 $£, £$ 8 $£ o un numero dispari di £$0$£, sicuramente non sono quadrati perfetti. Come calcolare la radice quadrata di un numero che non sia un quadrato perfetto? E per le radici cubiche? Per trovare la radice quadrata o la radice cubica di quadrati e cubi non perfetti possiamo usare le tavole numeriche.
Le tavole numeriche sono delle tabelle in cui possiamo leggere il quadrato, il cubo, la radice quadrata e la radice cubica dei numeri da £$1$£ a £$1000$£.
Guarda il video per imparare ad usare le tavole numeriche!
Nella tabella delle radici quadrate, troviamo le radici approssimate alla quarta cifra dopo la virgola. Se i numeri non sono quadrati perfetti, dovremo approssimare per difetto o per eccesso alla cifra che ci interessa mantenere. Se la cifra subito dopo quella che ci interessa è minore di £$5$£, approssimiamo per difetto; se invece la cifra che ci interessa è compresa tra £$5$£ e £$9$£ (£$5 \le x \le 9$£), approssimiamo per eccesso.
Esempio:
- £$ \sqrt{5}=2,236067...$£ arrotondato al decimo è £$2,2$£. La seconda cifra dopo la virgola, cioè i centesimi, è £$3 < 5$£, quindi arrotondiamo per difetto, cioè lasciamo la cifra indicata: £$\sqrt{5}=2,2$£;
- £$\sqrt{5}=2,236067...$£ arrotondato al centesimo è £$2,24$£ La cifra dopo quella che ci interessa è £$6 > 5$£, quindi approssimiamo per eccesso, cioè aumentiamo di £$1$£ l’ultima cifra: £$\sqrt{5}=2,24$£.
Come calcolare le radici con la scomposizione in fattori primi
Calcolo della radice quadrata di un numero
Calcolo della radice cubica di un numero
Abbiamo visto che la radice è l'operazione inversa dell'elevamento a potenza. Abbiamo anche visto che è facile calcolare le radici perfette. Se non abbiamo una radice perfetta, ma dobbiamo calcolare la radice quadrata o cubica possiamo usare le tavole numeriche. In tutti gli altri casi?
In mancanza delle tavole numeriche o della calcolatrice, possiamo calcolare la radice di un numero utilizzando la scomposizione in fattori primi.
Partiamo dalla radice quadrata! Un numero è un quadrato perfetto se gli esponenti di tutti i fattori primi che troviamo dalla scomposizione sono pari. Possiamo “portare fuori” dalla radice tutti questi numeri dividendo l’esponente del radicando per l’indice di radice, cioè £$ 2 $£. Fuori dalla radice rimarrà lo stesso numero con esponente uguale al quoziente tra radicando e indice di radice. Dentro la radice rimane £$1$£, e visto che £$ \sqrt1 = 1 $£, possiamo anche non scriverla!
Esempio: £$\sqrt{900}=\sqrt{9 \cdot 100}=\sqrt{3^2 \cdot 5^2 \cdot 2^2}=3 \cdot 2 \cdot 5=30$£
Se il radicando non è un quadrato perfetto, una parte resterà sotto alla radice. In questo caso scomponi ulteriormente le potenze della fattorizzazione in un prodotto di potenze raggruppando le potenze con esponente pari e quelle con esponente dispari. Puoi portare fuori dalla radice quelle con esponente pari, e quindi divisibile per £$2$£, mentre le altre rimangono sotto la radice.
Esempio: £$ \sqrt{8}=\sqrt{2^3}= \sqrt{2^2 \cdot 2}=2\sqrt{2} $£ (due volte il radicale radice di £$2$£)
Questo procedimento ti permette di risolvere o semplificare ogni radice, basta scomporre il radicando come prodotto di numeri con esponente divisibile per l'indice della radice!
Esempio:
- £$\sqrt[3]{54}=\sqrt[3]{2 \cdot 3^3}=3\cdot \sqrt[3]{2}$£
- £$\sqrt[5]{2^6 \cdot 3^2 \cdot 4^{11}}=\sqrt[5]{2^5 \cdot 2 \cdot 3^2 \cdot 4^{10} \cdot 4} $£ £$ =2 \cdot 4^2 \cdot \sqrt[5]{2 \cdot 3^2 \cdot 4} $£
