Le proporzioni: cosa sono e come si risolvono
Le proporzioni in matematica sono delle relazioni che esprimono come due rapporti siano uguali l’uno all’altro. In altre parole, una proporzione è un’equazione che afferma che due rapporti o frazioni sono equivalenti. Una proporzione può essere scritta in vari modi, ma la forma più comune è quella di due frazioni uguali, come nell’esempio seguente:
$$\frac{a}{b} = \frac{c}{d} $$
Qui, £$a,b,c,d$£ sono numeri, e £$b,d$£ sono diversi da zero. La proporzione afferma che il rapporto tra £$a,b$£ è lo stesso del rapporto tra £$c, d$£.
Le proporzioni sono uno strumento potente in matematica e vengono utilizzate in una vasta gamma di applicazioni, dalla risoluzione di problemi nel quotidiano alla geometria, statistica e scienza. Ad esempio, possono essere usate per determinare un valore sconosciuto in un problema, come trovare una distanza su una mappa usando una scala, o per esprimere come due variabili siano collegate in un fenomeno scientifico o economico.
- Che cos'è una proporzione in matematica
- I termini della proporzione
- Qual è la proprietà fondamentale delle proporzioni
- Le proprietà fondamentali delle proporzioni
- La proporzionalità diretta e inversa
- Quando usiamo le proporzioni nella vita quotidiana
- Esercizi sulle proporzioni e sulle grandezze inversamente e direttamente proporzionali
Che cos’è una proporzione in matematica
Una proporzione è un’uguaglianza tra due rapporti equivalenti.
Esempio: £$2 : 5 = 54 : 135 $£ è una proporzione in cui uguagliamo il rapporto £$2 : 5$£ e il rapporto £$54 : 135$£. Infatti £$ \dfrac{54}{135} = \dfrac{6 \cdot 9}{ 15 \cdot 9} = \dfrac{2}{5}$£.
I due punti nei rapporti si leggono “sta a”, mentre l’uguale si legge “come”.
Quindi leggiamo la proporzione così: “£$2$£ sta a £$5$£ come £$54$£ sta a £$135$£“.
I termini della proporzione
Gli elementi della proporzione hanno dei nomi:
- i primi termini di ciascun rapporto sono gli antecedenti, i secondi termini invece sono i conseguenti.
Esempio: per la proporzione £$2 : 5 = 54 : 135$£ il £$2$£ ed il £$54$£ sono gli antecedenti, mentre il £$5$£ ed il £$135$£ sono i conseguenti. - I termini esterni della proporzione si chiamano estremi, mentre i termini interni si chiamano medi.
Esempio: per la proporzione £$2 : 5 = 54 : 135$£ il £$2$£ e il £$135$£ sono gli estremi, mentre il £$5$£ e il £$54$£ sono i medi.
Possiamo trovare rapporti tra grandezze omogenee e non omogenee. Quando svolgiamo una proporzione è importante che i due antecedenti si riferiscano entrambi alla parte (o viceversa al tutto) e che i due conseguenti si riferiscano entrambi al tutto (o viceversa alla parte).
Per esempio diciamo che il £$ 20\% $£ di £$ 80 $£ è uguale a £$ 16 $£ e possiamo scrivere questa proporzione: £$ 20 : 100 = 16 : 80 $£. Gli antecedenti sono £$ 20 $£ e £$ 16 $£ e rappresentano entrambi una parte del totale (che è scritto nei conseguenti, ed è il £$ 100 \% $£ oppure £$ 80 $£). Ma possiamo scrivere anche questa proporzione: £$ 100 : 20 = 80 : 16 $£. In questo caso, gli antecedenti rappresentano il tutto (£$ 100 \% $£ e £$ 80 $£), mentre i conseguenti sono la parte (£$ 20 \% $£ e £$ 16 $£).
Qual è la proprietà fondamentale delle proporzioni
La proprietà fondamentale delle proporzioni dice che il prodotto dei medi è uguale al prodotto degli estremi.
Esempio: £$2 : 5 = 54 : 135$£ troviamo quindi che £$5 \cdot 54 = 2 \cdot 135$£. Infatti £$ 5 \cdot 54 = 270 = 2 \cdot 135$£.
A cosa serve la proprietà fondamentale delle proporzioni? Possiamo usarla per verificare se una proporzione è corretta, cioè per controllare che sia un’uguaglianza tra due rapporti.
Esempio: £$2:5=3:15$£ non è una proporzione, infatti £$5 \cdot 3 =15 $£ che è diverso da £$ 2 \cdot 15=30$£.
Nel calcolo delle proporzioni, la proprietà fondamentale è più utile quando si deve calcolare un termine di una proporzione conoscendo gli altri £$ 3 $£. Se non conosci un valore della proporzione, chiamalo £$x$£. Per trovare il valore di £$x$£ applica la proprietà fondamentale e poi usa le formule inverse.
Esempio: £$5 : 400 = 2 : x$£ basta moltiplicare tra loro i medi e gli estremi, come dice la proprietà fondamentale. In questo modo troviamo £$400 \cdot 2 = 5 \cdot x$£, quindi per ricavare £$x$£, dobbiamo trovare quel numero che, moltiplicato per £$ 5 $£ dà £$ 800 $£, cioè £$ \frac{400 \cdot 2}{5} = x$£ che possiamo scrivere anche così: £$x = \frac{400 \cdot 2}{5}$£. Semplifichiamo il £$400$£ con il £$5$£ e troviamo che £$x = 80 \cdot 2 = 160$£.
Questo è quello che facciamo anche quando dobbiamo fare una torta per £$2$£ persone, ma nella ricetta ci sono le dosi per £$5$£ persone. Per trovare le dosi esatte, svolgi una proporzione! Facciamolo con la farina: per £$5$£ persone servono £$750 \text{ g}$£ di farina, per £$2$£ persone ne serviranno £$x$£, quindi scriviamo £$750:5=x:2$£. Applicando la proprietà fondamentale delle proporzioni troviamo £$5 \cdot x=750 \cdot 2 $£ allora £$ x=\frac{750 \cdot 2}{5}=300$£
Per £$2$£ persone bastano £$300 \text{ g}$£ di farina! Fai la proporzione con tutti gli ingredienti e la torta verrà perfetta!
Le proprietà fondamentali delle proporzioni
Le proporzioni matematiche hanno alcune proprietà che ci permettono di risolvere più velocemente gli esercizi.
Una proporzione è continua quando i due medi sono uguali tra loro.
Esempio: £$3 : 6 = 6 : 12$£ è una proporzione continua perché i medi sono entrambi uguali a £$6$£.
Oltre a quella fondamentale, le proporzioni hanno £$4$£ proprietà:
- Proprietà del permutare: una proporzione rimane valida se scambiamo tra loro i due medi o i due estremi.
Esempio: £$3 : 6 = 2 : 4$£ è equivalente a £$3 : 2 = 6 : 4$£ (scambiando i medi) che è equivalente a £$4 : 2 = 6 : 3$£ (scambiando gli estremi). - Proprietà dell’invertire: una proporzione rimane valida se scambiamo ciascun antecedente con il proprio conseguente.
Esempio: £$3 : 6 = 2 : 4$£ è equivalente a £$6 : 3 = 4 : 2$£. - Proprietà del comporre: la somma dei primi due termini sta a al primo (o al secondo) termine come la somma degli altri due termini sta al terzo (o al quarto) termine.
Esempio: £$3 : 6 = 2 : 4$£ è equivalente a £$(3 + 6) : 6 = (2 + 4) : 4$£ ed è equivalente a £$(3 + 6) : 3 = (2 + 4) : 2$£. - Proprietà dello scomporre: in una proporzione in cui gli antecedenti sono maggiori dei conseguenti, la differenza tra i primi due termini sta al primo (o al secondo) termine come la differenza tra il terzo e il quarto termine sta al terzo (o al quarto) termine.
Esempio: £$6 : 3 = 4 : 2$£ è equivalente a £$(6 – 3) : 3 = (4 – 2) : 2$£ ed è equivalente a £$(6 – 3) : 6 = (4 – 2) : 4$£.
Prova a dare un’occhiata alla nostra tabella che riassume tutti gli elementi chiave delle proprietà delle porzioni:

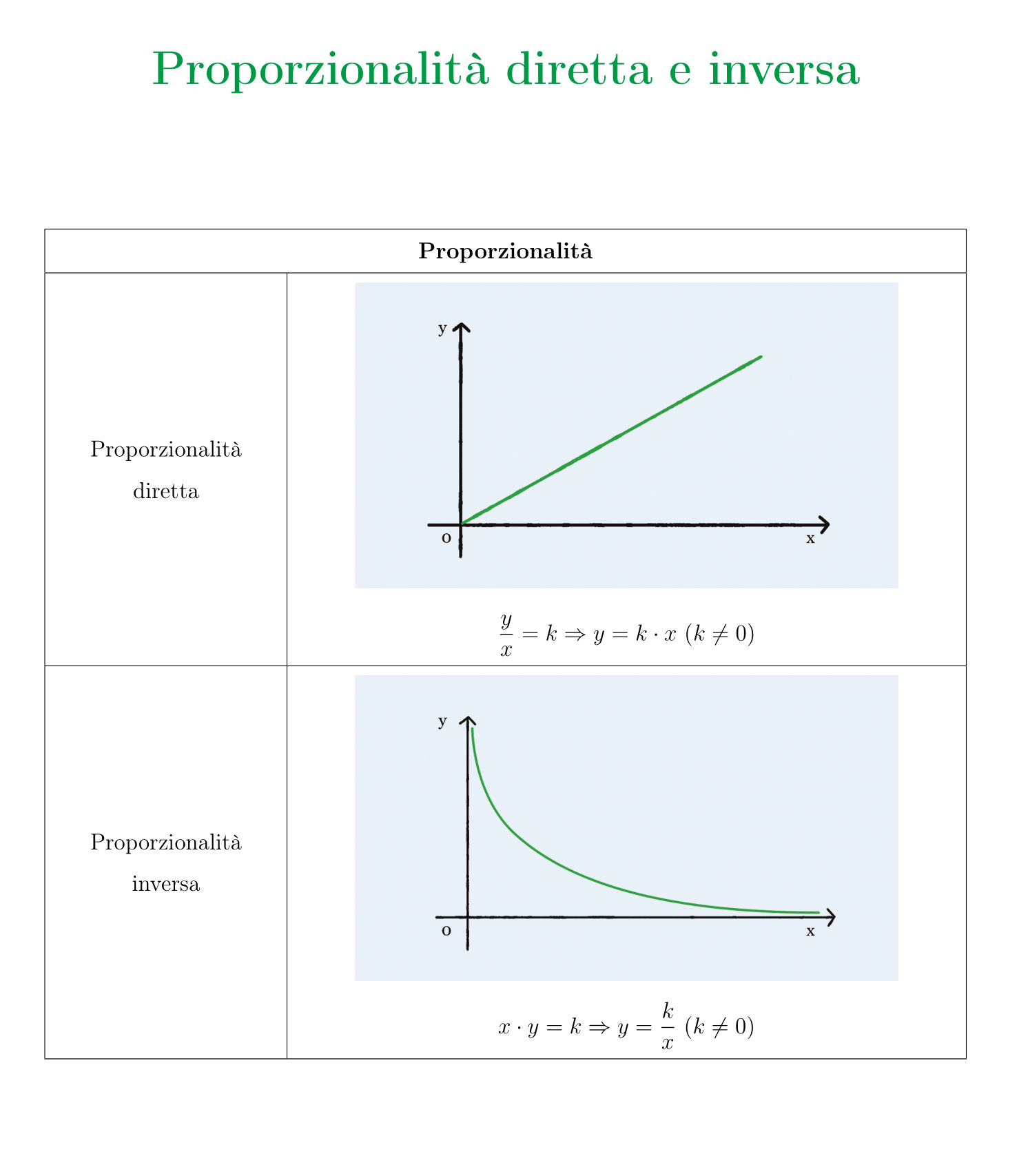
La proporzionalità diretta e inversa

Due grandezze £$x$£ e £$y$£ si definiscono direttamente proporzionali se il loro rapporto è sempre costante.
$$\dfrac{y}{x} = k \text{ allora } y = k · x \text{ con } k \ne 0$$
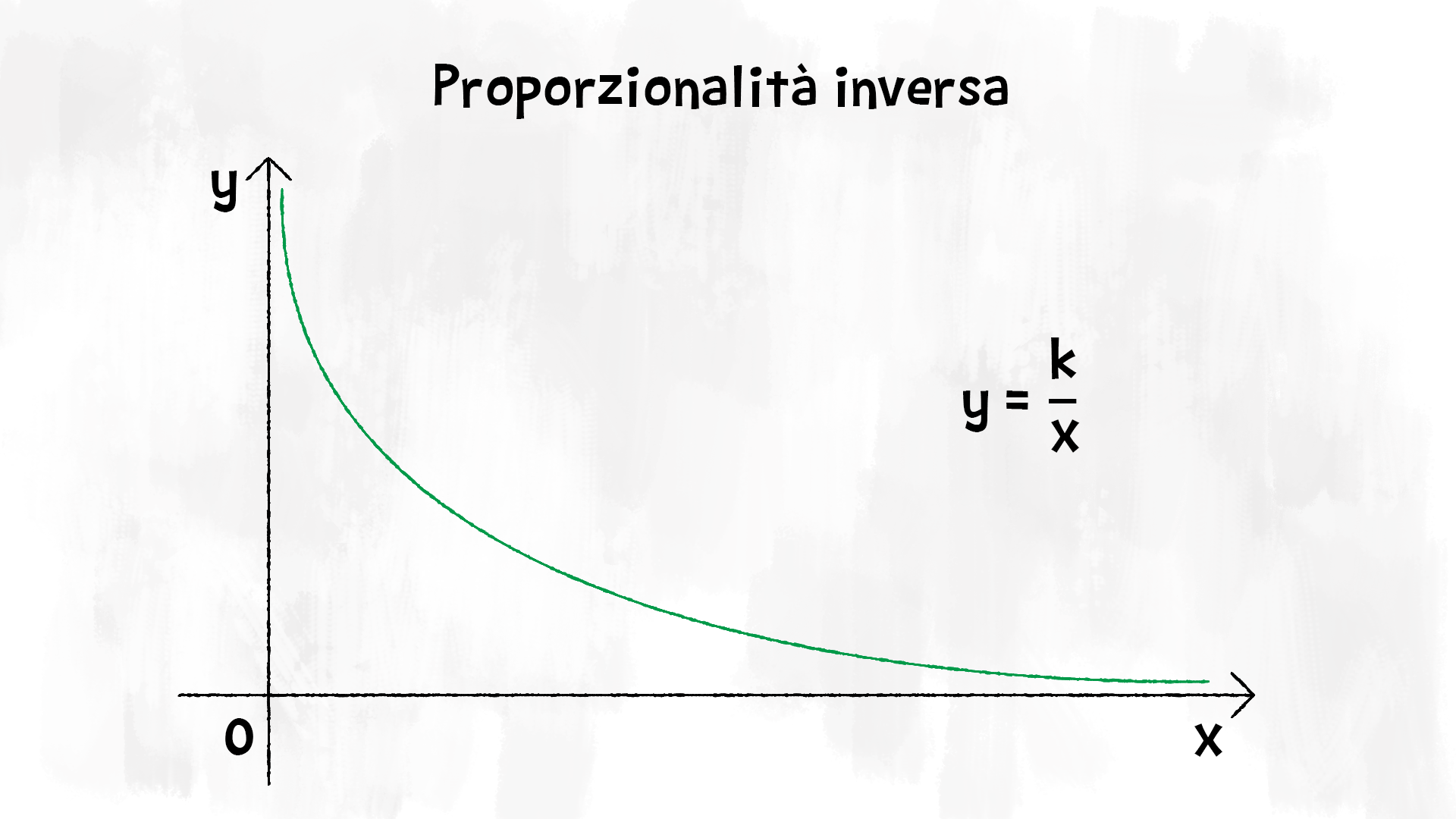
Due grandezze £$x$£ e £$y$£ si definiscono inversamente proporzionali se il loro prodotto rimane costante.
$$x · y = k \text{ allora } y = \dfrac{k}{x} \text{ con } k \ne 0 $$
Osserva la tabella qui sotto per ripassare!
Quando usiamo le proporzioni nella vita quotidiana
Le proporzioni sono molto utili quando devi fare una torta oppure quando ci sono i saldi!
Perché sono utili nei saldi? Un modo per calcolare i prezzi scontati è quello di utilizzare le
proporzioni. Vorresti un vestito che costa £$135 \ € $£ a prezzo pieno e vuoi calcolare quanto spenderesti in meno con il £$30 \%$£ di sconto.
Chiamiamo £$x$£ il risparmio, in denaro. La proporzione da risolvere è:
£$30:100=x:135$£, cioè lo sconto percentuale (£$ 30\% $£) sta alla percentuale totale (£$100 \% $£)
come il risparmio sta al costo del vestito (£$ 135 \ € $£). Applichiamo la proprietà fondamentale delle proporzioni e troviamo: £$100 \cdot x= 30 \cdot 135$£, quindi £$x=\frac{30 \cdot 135}{100}=40,5$£. Risparmieresti £$40, 5 \ €$£, quindi spenderesti £$135-40,5=94,5 \ €$£.
Abbiamo così usato le proporzioni per calcolare una percentuale!
Perché sono utili quando prepariamo le torte? Possono esserci utili quando facciamo una torta. La ricetta dice che per £$8$£ persone servono £$1000 \text{ g}$£ di farina, £$350 \text{ g}$£ di zucchero, £$1 \text{ l}$£ di latte, un pizzico di sale e un baccello di vaniglia! Tu hai invitato solo £$3$£ persone e non vuoi che avanzi della torta. Quale sarà la tua ricetta? La troverai facendo le proporzioni per tutti gli ingredienti:
- Farina: £$1000: 8=x:3$£ quindi £$x=\frac{1000 \cdot 3}{8}=375$£. Ti serviranno £$375 \text{ g}$£ di farina!
- Zucchero: £$350:8=x:3$£ quindi £$ x=\frac{350 \cdot 3}{8}=131,25$£ Ti serviranno £$132 \text{ g}$£ di zucchero, sempre meglio arrotondare per eccesso!
- Latte: £$1\text{ l}=1000 \text{ ml}$£, facciamo la proporzione in £$ \text{ml}$£ che è più comodo! £$1000:8=x:3$£, che è la stessa proporzione della farina, quindi ti serviranno £$375 \text{ ml}$£ di latte!
- Vaniglia: £$1:8=x:3$£ quindi £$x=\frac{3}{8}$£. Dividi il baccello di vaniglia in £$8 $£ parti e usane £$3$£!
- Sale… Beh, un po’ meno di un pizzico dovrebbe bastare!
Esercizi sulle proporzioni e sulle grandezze inversamente e direttamente proporzionali
Se ne hai bisogno, scarica il pdf con gli esercizi qui!






