Prerequisiti per imparare il prodotto cartesiano
Prerequisiti per imparare il prodotto cartesiano:
Caricamento in corso...
Il prodotto cartesiano
Ora che hai imparato come fare unione e intersezione di insiemi, scopri una nuova operazione tra insiemi: il prodotto cartesiano. Come funziona? E come si rappresenta? Dove hai già sentito l'aggettivo cartesiano? Scopri i legami tra prodotto cartesiano e piano cartesiano.
Appunti
Possiamo dire che l'unione di insiemi è come un'addizione. L'intersezione tra insiemi è un'operazione che permette di trovare gli elementi che gli insiemi hanno in comune. Esiste anche la moltiplicazione tra insiemi? Più o meno sì, è il prodotto cartesiano.
In questa lezione imparerai che operazione è il prodotto cartesiano: gli elementi che fanno parte dell'insieme prodotto cartesiano, non sono elementi singoli, ma sono coppie. Esistono diversi modi per rappresentare il prodotto cartesiano: oltre al diagramma a frecce c'è anche la rappresentazione in tabella o il diagramma cartesiano.
Scopri tutto su questa nuova operazione e mettiti alla prova con gli esercizi svolti!
Contenuti di questa lezione su: Il prodotto cartesiano
Ordiniamo un pranzo con il prodotto cartesiano
Abbiamo imparato come fare unione e intersezione tra due insiemi. Ma esiste un’altra operazione. Come per i numeri, possiamo fare anche la moltiplicazione tra insiemi attraverso il prodotto cartesiano.
Indichiamo questa operazione con un simbolo che ricorda molto quello che utilizziamo per la moltiplicazione tra numeri: £$ \times $£.
Prendiamo due insiemi £$ A $£ e £$ B $£.
Il prodotto cartesiano è l’insieme di tutte le coppie £$ (a; b) $£ con £$ a \in A $£ e £$ b \in B $£. L’insieme di queste coppie è l’insieme £$ A \times B $£ e contiene un numero di elementi pari al prodotto del numero di elementi di £$ A $£ per il numero di elementi di £$ B$£.
Diciamo che la cardinalità - la cardinalità è il numero di elementi di un insieme - dell'insieme prodotto cartesiano è uguale al prodotto delle cardinalità dei due insiemi di partenza.
Esempio:
£$ A = \{ 1,2,3 \} $£ e £$ B = \{2,3 \} $£. Allora il prodotto cartesiano è l'insieme
$$ A \times B = \{ (1;2), (1; 3), (2;2), (2;3), (3; 2), (3;3) \} $$
Questo insieme contiene 6 elementi, che è proprio uguale al prodotto dei 3 elementi di £$ A $£ per i 2 elementi di £$ B $£.
Gli elementi del prodotto cartesiano sono coppie ordinate. È importante l’ordine degli elementi nella coppia: infatti £$ (2; 3) \ne (3; 2) $£. Dobbiamo inserire entrambe le coppie nell’insieme prodotto, una non esclude l’altra: coppie diverse forniscono informazioni diverse.
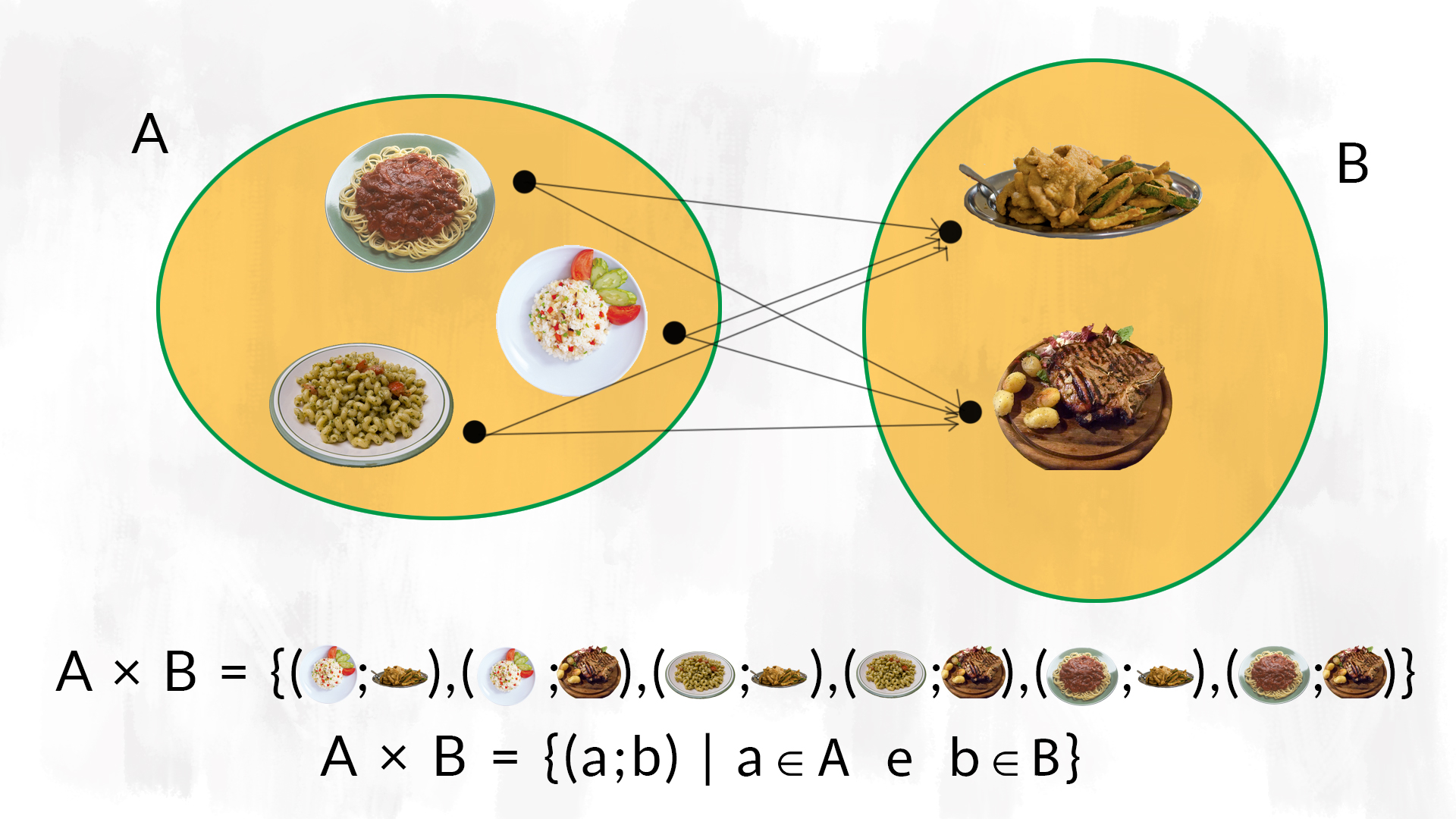
Nell'immagine vediamo il prodotto cartesiano tra due insiemi, uno che contiene dei primi piatti e uno che contiene dei secondi piatti. Si capisce bene che il prodotto cartesiano è l'insieme di tutti i possibili menu che possiamo scegliere componendo le diverse pietanze. Ogni volta che esci a pranzo, fai un prodotto cartesiano. Incredibile, vero?
Trovi la tabella con tutte le formule qui.
Come rappresentare il prodotto cartesiano
Tabella a doppia entrata
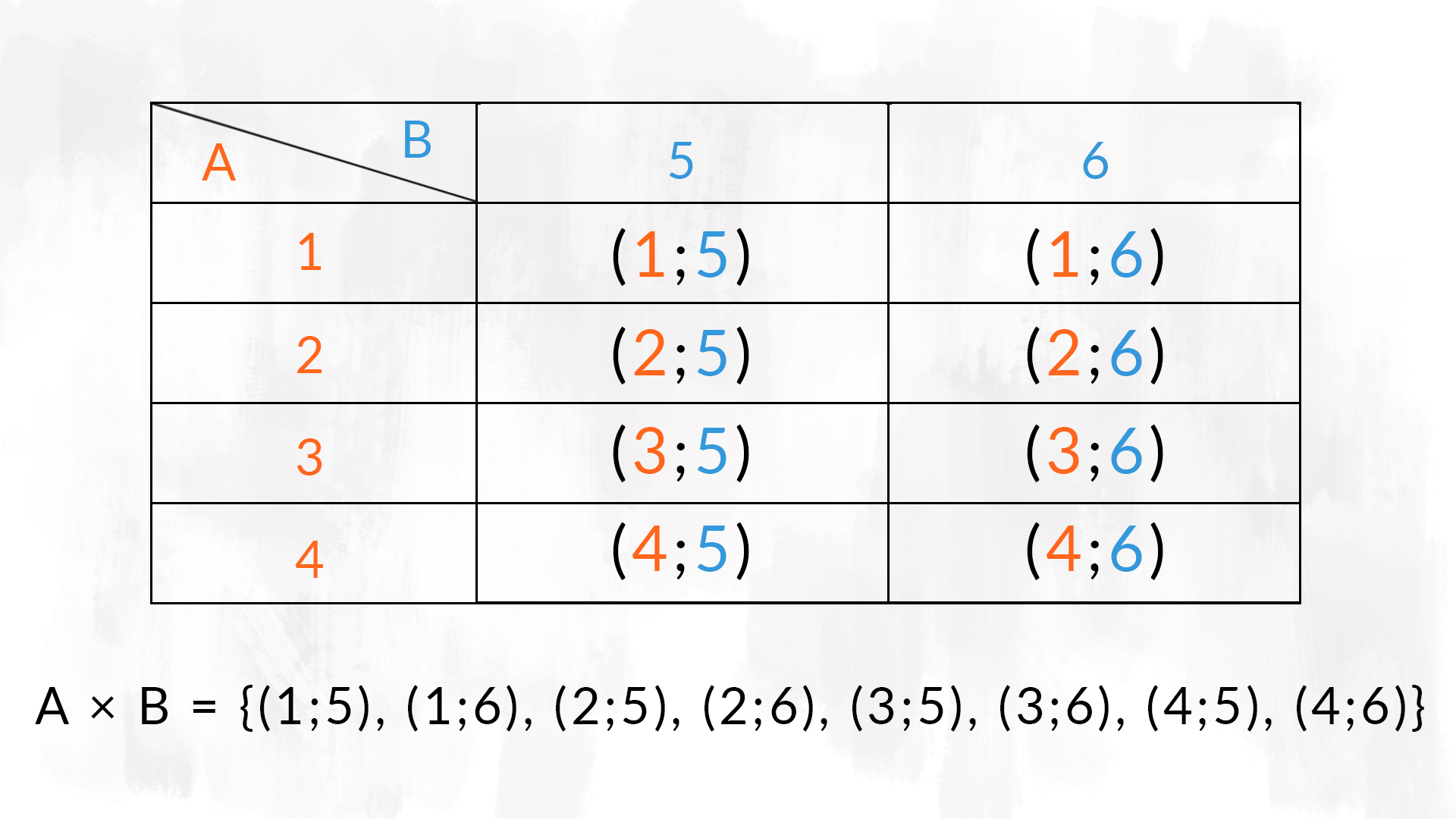
Diagramma cartesiano
Esistono diversi modi per rappresentare questa operazione tra insiemi. Corrispondono in parte a quelli che abbiamo già visto per gli insiemi e nell'esempio del primo post:
- rappresentazione con un diagramma a frecce: il prodotto cartesiano è rappresentato dalle frecce che collegano ciascun elemento del primo insieme a ciascun elemento del secondo insieme;
- rappresentazione per elencazione: elenchiamo tutte le coppie che si formano con il prodotto cartesiano;
- rappresentazione per caratteristica: per definizione, l’insieme £$ A \times B $£ è l’insieme delle coppie di elementi tali che il primo appartiene all’insieme £$ A $£ e il secondo appartiene all’insieme £$ B $£, cioè, scritto in linguaggio matematico, $$ A \times B = \{ (a; b) | a \in A, b \in B \} $$
Qual è la novità quindi? Esistono altri modi più intuitivi per rappresentare questa operazione:
- la tabella a doppia entrata: costruiamo una tabella in cui inseriamo gli elementi dei due insiemi e quindi le coppie che si formano con il prodotto cartesiano;
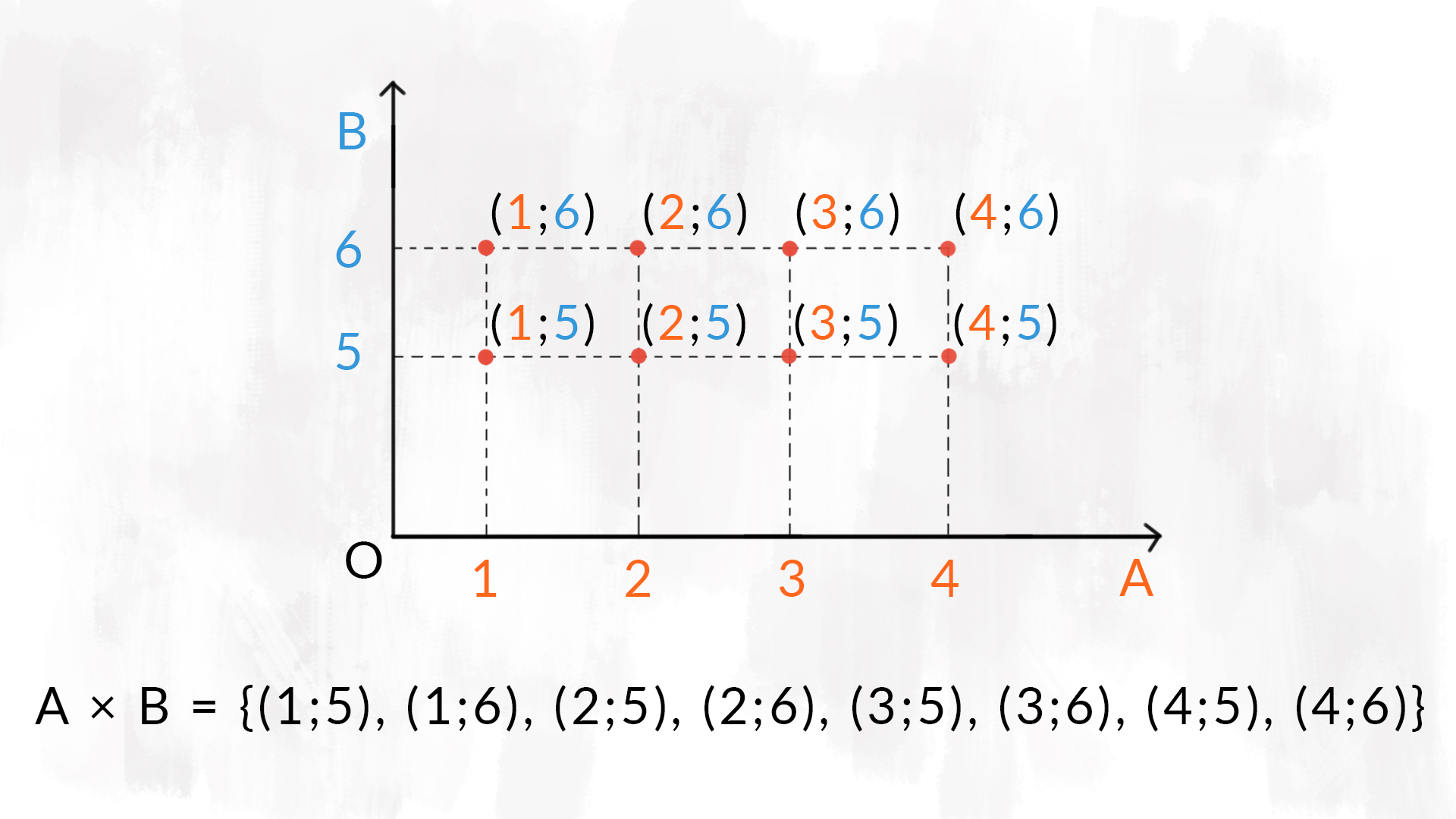
- il diagramma cartesiano: sicuramente il termine cartesiano ti fa tornare in mente il piano cartesiano. Infatti è proprio quello che utilizziamo per questa rappresentazione: posizioniamo sull’asse delle £$ x $£ gli elementi del primo insieme e sull’asse delle £$ y $£ quelli del secondo insieme. Il prodotto cartesiano individua dei punti sul piano cartesiano: possiamo infatti vedere le coppie di elementi come le coordinate dei punti sul piano. Ecco l’importanza dell’ordine degli elementi nelle coppie: il punto £$ (2;3) $£ è diverso dal punto £$ (3; 2) $£.
Osserva nelle immagini i differenti modi per rappresentare il prodotto cartesiano tra gli insiemi £$ A = \{ 1,2,3,4 \} $£ e £$ B = \{5, 6 \} $£.
Proprietà del prodotto cartesiano
Il prodotto tra insiemi è un’operazione simile al prodotto tra numeri. Vediamo alcuni casi particolari.
Cosa succede se dobbiamo trovare il prodotto cartesiano tra un insieme e se stesso? Consideriamo l’insieme £$ A = \{ a, b \} $£ e cerchiamo l‘insieme £$ A \times A $£: funziona esattamente come con i numeri! Stiamo calcolando il quadrato di un insieme. Infatti:
$$ A \times A = A^2 = \{ (a;a), (a;b), (b;a), (b;b) \} $$
Che insieme è il prodotto cartesiano tra un insieme £$ A = \{a,b \} $£ e l’insieme vuoto £$ \varnothing $£? Anche in questo caso funziona come per i numeri. Il risultato di questo prodotto è analogo al risultato del prodotto di un numero per £$ 0 $£, cioè è uguale allo zero degli insiemi.
$$ A \times \varnothing = \varnothing $$
Per il prodotto cartesiano non vale la proprietà commutativa: infatti le coppie che si formano con il prodotto cartesiano, sono coppie ordinate di elementi. Invertendo l’ordine dei due insiemi, abbiamo delle coppie diverse.
$$ A \times B \ne B \times A $$
Valgono poi delle altre proprietà particolari, riconducibili alla proprietà distributiva che abbiamo studiato per i numeri. Le vediamo velocemente:
- £$ A \times (B \cup C) = (A \times B) \cup (A \times C) $£
- analogamente £$ ( A \cup B) \times C = (A \times C) \cup (B \times C) $£
- £$ A \times (B \cap C) = (A \times B) \cap (A \times C) $£
- analogamente £$ ( A \cap B) \times C = (A \times C) \cap (B \times C) $£
