Le funzioni matematiche: definizione e proprietà
Le funzioni in matematica sono concetti fondamentali che descrivono una relazione speciale tra insiemi di numeri o altri oggetti. In termini semplici, una funzione è una regola che associa ogni elemento di un insieme, detto dominio, con un unico elemento di un altro insieme, chiamato codominio.
Per comprendere meglio, immagina una macchina che per ogni input produce un output specifico. In una funzione matematica, l’input è un elemento del dominio, e l’output è l’elemento del codominio associato a quell’input dalla “regola” della funzione. Questa regola può essere espressa in vari modi, come una formula, un grafico, o una descrizione verbale.
Le funzioni sono utilizzate per descrivere relazioni matematiche, risolvere equazioni, modellare fenomeni fisici, economici, biologici, e molto altro. Le funzioni possono assumere forme molto diverse, da semplici linee rette (funzioni lineari) a curve complesse (come le funzioni esponenziali o logaritmiche).
Inoltre, lo studio delle funzioni include l’analisi del loro comportamento, come il calcolo di limiti, derivate e integrali in calcolo differenziale e integrale. Questo permette di esplorare come le funzioni cambiano, come crescono o decrescono, e come si comportano in punti specifici o su intervalli.
Capiamo insieme cosa sono più nel dettaglio.
- Cos'è una funzione in matematica
- Cos'è una funzione y=f(x): definizione
- Esempi di funzioni che non sapevi di conoscere
- Le proprietà delle funzioni
- Ripassa per l'interrogazione sulle funzioni
Cos’è una funzione in matematica
Hai mai provato a fare una spremuta d’arance? O un frullato di frutta? A partire dal frutto, otteniamo un buon frullato attraverso il frullatore. I frutti sono l’input, cioè il nostro punto di partenza, il frullato è l’output, cioè il risultato.
Una funzione, quindi, è come un frullatore! È uno strumento che prende un input, lo “lavora” e trova l’output corrispondente. Ad ogni input corrisponde un unico output! Non è possibile che a due output diversi corrisponda uno stesso input. Tornando al nostro esempio, con una banana non possiamo ottenere un frullato di banana e, contemporaneamente un frullato di fragola. Ad ogni frutto corrisponde il suo frullato!
La caratteristica di una funzione è proprio questa: un solo input, non potrà mai dare due output diversi. A risultati diversi, corrispondono elementi di partenza diversi.
Cos’è una funzione y=f(x): definizione
Abbiamo detto che una funzione prende un input in ingresso e dà un output come risultato. Una funzione mette in corrispondenza due insiemi di valori o di oggetti.
Proviamo a dirlo in termini più matematici, indicando la funzione con una lettera in corsivo minuscolo. Consideriamo un insieme £$ X $£ e un insieme £$ Y $£. Preso £$ x \in X $£ e £$ y \in Y $£ diciamo che £$ y $£ è funzione di £$ x $£ se esiste una funzione £$ f $£ tale che
$$ y = f(x) $$
La funzione £$ f $£ associa ad ogni elemento di £$ X $£ un unico elemento di £$ Y $£.
Quanto abbiamo scritto sopra è solo un’abbreviazione della scrittura £$ \text{funzione}(\text{input}) = \text{output} $£. La funzione è come una macchina che prende qualcosa e lo trasforma in un’altra cosa.
La £$ x $£ si chiama variabile indipendente, mentre la £$ y $£ è la variabile dipendente. Infatti il valore di £$ y $£ dipende dal valore di £$ x $£.
L’insieme £$ X $£ è il dominio della funzione £$ f $£, cioè l’insieme di partenza, l’insieme che contiene gli “input” per la funzione. L’insieme £$ Y $£, invece, è il codominio, cioè l’insieme che contiene tutti gli “output” della funzione £$ f $£. Fanno parte del codominio tutti gli elementi tali che £$ y = f(x) $£.
Esempi di funzioni che non sapevi di conoscere
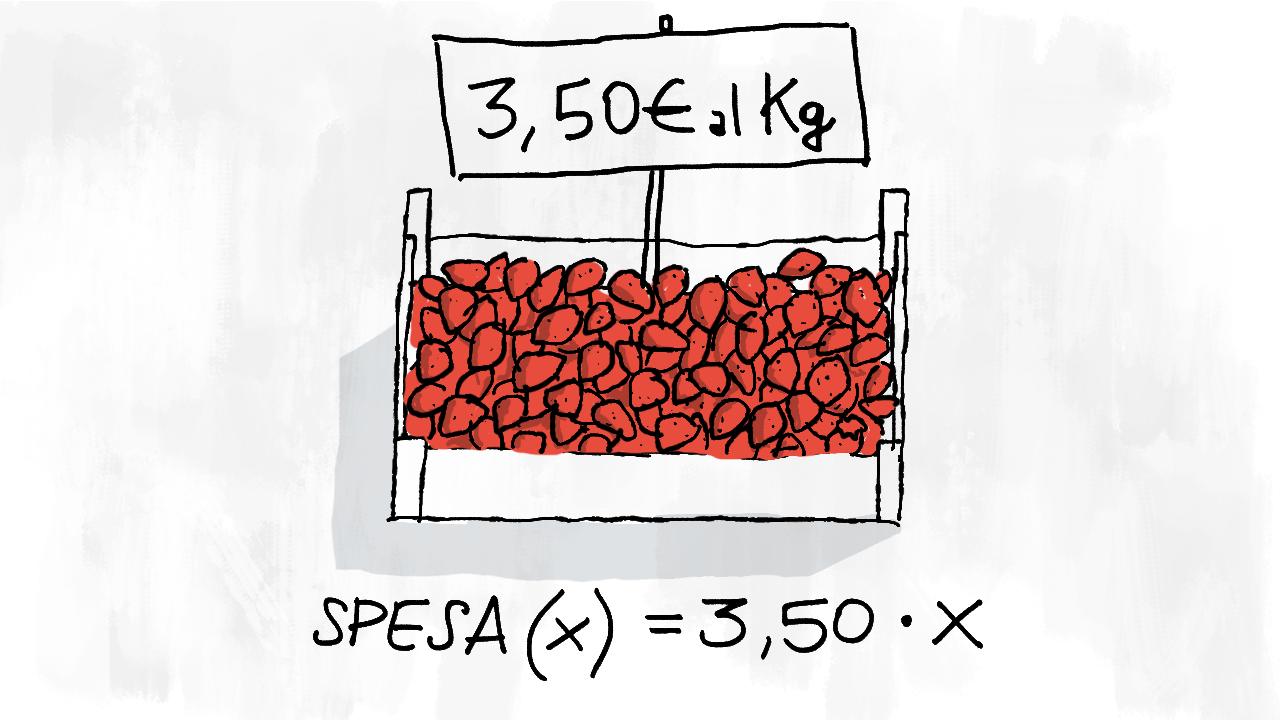
A far la spesa di funzioni
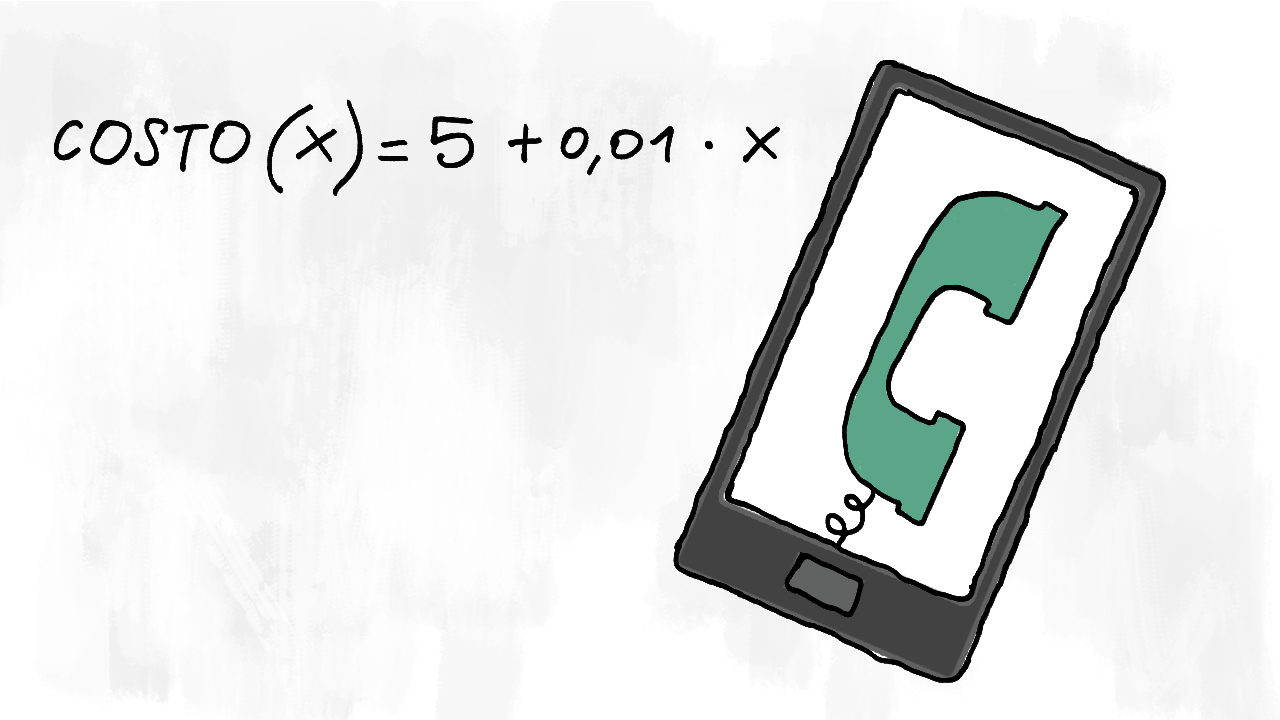
La funzione tariffa telefonica
Ma a cosa servono mai queste funzioni? Le abbiamo mai incontrate nella vita di tutti i giorni? Certo! Pensa a quando vai a fare la spesa: nel reparto ortofrutta tutti i prezzi sono al chilo. La spesa totale è una funzione della quantità di frutta che stiamo comprando. È un’equazione!
Esempio: le fragole costano £$ 3,50 $£ € al chilo. Possiamo scrivere la funzione £$ s $£ della spesa in questo modo: £$ s(x) = 3,5 \cdot x $£ dove indichiamo con £$ x $£ la quantità di fragole che compriamo in chilogrammi.
Se prendiamo £$ 1 \text{ kg} $£ di fragole, la nostra spesa sarà £$ s(1) = 3,50 \cdot 1 = 3,5 $£ €.
Se prendiamo £$ 350 \text{ g} = 0,35 \text{ kg} $£ di fragola, la nostra spesa sarà £$ s(0,35) = 3,50 \cdot 0,35 = 1,225 $£ €. Ma non esistono i millesimi di euro, quindi probabilmente spenderemo £$ 1,23 $£ €.
Con questo esempio abbiamo visto come calcolare il valore di una funzione per un determinato valore. Cioè abbiamo imparato a valutare la funzione in un punto.
Vediamo un altro esempio per entrare nel mondo delle funzioni.
Esempio: la tua tariffa telefonica ha un costo di £$ 5 $£ € al mese, a cui però va ad aggiungersi un costo di £$ 0,01 $£ € per ogni minuto di chiamata (questa tariffa fa in modo che chiamando per 30 secondi, spenderai comunque 1 centesimo; chiamando per 1 minuto e 50 secondi, spenderai comunque 2 centesimi). Qual è la funzione che rappresenta la tua spesa mensile?
Chiamiamo la funzione £$ c $£ e indichiamo con la variabile indipendente £$ x $£ i minuti (interi arrotondati per eccesso) di chiamate. La nostra spesa mensile sarà indicata dalla funzione £$ c(x) = 5 + 0,01 \cdot x $£.
Se in un mese facciamo chiamate per 7 minuti, spenderemo £$ c(7) = 5 + 0,01 \cdot 7 = 5,07 $£ €.
Se in un mese facciamo chiamate per 15 minuti e 42 secondi, spenderemo come se avessimo chiamato per 16 minuti, cioè £$ c(16) = 5 + 0,01 \cdot 16 = 5,16 $£ €.
Le proprietà delle funzioni
Conoscere le proprietà delle funzioni permette di fare meno calcoli e uno studio di funzione più veloce e semplice.
Possiamo capire se una funzione ha una determinata proprietà attraverso lo studio analitico della funzione (facendo cioè i calcoli) oppure attraverso il grafico (se già lo abbiamo). Tra le varie proprietà di una funzione abbiamo:
- funzioni iniettive, suriettive, biunivoche: le funzioni hanno delle proprietà che possiamo usare per studiarle meglio e più velocemente,
- funzioni crescenti e decrescenti: lo studio degli intervalli di monotonia della funzione è importante per capirne il comportamento,
- funzioni pari e dispari: alcune funzioni possono essere simmetriche rispetto all’asse y (funzione pari) oppure rispetto all’origine degli assi (funzione dispari).
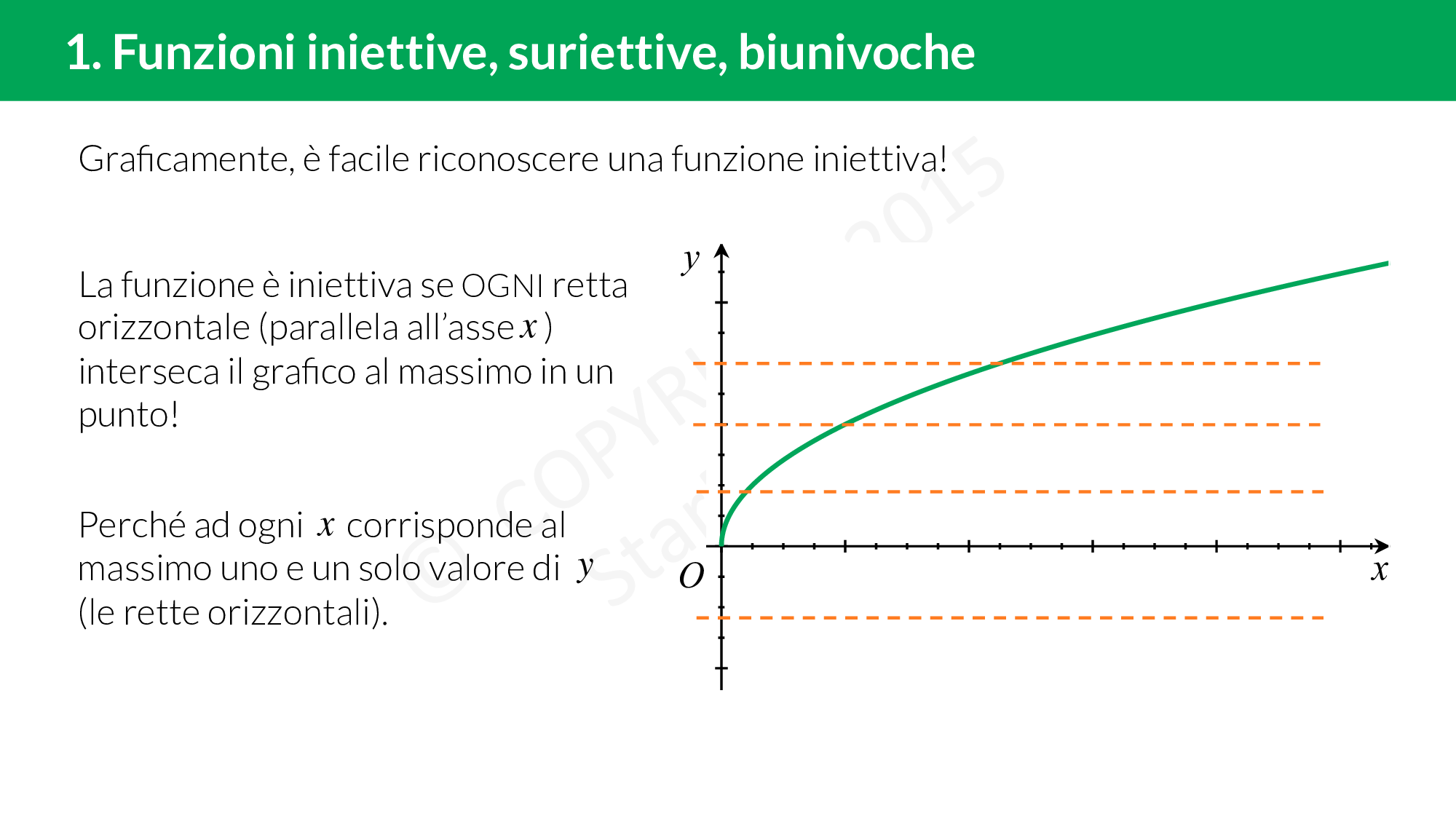
Iniettive, suriettive, biunivoche
Funzioni e proprietà: iniettive, suriettive, biunivoche, crescenti, decrescenti - Galleria
Una funzione può essere iniettiva, suriettiva oppure tutt’e due. In questo caso diciamo che la funzione è biunivoca. Attenzione però: una funzione può non essere né iniettiva né suriettiva. Una funzione è:
- iniettiva se OGNI elemento del codominio è immagine di un solo elemento del dominio;
- suriettiva se il codominio coincide con l’insieme di arrivo;
- biunivoca se è iniettiva e suriettiva.
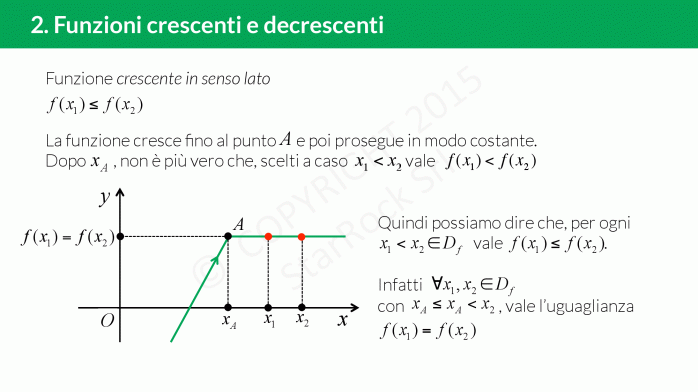
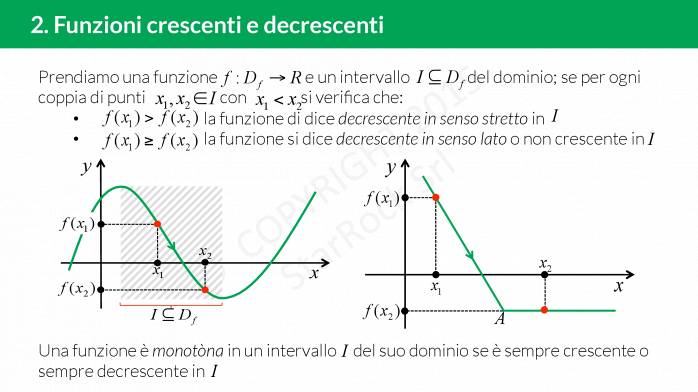
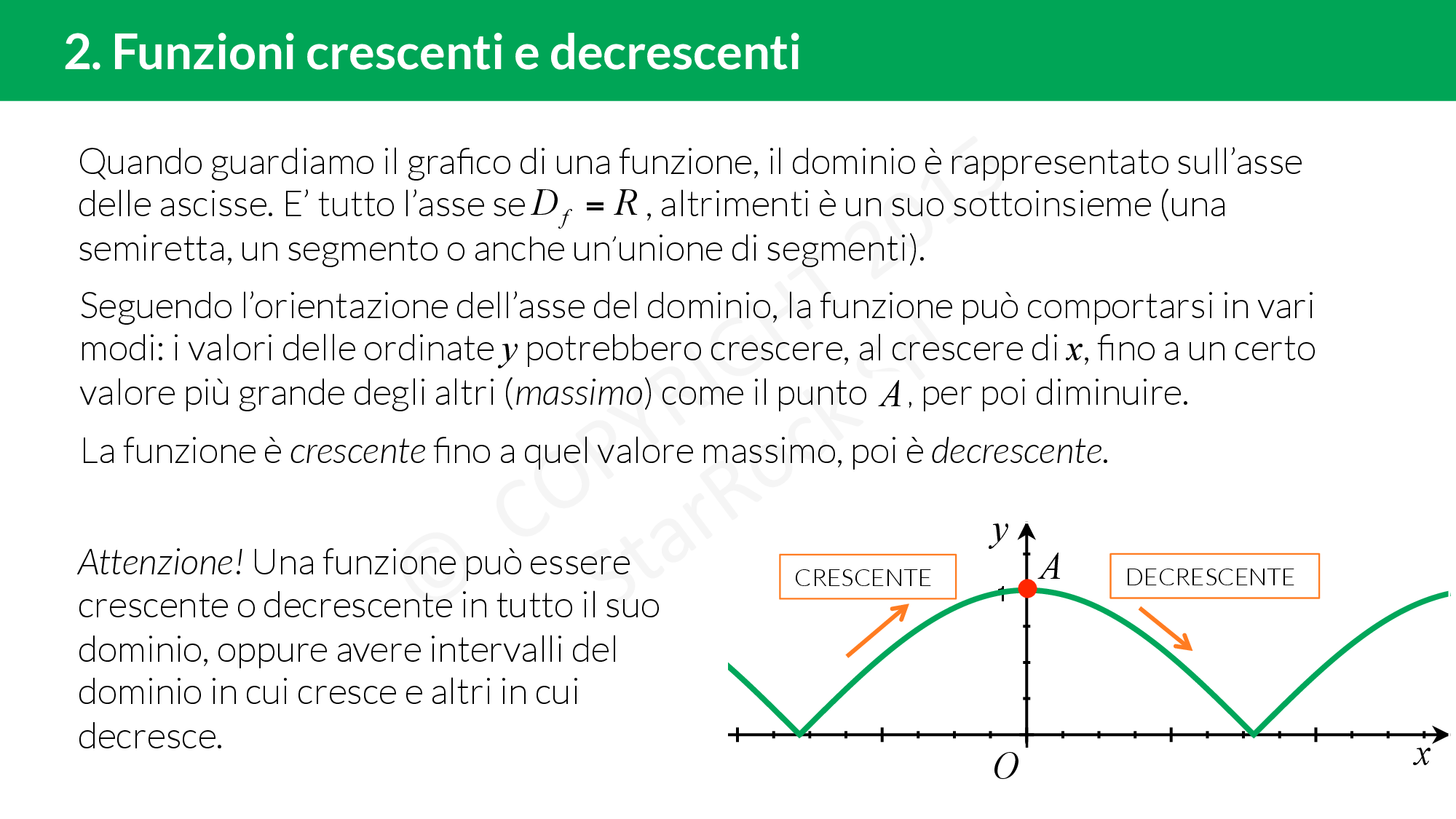
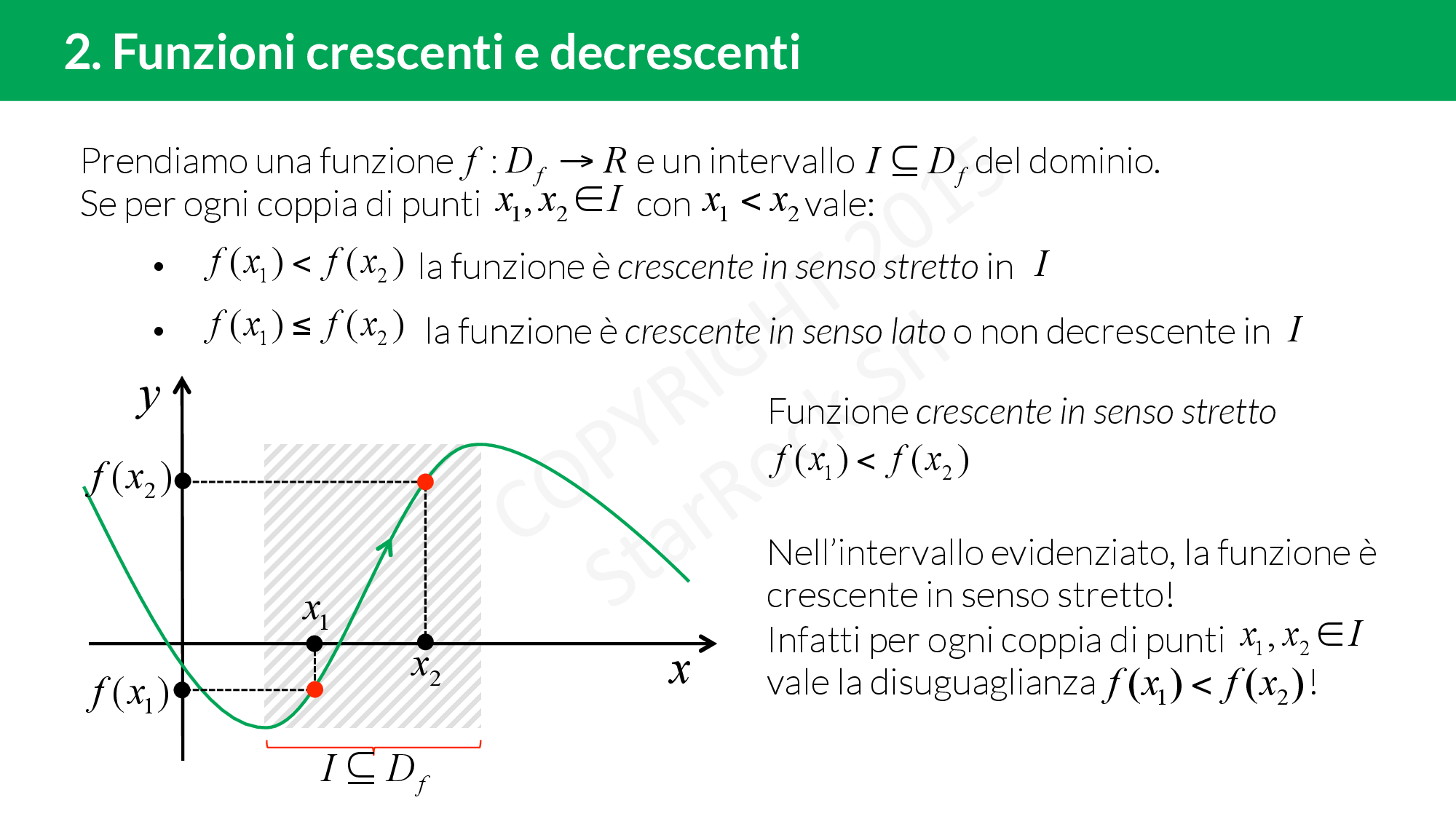
Monotonia: crescente o decrescente
Funzioni e proprietà: iniettive, suriettive, biunivoche, crescenti, decrescenti - Galleria
Una funzione è crescente se presi £$x_1 $£ e £$ x_2 $£ tali che £$x_1 \le x_2$£ allora £$ f(x_1) \le f(x_2) $£. Il grafico della funzione “va verso l’alto”.
Una funzione è decrescente se presi £$x_1 $£ e £$ x_2 $£ tali che £$x_1 \le x_2$£ allora £$ f(x_1) \ge f(x_2) $£. Il grafico della funzione “va verso il basso”.
Una funzione può essere crescente o decrescente in tutto il dominio, oppure crescente in un intervallo e decrescente in un altro.
Pari e dispari
Funzioni e proprietà: iniettive, suriettive, biunivoche, crescenti, decrescenti - Galleria
Una funzione è pari se i valori che assume per £$x 0 $£ vale a dire £$f(-x) = f(x)$£. Graficamente, una funzione pari ha il grafico simmetrico rispetto all’asse y.
Un esempio di funzione pari è £$y=x^2$£.
Una funzione è dispari se £$ f(x) = -f(-x)$£. In questo caso, il grafico della funzione è simmetrico rispetto all’origine degli assi.
Un esempio di funzione dispari è £$y=x^3$£.
A cosa serve sapere se una funzione è pari o dispari? Ci permette di studiare la funzione solo per £$x \ge 0 $£ perché per le [iol_placeholder type="formula" engine="katex" display="inline"]x
Ovviamente le funzioni possono anche non essere né pari né dispari.
Ripassa per l’interrogazione sulle funzioni
Funzioni e proprietà: iniettive, suriettive, biunivoche, crescenti, decrescenti - Galleria
Allenati con questi esercizi sulle proprietà delle funzioni per arrivare preparato alla prossima interrogazione o verifica!
Trovi tanti esercizi sulle proprietà delle funzioni: prova a superare i tre livelli di esercizi!
Sfida sulle proprietà delle funzioni
Testo e soluzione della sfida:
Funzioni e proprietà: iniettive, suriettive, biunivoche, crescenti, decrescenti - Galleria
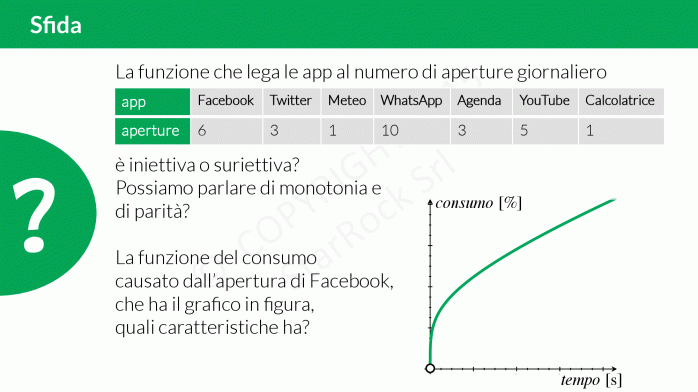
Quali sono le proprietà della funzione che associa a ogni app del tuo smartphone il numero di aperture giornaliere? È iniettiva? Magari è suriettiva?
Scoprilo risolvendo la sfida sulle proprietà delle funzioni!