Definizione di circonferenza e cerchio

La circonferenza e il cerchio sono degli oggetti molto diversi tra loro. Quante volte prima di iniziare un gioco ci è stato detto di metterci in cerchio? E se invece dovessimo metterci "in circonferenza"? Scopri tutto quello che devi sapere sugli elementi della circonferenza e del cerchio: impara a distinguere il raggio dal diametro, l'arco dalla corda, il segmento circolare dal settore circolare.

Appunti

La circonferenza e il cerchio… Sono la stessa cosa? No! Sono molto diversi tra loro!

Prova a pensare a quali oggetti della vita di tutti i giorni hanno la forma di una circonferenza: per esempio l’hula hoop oppure la ruota di una bicicletta! Una circonferenza è l’insieme dei punti equidistanti da un punto fisso chiamato centro. Se utilizziamo il compasso, la circonferenza è la linea tracciata dalla matita, il centro è il buchino lasciato dalla punta del compasso.

Un cerchio invece è l’area all’interno della circonferenza, cioè tutta la parte di piano delimitata da una circonferenza. Quindi quali oggetti hanno la forma di un cerchio? Pensa alle monete, oppure i vecchi dischi in vinile o ancora un semplice piatto… Per non parlare dei cerchi nel grano! ;)

Riconosci gli elementi della circonferenza e del cerchio e scopri qualche trucco per disegnare un cerchio anche senza il compasso!

Contenuti di questa lezione su: Definizione di circonferenza e cerchio

Definizione di cerchio e circonferenza

Le parti della circonferenza: corda, diametro, arco

Le parti del cerchio: segmento, settore e corona circolare

Come disegnare un cerchio?

Lezioni correlate

Accedi per sempre a tutte le lezioni FREE con video ed esercizi spiegati!

Registrati gratis

Definizione di cerchio e circonferenza

definizione circonferenza cerchio

Intorno a noi ci sono moltissimi oggetti rotondi. Sono cerchi! Sono circonferenze! Ma queste due parole vogliono dire la stessa cosa? In geometria, circonferenza e cerchio hanno significati diversi.

La circonferenza è l’insieme dei punti che sono tutti ad una stessa distanza da un punto fisso chiamato centro. Ogni segmento che unisce il centro ad un punto della circonferenza si chiama raggio.

Il cerchio, invece, è l’insieme dei punti che stanno all'interno di una circonferenza (se vogliamo dirlo in modo più matematico: il cerchio è la parte di piano delimitata da una circonferenza).

Distingui tutti gli oggetti che ti circondano: quali sono cerchi? E quali circonferenze?

Fai una segnalazione

Le parti della circonferenza: corda, diametro, arco

Per la circonferenza non parliamo di lati, diagonali, angoli... come abbiamo fatto per tutti gli altri poligoni. Ma possiamo riconoscere degli elementi particolari.

Una corda è un segmento che unisce due punti della circonferenza. Possiamo tracciare infinite corde, di lunghezze diverse. Il diametro è una corda che passa per il centro della circonferenza ed è la corda massima, cioè la più lunga di tutte. La lunghezza del diametro è doppia di quella del raggio.

Un arco, invece, è una parte di circonferenza delimitata da due punti. Se scegliamo 2 punti su una circonferenza, troviamo sempre due archi. Se i due punti che scegliamo sono gli estremi di un diametro, abbiamo trovato due semicirconferenze.

Indichiamo un arco di estremi £$ A $£ e £$ B $£ con una linea curva sopra £$ \overgroup{AB} $£. Diciamo che la corda £$ AB $£ è sottesa all'arco £$ \overgroup{AB} $£.

Vediamo ancora alcune proprietà di corde e archi che possono essere utili:

se due corde sono congruenti, allora si trovano alla stessa distanza dal centro;
se due archi sottendono due corde congruenti, allora anche gli archi sono congruenti.

Fai una segnalazione

Le parti del cerchio: segmento, settore e corona circolare

Segmento circolare

Settore circolare

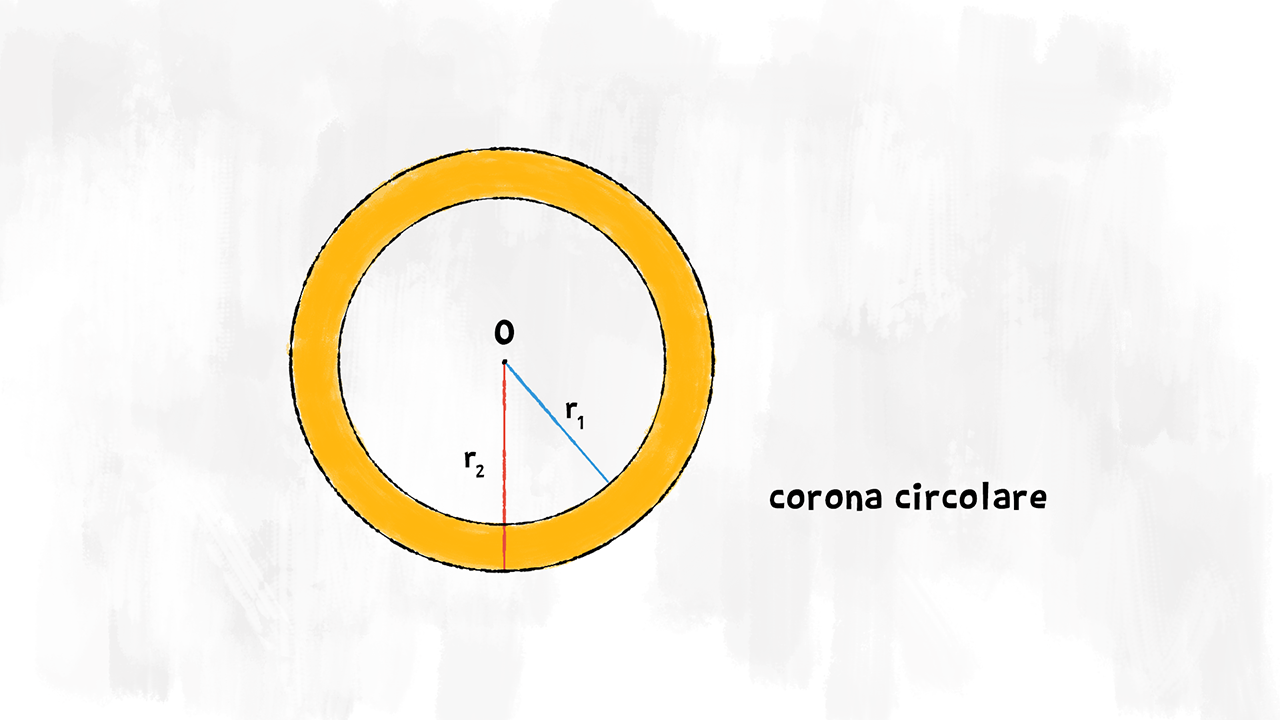
Corona circolare

Il cerchio come tutte le figure in geometria può essere suddiviso in parti. Ciascuna di queste parti ha un nome che lo definisce.

Se tracciamo una corda dividiamo il cerchio in due parti chiamate segmenti circolari. Se la corda che tracciamo è un diametro, i due segmenti circolari che troviamo sono uguali e sono dei semicerchi. Un segmento circolare è ciascuna delle due parti in cui un cerchio è diviso da una corda.

Come si chiama invece una fetta di cerchio? La parte di cerchio delimitata da due raggi e dall’arco di circonferenza compreso tra questi si chiama settore circolare. In una circonferenza di centro £$ O $£ disegniamo due raggi £$ OA $£ e £$ OB $£: indichiamo il settore circolare delimitato dall’arco £$ \overgroup{AB} $£ con i suoi tre vertici, come facciamo con i triangoli, ma utilizzando una linea curva, in questo modo £$ \overgroup{AOB} $£.

Due circonferenze con lo stesso centro, ma raggi di misura diversa, delimitano una corona circolare. Oggetti che ricordano una corono circolare sono il salvagente, oppure una ciambella.

Fai una segnalazione

Come disegnare un cerchio?

Quante volte ci troviamo in difficoltà nel disegnare un cerchio?

Che disastro arrivare a scuola e scoprire di aver dimenticato il compasso a casa, proprio nel giorno in cui la prof inizia un nuovo argomento: la circonferenza e il cerchio.

Pagine e pagine di esercizi con circonferenze, raggi, diametri, cerchi, ma non riusciamo a disegnare niente di meglio di un ovale. E tutti si chiedono: "come faceva Giotto a disegnare un cerchio perfetto?"

Non è impossibile disegnare un cerchio perfetto con quello che abbiamo a disposizione nel nostro astuccio o anche solo utilizzando le nostre mani!

Il modo più facile è ricorrere a degli oggetti rotondi che possiamo trovare nel nostro astuccio: un rotolino di nastro adesivo, oppure il temperino per un cerchio più piccolo. Non hai niente di tutto questo? Puoi provare a riprodurre un compasso con un semplice filo. Ad un’estremità leghi la matita e tieni ferma l’altra estremità con un dito regolando la lunghezza del raggio. Voilà! Altrimenti procurati una graffetta (di solito i professori ne hanno sempre una), punta una matita da una parte della graffetta e con la matita all'altra estremità… Ecco che riesci a disegnare un bel cerchietto! Non c’è neanche una graffetta?!? Allora bastano le tue mani! Per fare un cerchio più grosso, appoggia il polso sul foglio, tienlo ben saldo e fai girare il foglio… Ecco un cerchio quasi perfetto!

Prova a scoprire altri trucchi per diventare come Giotto!

Fai una segnalazione