Formulario di geometria solida: formule di superficie e volume
In questo articolo, ci concentreremo su uno dei capitoli fondamentali della geometria: la geometria solida. Nel particolare, costruiremo insieme un formulario completo che ci permetterà di calcolare in modo preciso l‘area e il volume dei solidi e dei solidi di rotazione.
Che cos’è un solido? In termini semplici, un solido è un oggetto tridimensionale. A differenza delle figure bidimensionali, come cerchi o quadrati, che hanno solo lunghezza e larghezza, un solido ha anche la profondità. Alcuni esempi comuni di solidi includono cubi, sfere, cilindri e coni.
E cosa intendiamo con “solidi di rotazione”? Un solido di rotazione è un oggetto tridimensionale che si ottiene ruotando una figura piana intorno a un asse. Ad esempio, se ruotiamo un rettangolo intorno a uno dei suoi lati, otteniamo un cilindro.
L’area di un solido, invece, è la misura della superficie che lo circonda, mentre il volume è la quantità di spazio che occupa. Sia l’area che il volume sono misure fondamentali in molte discipline, dalla matematica all’ingegneria, dalla fisica alla scienza dei materiali.
Questo formulario potrà tornarti utile ogni volta che dovrai ripassare o che non ricorderai una delle formule: puoi tornare qui ogni volta che ne avrai di bisogno! E alla fine dell’articolo, troverai anche una tabella completa con tutte le formule principali per calcolare l’area e il volume di tutti i solidi che studieremo oggi.
- Formula per calcolare la superficie del prisma
- Formula per calcolare il volume del prisma
- Formula per calcolare la superficie e il volume di un parallelepipedo
- Formula per calcolare la superficie e il volume di un cubo
- Formula per calcolare la superficie della piramide
- Formula per calcolare il volume della piramide
- Formula per calcolare la superficie del cilindro
- Formula per calcolare il volume del cilindro
- Formula per calcolare la superficie del cono
- Formula per calcolare il volume del cono
- Formule per calcolare la superficie e il volume della sfera
- Tabella con formule complete per calcolare superficie e volume dei solidi
Formula per calcolare la superficie del prisma

Chiamiamo £$A_b$£ l’area di base, £$S_l$£ la superficie laterale, £$S_{tot}$£ la superficie totale e £$h$£ l’altezza del prisma.
$$S_l = \text{perimetro di base} \cdot h $$ $$S_{tot} = A_b + A_b + S_l = 2A_b + S_l$$
Formule inverse:
$$ \text{perimetro di base} = \dfrac{S_l}{h} $$ $$ h =\dfrac{S_l}{\text{perimetro}}$$ $$ A_b = \dfrac{S_{tot}-S_l}{2}$$ $$ S_l = S_{tot}-2A_b$$
Formula per calcolare il volume del prisma
Chiamiamo £$A_b$£ l’area di base, £$ V $£ il volume del prisma e £$h$£ l’altezza del prisma.
$$V = A_b \cdot h$$
Formule inverse:
$$ A_b= \dfrac{V}{h}$$ $$ h =\dfrac{V}{A_b}$$
Formula per calcolare la superficie e il volume di un parallelepipedo
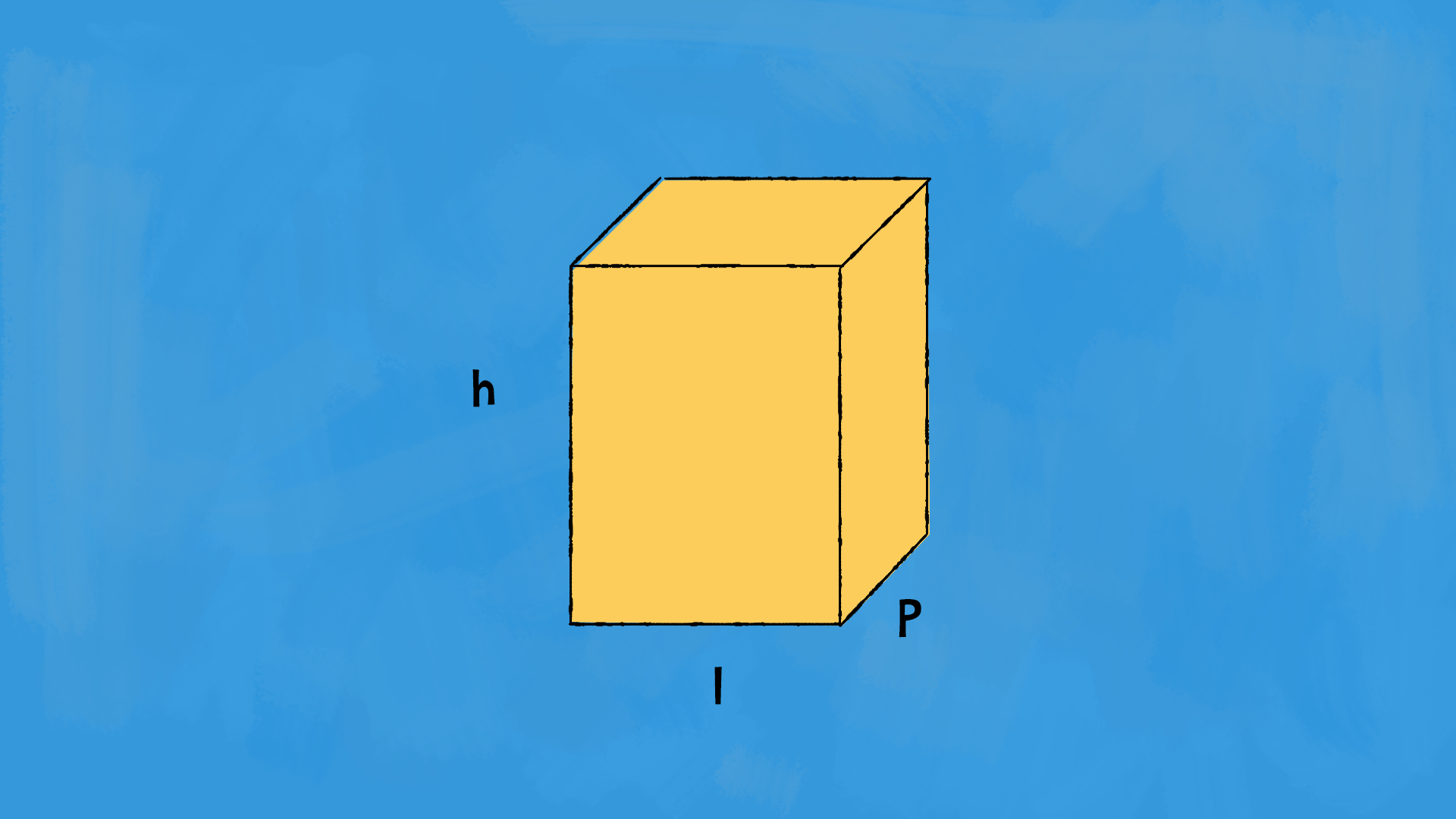
Il parallelepipedo è un solido che ha tutte le facce rettangolari. Conosciamo le misure del parallelepipedo: £$ l $£ è la larghezza, £$ p $£ è la profondità e £$ h $£ è l’altezza.
Chiamiamo £$ A_b $£ l’area di base. La superficie laterale di un parallelepipedo è:
$$ S_l = 2(l + p) \cdot h $$
La superficie totale di un parallelepipedo è:
$$ S_{tot} = S_l + 2 A_b $$
Il volume di un parallelepipedo è:
$$ V = l \cdot p \cdot h $$
Formula per calcolare la superficie e il volume di un cubo
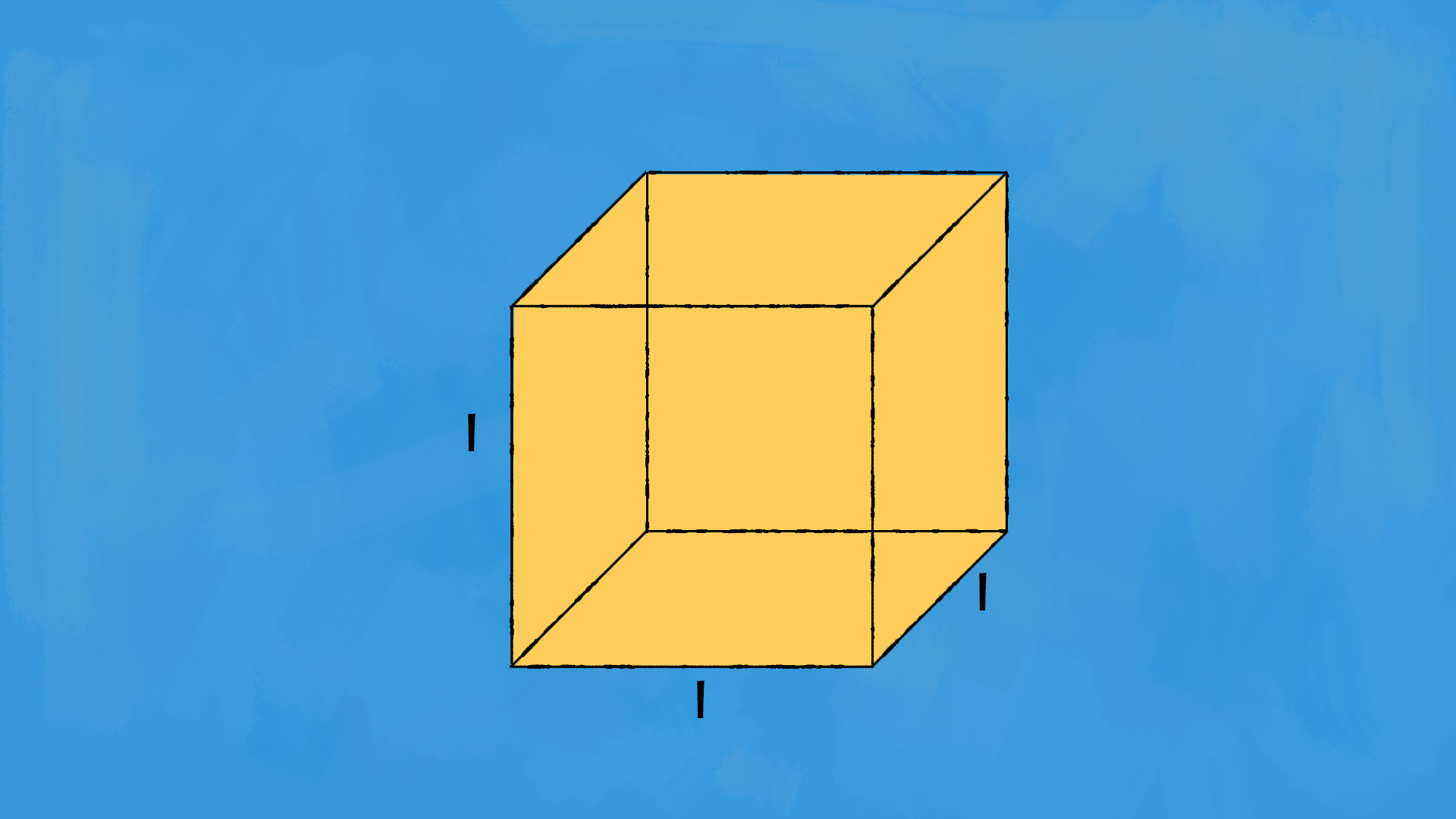
Il cubo è un solido formato da 6 facce quadrate di lato £$ \ell $£. Per calcolare la superficie totale di un cubo:
$$ S_{tot} = 6 \cdot \ell^2 $$
Il volume di un cubo invece è:
$$ V = \ell^3 $$
Formula per calcolare la superficie della piramide
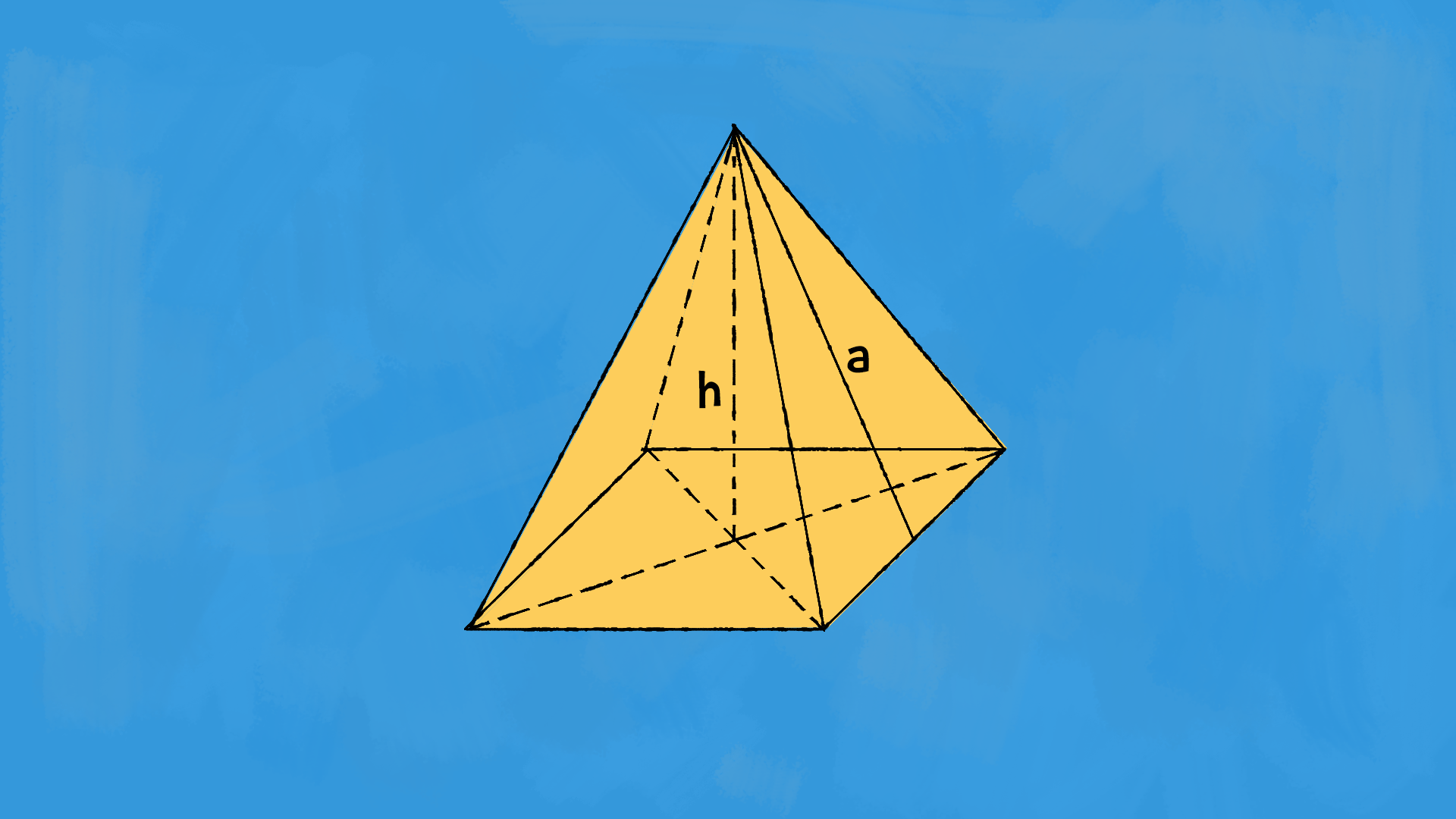
Chiamiamo £$A_b$£ l’area di base, £$S_l$£ la superficie laterale, £$S_{tot}$£ la superficie totale, £$a$£ apotema e £$h$£ l’altezza della piramide.
$$S_l =\dfrac{\text{perimetro di base} \cdot a} {2} $$ $$S_{tot} = A_b + S_l$$
Formule inverse:
$$\text{perimetro di base} =\dfrac{2S_l}{a}$$ $$ a = \dfrac{2S_l}{\text{perimetro}}$$ $$ S_l = S_{tot}-A_b$$ $$ A_b = S_{tot}-S_l$$
Formula per calcolare il volume della piramide
Chiamiamo £$A_b$£ l’area di base, £$V$£ il volume della piramide e £$h$£ l’altezza della piramide.
$$V = \dfrac{A_b \cdot h}{ 3}$$
Formule inverse:
$$ A_b=\dfrac{3V}{h}$$ $$ h=\dfrac{3V}{A_b}$$
Formula per calcolare la superficie del cilindro

Chiamiamo £$A_b$£ l’area di base, £$S_l$£ la superficie laterale, £$S_{tot} $£ la superficie totale, £$r$£ raggio del cilindro e £$h$£ l’altezza del cilindro.
$$ S_l = 2\pi \cdot r \cdot h$$ $$S_{tot} = 2A_b + S_l = 2\pi r^2 + 2\pi r h $$
Formule inverse:
$$ r= \dfrac{S_l}{2\pi\cdot h}$$ $$h =\dfrac{S_l}{2\pi\cdot r}$$ $$ A_b = \dfrac{S_{tot}-S_l}{2} $$ $$ S_l = S_{tot}-2A_b $$
Formula per calcolare il volume del cilindro
Chiamiamo £$A_b$£ l’area di base, £$V$£ il volume del cilindro e £$ h$£ l’altezza del cilindro.
$$V = A_b \cdot h = \pi r^2 \cdot h$$
Formule inverse:
$$ A_b =\dfrac{V}{h} $$ $$ h = \dfrac{V}{A_b} $$
Formula per calcolare la superficie del cono
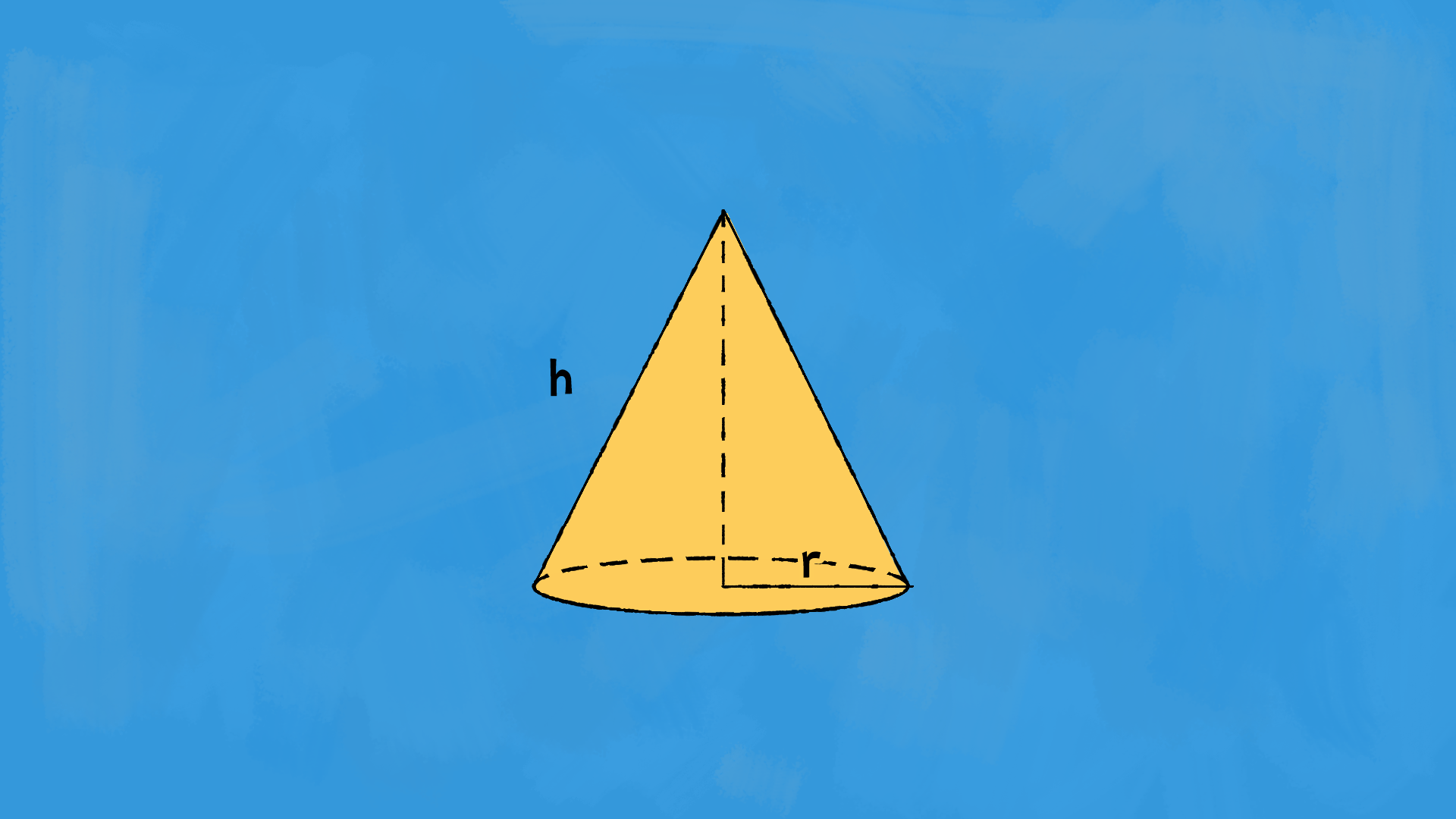
Chiamiamo £$A_b$£ l’area di base, £$S_l$£ la superficie laterale, £$S_{tot}$£ la superficie totale, £$r$£ raggio di base, £$a$£ apotema e £$h$£ l’altezza del cono.
$$S_l = \pi \cdot r \cdot a$$ $$S_{tot} = A_b + S_l = \pi r^2 + \pi r a $$
Formule inverse:
$$ r = \dfrac{S_l}{\pi\cdot a}$$ $$ a = \dfrac{S_l}{\pi\cdot r}$$ $$ S_l = S_{tot}-A_b $$ $$ A_b = S_{tot}-S_l $$
Formula per calcolare il volume del cono
Chiamiamo £$A_b$£ l’area di base, £$V$£ il volume del cono e £$h$£ l’altezza del cono.
$$V = \dfrac{A_b \cdot h}{3} =\dfrac {\pi r^2 h} {3}$$
Formule inverse:
$$ A_b = \dfrac{3V}{h} $$ $$ h = \dfrac{3V}{A_b} $$
Formule per calcolare la superficie e il volume della sfera

Chiamiamo £$S$£ la superficie, £$r$£ raggio della sfera, £$V$£ il volume.
$$S = 4 \cdot \pi r^2$$ $$V = \dfrac{4}{3} \cdot \pi \cdot r^3$$
Formule inverse:
$$ r= \sqrt{\dfrac{S}{4\pi}}$$ $$ r =\sqrt[3]{\dfrac{3V}{4\pi}}$$
Tabella con formule complete per calcolare superficie e volume dei solidi
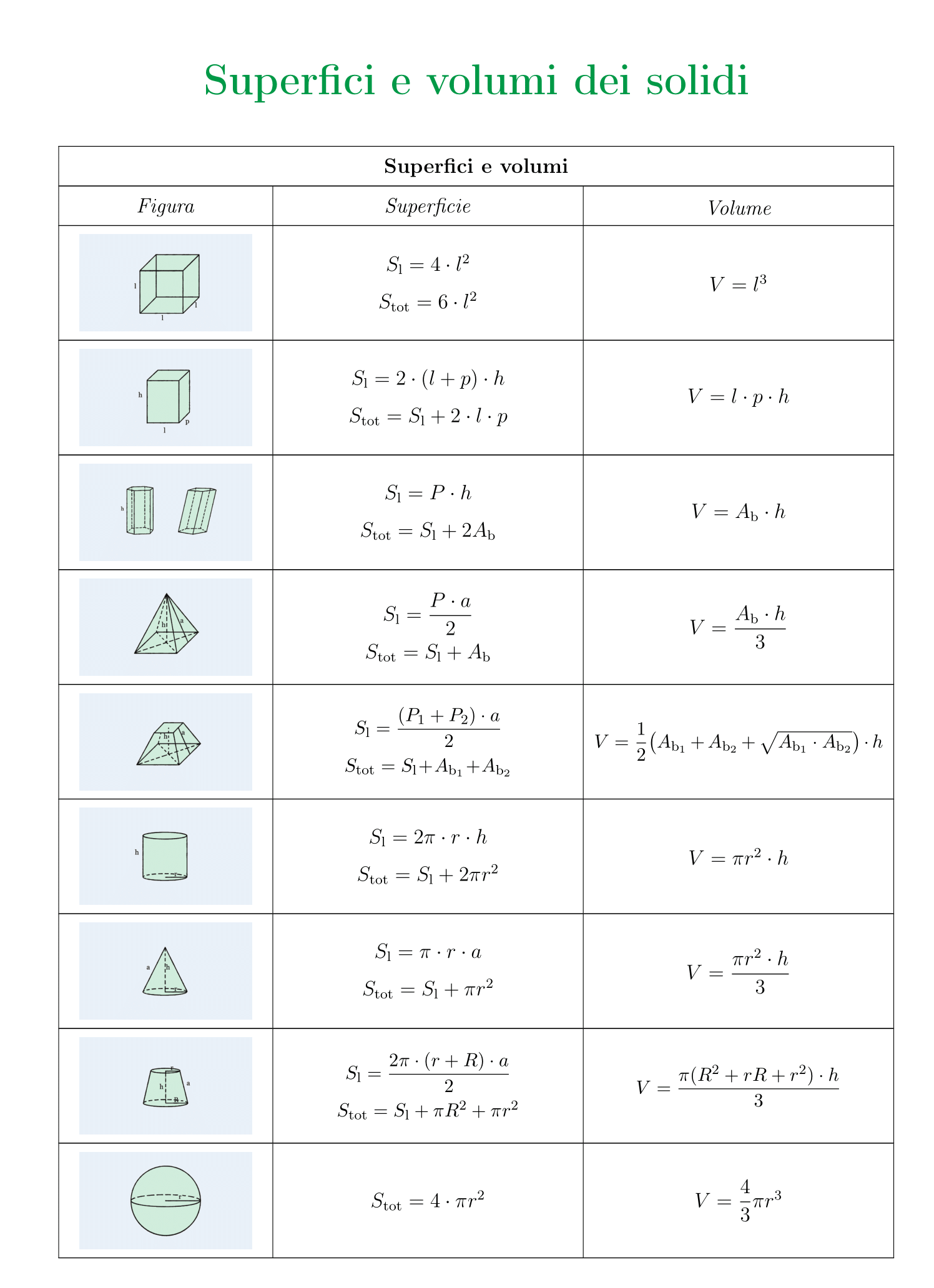
Per ricordare sempre come calcolare superficie e volume dei solidi e dei solidi di rotazione, potrebbe esserti utile avere una tabella riassuntiva che possa aiutarti ad avere sempre sotto mano tutte le formule, così da poterle utilizzare quando ne hai bisogno!
Relazione tra massa, densità e volume
Chiamiamo £$m$£ la massa, £$d$£ la densità e £$ V$£ il volume.
$$d =\dfrac {m}{V} \ (\text{kg/m}^3) $$
Formule inverse:
$$ m = d \cdot V \ (\text{kg}) $$ $$ V =\dfrac{m}{d} \ (\text{m}^3) $$
