Formulario di geometria: le formule sul piano cartesiano
Dalle piramidi dell’Antico Egitto alle opere d’arte rinascimentali e l’invenzione della prospettiva, la geometria ha sempre avuto un ruolo centrale nella comprensione e rappresentazione del mondo intorno a noi, ma è con l’avvento del piano cartesiano, introdotto dal filosofo e matematico René Descartes, conosciuto semplicemente come Cartesio, nel XVII secolo, che la geometria ha acquisito una nuova dimensione, fondendo insieme algebra e geometria in un unico sistema coerente.
Il piano cartesiano, con i suoi assi orizzontale e verticale e la sua griglia di coordinate, fornisce un modo per visualizzare equazioni algebriche come curve e forme geometriche. Questa fusione di numeri e figure ha aperto la porta a innumerevoli scoperte e applicazioni, dalle leggi del movimento di Newton alla teoria della relatività di Einstein. Ma prima di immergerci in queste applicazioni avanzate, è essenziale avere una solida comprensione delle formule di base che governano il piano cartesiano.
Scopriamole insieme!
- Le caratteristiche del piano cartesiano
- Le coordinate dei punti sul piano cartesiano
- Lunghezza di un segmento orizzontale: la formula per calcolarla
- Lunghezza di un segmento verticale: la formula
- Lunghezza di un segmento generico: la formula
Le caratteristiche del piano cartesiano
Il piano cartesiano è uno strumento fondamentale della matematica, una griglia bidimensionale su cui rappresentare punti, linee e curve attraverso coordinate numeriche. La sua genialità risiede nella sua semplicità e nella sua capacità di trasformare concetti algebrici in rappresentazioni visive. Ma, quali sono gli elementi che definiscono il piano cartesiano?
- Assi cartesiani: Il piano cartesiano è definito da due assi perpendicolari: l’asse orizzontale, noto come asse delle ascisse o asse x, e l’asse verticale, chiamato asse delle ordinate o asse y. L’intersezione di questi due assi è chiamata origine, ed è il punto (0,0).
- Quadranti: Gli assi cartesiani dividono il piano in quattro regioni, chiamate quadranti. Il primo quadrante si trova in alto a destra, dove entrambe le coordinate sono positive. Procedendo in senso orario, i quadranti sono numerati dal II al IV, con varie combinazioni di coordinate positive e negative.
- Coordinate: Ogni punto nel piano cartesiano è identificato da una coppia ordinata di numeri (x,y), dove x indica la posizione lungo l’asse delle ascisse e y lungo l’asse delle ordinate. Questo sistema di coordinate permette di localizzare esattamente ogni punto nel piano.
- Retta dei numeri: Oltre alla rappresentazione bidimensionale, ogni asse può essere visto anche come una retta dei numeri, con un’infinità di punti che rappresentano tutti i numeri reali, sia positivi che negativi, con l’origine che rappresenta lo zero.
- Distanza e pendenza: Nel contesto del piano cartesiano, è possibile calcolare la distanza tra due punti utilizzando il teorema di Pitagora. Inoltre, la pendenza di una retta può essere determinata considerando il rapporto tra la variazione delle ordinate e quella delle ascisse tra due punti sulla retta.
Le coordinate dei punti sul piano cartesiano
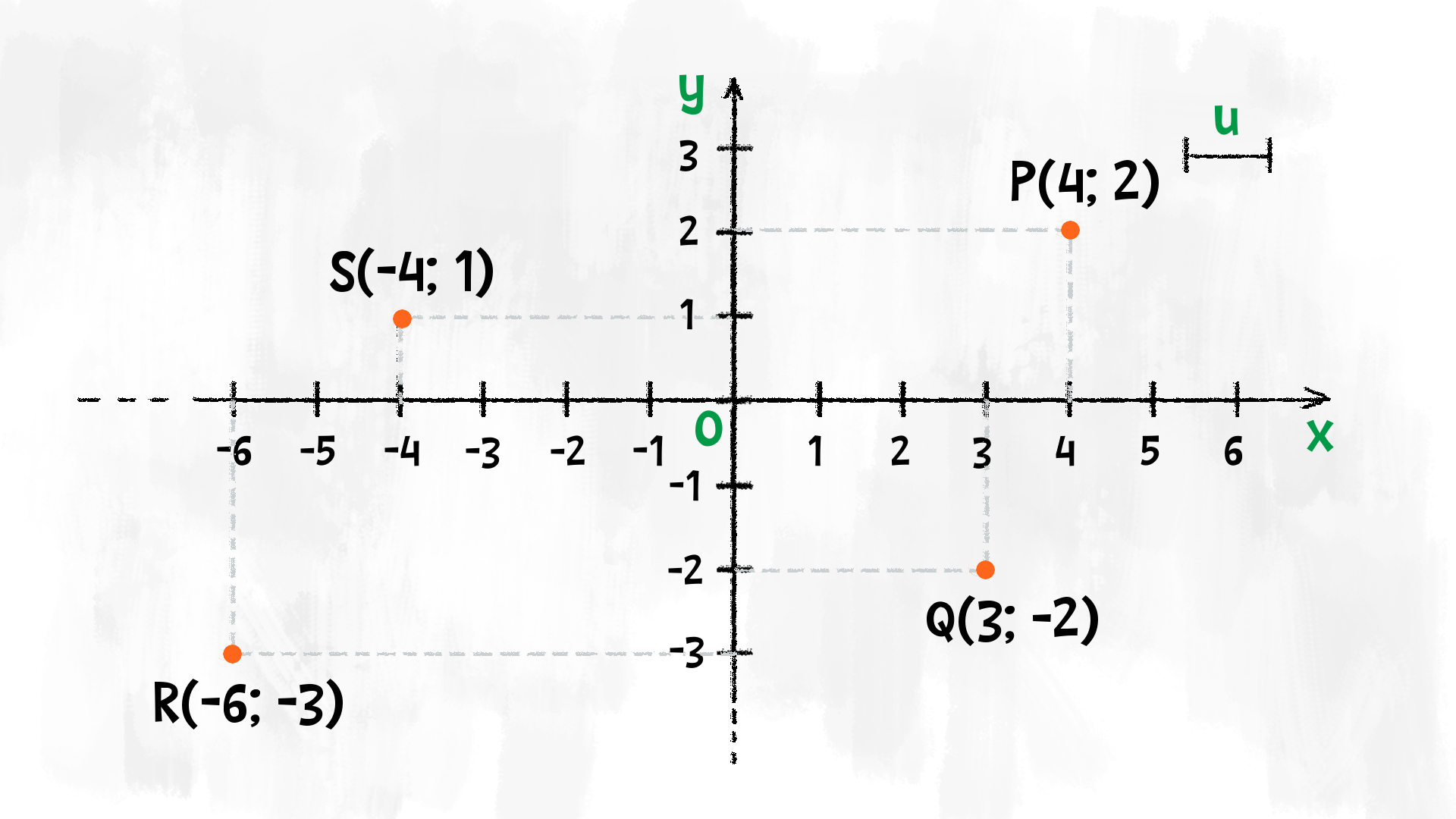
Il piano cartesiano è formato da due assi perpendicolari, detti ascissa (asse delle £$x$£) e ordinata (asse delle £$y$£). La posizione di un punto £$ P $£ sul piano è individuata da due numeri scritti tra parentesi, separati da un punto e virgola. Sono le coordinate del punto: il primo numero indica l’ascissa, mentre il secondo l’ordinata.
$$P(x; y)$$
Il primo numero, cioè £$x$£, indica la posizione lungo l’asse delle ascisse; il secondo numero, cioè £$y$£, indica la posizione lungo l’asse delle ordinate.
Lunghezza di un segmento orizzontale: la formula per calcolarla
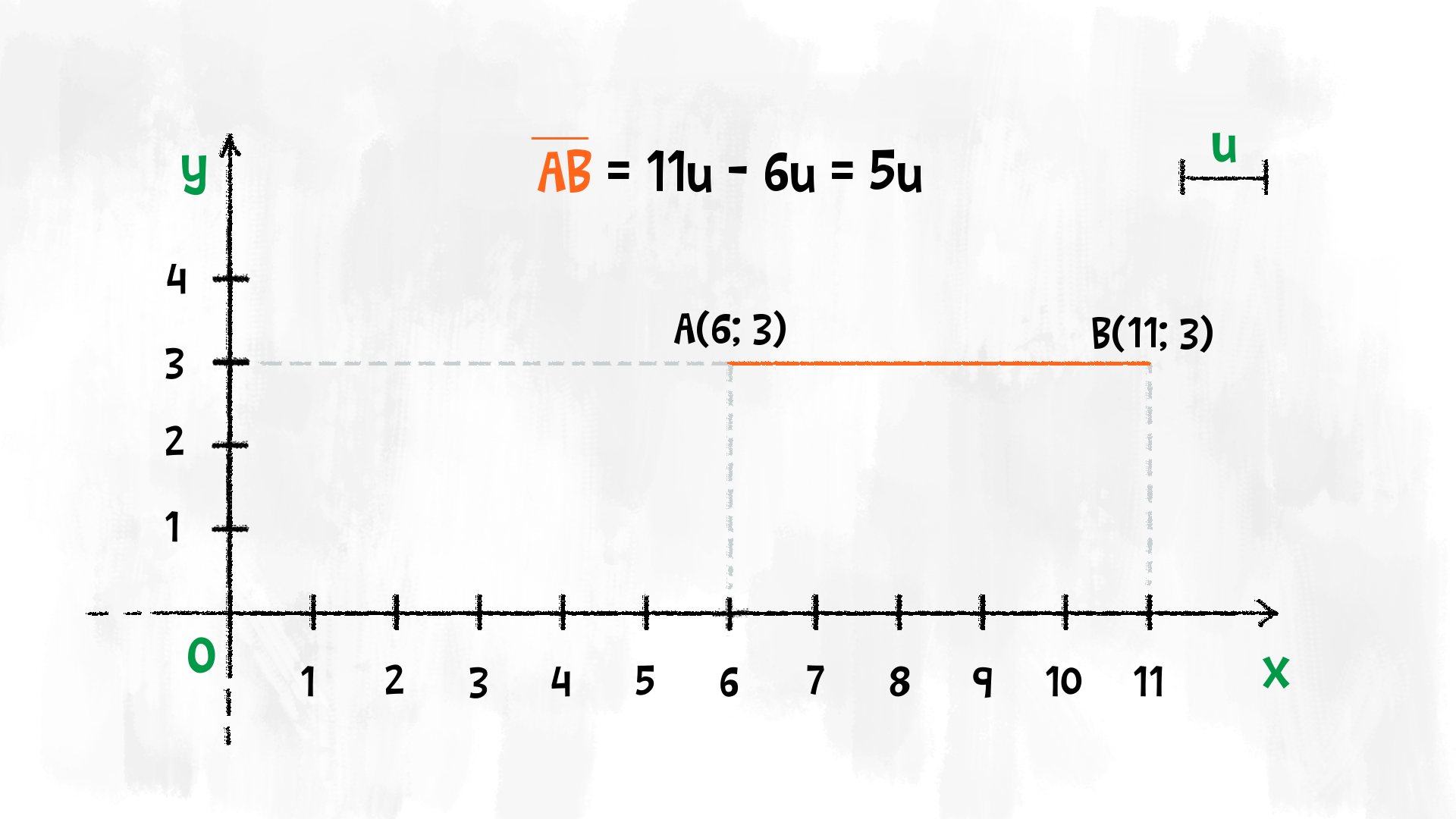
Possiamo calcolare la lunghezza di un segmento orizzontale £$\overline{AB}$£ con una semplice differenza tra le ascisse.
Se £$x_B > x_A$£, troviamo che il segmento ha lunghezza £$\overline{AB} = x_B − x_A$£, altrimenti viceversa.
Lunghezza di un segmento verticale: la formula

Possiamo calcolare la lunghezza di un segmento verticale £$\overline{AB}$£ con un semplice differenza tra le ordinate.
Se £$y_B > y_A$£, troviamo che il segmento ha lunghezza £$\overline{AB} = y_B – y_A$£, altrimenti viceversa.
Lunghezza di un segmento generico: la formula
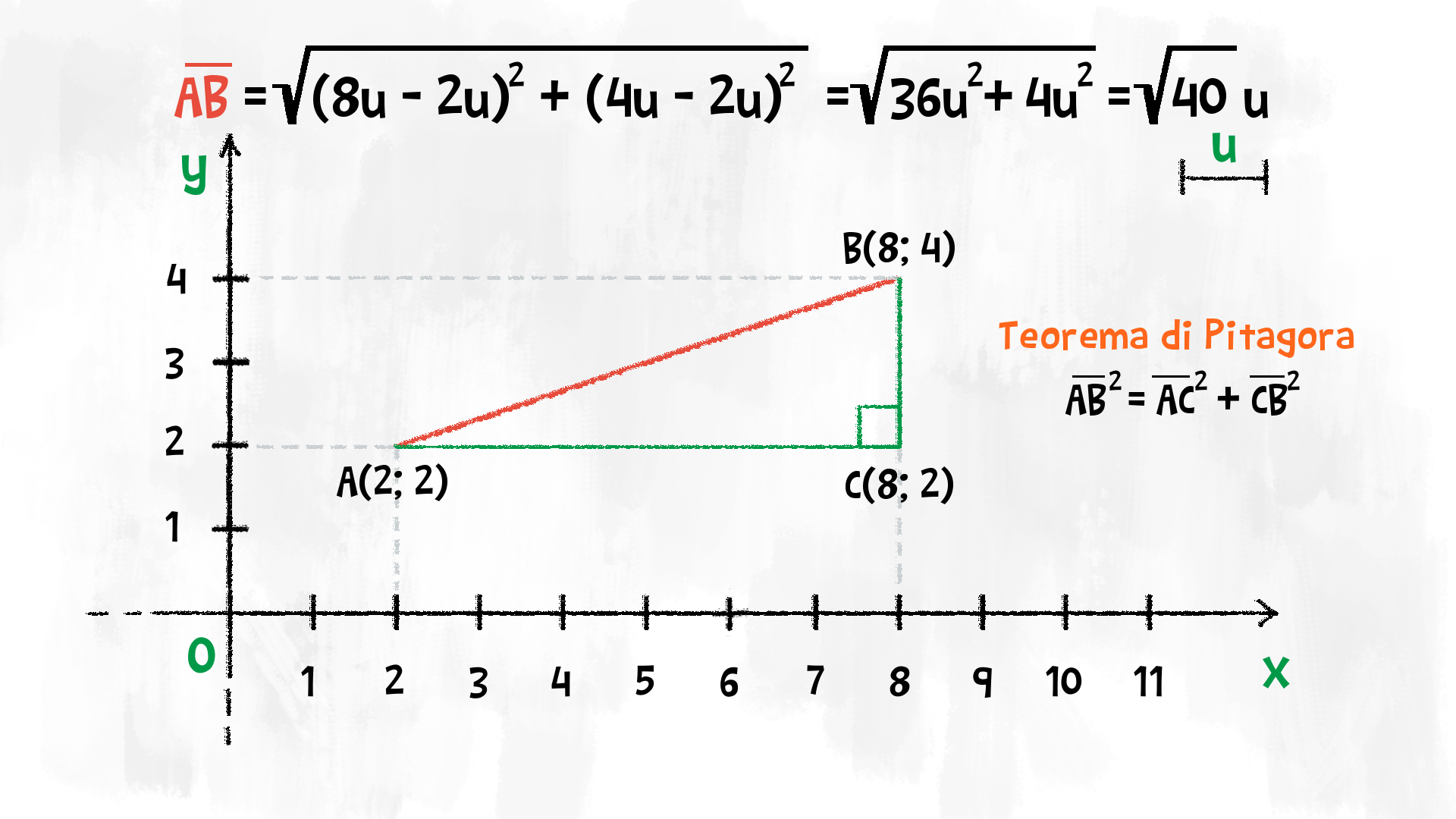
Possiamo calcolare la lunghezza di un segmento generico £$\overline{AB}$£ utilizzando il teorema di Pitagora.
£$(x_B − x_A)$£ e £$(y_B − y_A)$£ sono i cateti, mentre il segmento £$\overline{AB}$£ è l’ipotenusa del triangolo rettangolo che costruiamo sul piano cartesiano.
$$\overline{AB}=\sqrt{(x_B−x_A)^2+(y_B−y_A)^2}$$
