Coni: come calcolare superficie e volume
In questo articolo ci focalizzeremo su una forma tridimensionale che molto familiare per tanti: il cono. Un cono, nella sua accezione geometrica, è una figura solida che si forma quando si tracciano linee rette (dette generatrici) che congiungono tutti i punti di una figura piana (la base) con un punto fuori da essa (il vertice). Ma come possiamo descrivere matematicamente un cono? Quali sono le formule per calcolare la superficie e il volume di un cono? E come possiamo applicare queste formule nella pratica?
Queste sono alcune delle domande alle quali cercheremo di rispondere in questo articolo. Attraverso spiegazioni semplici e passaggi chiari, faremo luce su questi concetti fondamentali della geometria, offrendo una comprensione più approfondita di cosa siano i coni e come si possano calcolare la loro superficie e il volume.
Può sembrare complesso farlo a causa della necessità di calcolare l’apotema del cono, ma con la giusta pratica sarà molto più semplice di quanto pensi!
- Che cos'è il cono
- Quali sono le sezioni del cono
- Come calcolare la superficie del cono
- Come calcolare il volume del cono
Che cos’è il cono
Per generare un cono circolare retto occorre far ruotare un triangolo rettangolo di un giro completo attorno a uno dei suoi cateti: questo è il cateto che rimane fisso nella rotazione.
Se posiamo un cono su un tavolo in modo che non rotoli via lo abbiamo sicuramente appoggiato sulla sua base. I coni hanno una base e una punta, il vertice, proprio come le piramidi.
La base del cono è un cerchio.
L’asse di rotazione è quella retta a cui appartiene il cateto del triangolo che rimane fisso durante la rotazione: si chiama anche asse del cono.
L’asse passa per il vertice e per il centro della base ed è perpendicolare ad essa.
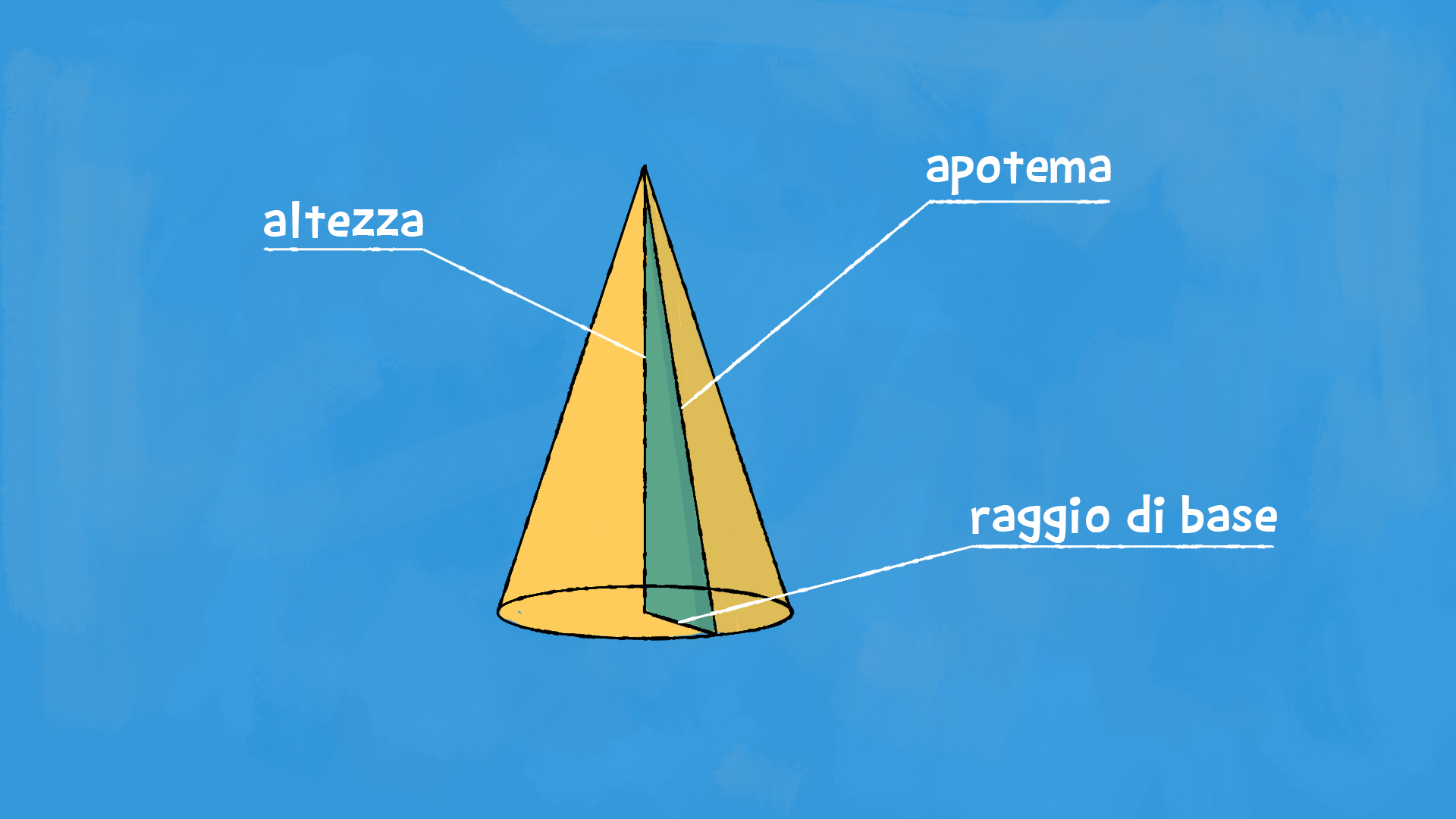
Il raggio del cono è il raggio della base. È congruente all’altro cateto del triangolo, quello che non rimane fisso, cioè quello che non forma l’asse del cono (o l’asse di rotazione).
La distanza tra la base e il vertice si chiama altezza del cono. L’altezza è congruente al cateto del triangolo che rimane fisso. L’altezza è perpendicolare alla base.
L’apotema del cono è congruente all’ipotenusa del triangolo che lo genera.
Quali sono le sezioni del cono
Se affettiamo un cono con dei piani paralleli alla base otteniamo tutte sezioni circolari.
Mentre ci avviciniamo al vertice, le sezioni diventano sempre più piccole.
Se affettiamo un cono con un piano che contiene l’asse di rotazione otteniamo una
sezione triangolare! Questa sezione è un triangolo isoscele di area doppia rispetto a quello che ha generato il cono.
La base del triangolo è il diametro di base del cono.
L’altezza del triangolo è l’altezza del cono.
Il lato obliquo è l’apotema del cono.
Se la sezione è un triangolo equilatero, il cono si chiama equilatero. In un cono equilatero l’apotema è uguale al diametro della base.
Come calcolare la superficie del cono
Se apriamo una scatola a forma di cono otteniamo il suo sviluppo. Lo sviluppo del cono è simile allo sviluppo delle piramidi. È composto da:
- un cerchio;
- un settore circolare.
Il cerchio è la base del cono e sai già come calcolare la sua area. L’area di base del cono è $$ A_b=\pi r^2 $$ $$ r=\sqrt{\dfrac{A_b}{\pi}} $$
Il settore circolare corrisponde alla superficie laterale del cono: ha come raggio l’apotema del cono; l’arco che lo delimita è congruente alla circonferenza della base. La superficie laterale del cono è £$ \dfrac{2\pi \cdot\text{raggio}\cdot \text{apotema}}2=\pi\cdot\text{raggio}\cdot\text{apotema}$£. $$ S_l=\pi r a $$ $$ r=\dfrac{S_l}{\pi a} $$ $$ a=\dfrac{S_l}{\pi r} $$
La superficie totale del cono, come quella delle piramidi, è uguale alla somma della superficie di base e della superficie laterale. $$S_\text{tot}=A_b+S_l=\pi r^2+\pi r a$$
Come calcolare il volume del cono
Piramidi e coni hanno molto in comune: sono tutti solidi con una base e una punta.
Il volume del cono, come quello delle piramidi, si ottiene moltiplicando l’area di base per l’altezza e dividendo tutto per £$ 3 $£. $$V=\dfrac{A_b\cdot h}3=\dfrac{\pi r^2 h}3$$ $$ S_b=\dfrac{3V}{h} $$ $$ r=\sqrt{\dfrac{3V}{\pi h}} $$ $$ h=\dfrac{3V}{A_b}=\dfrac{3V}{\pi r^2} $$
