La piramide: cos'è e come si calcolano la superficie e il volume
La piramide in geometria è molto simile a quella egizia che tutti conosciamo: la definizione geometrica, però, è quella di un poliedro che ha come basi da una parte un qualsiasi poligono e dall’altra un vertice; le facce della piramide, invece, sono tutte dei triangoli.
Questa definizione è molto generica ed esistono tante diverse tipologie di piramide che vedremo all’interno di questa lezione.
- Cos'è una piramide in geometria
- Le piramidi e le sezioni di piramidi
- Come trovare l'apotema di una piramide
- Come calcolare la superficie laterale e totale di una piramide
- Come calcolare il volume di una piramide
Cos’è una piramide in geometria

Che cosa sono le piramidi? Sono solidi che hanno la stessa forma delle tombe che hanno costruito gli antichi egizi!
Una piramide è un poliedro in cui riconosciamo una base (che può essere un poligono qualsiasi) e un punto che non appartiene alla base, chiamato vertice. Le facce laterali della piramide sono triangoli ottenuti collegando i vertici del poligono di base al vertice della piramide. Una piramide è un solido a punta.
La base della piramide è un poligono. L’altezza di una piramide è il segmento che parte dal vertice e cade perpendicolarmente sulla base della piramide.
Una piramide è retta se il poligono di base può essere circoscritto ad una circonferenza e l’altezza della piramide cade nel centro di quella circonferenza. Una piramide è regolare se la base è un poligono regolare. Esistono anche delle piramidi che non sono né rette né regolari.
Tutte le piramidi che non sono rette, invece, possono essere definite come piramidi oblique.
Le piramidi possono essere distinte anche a seconda della base che hanno:
- una piramide che ha come base un quadrilatero è definita piramide quadrangolare;
- una piramide che ha come base un triangolo è definita piramide triangolare;
- una piramide che ha come base un quadrato è definita piramide a base quadrata.
E così via.
Le piramidi e le sezioni di piramidi
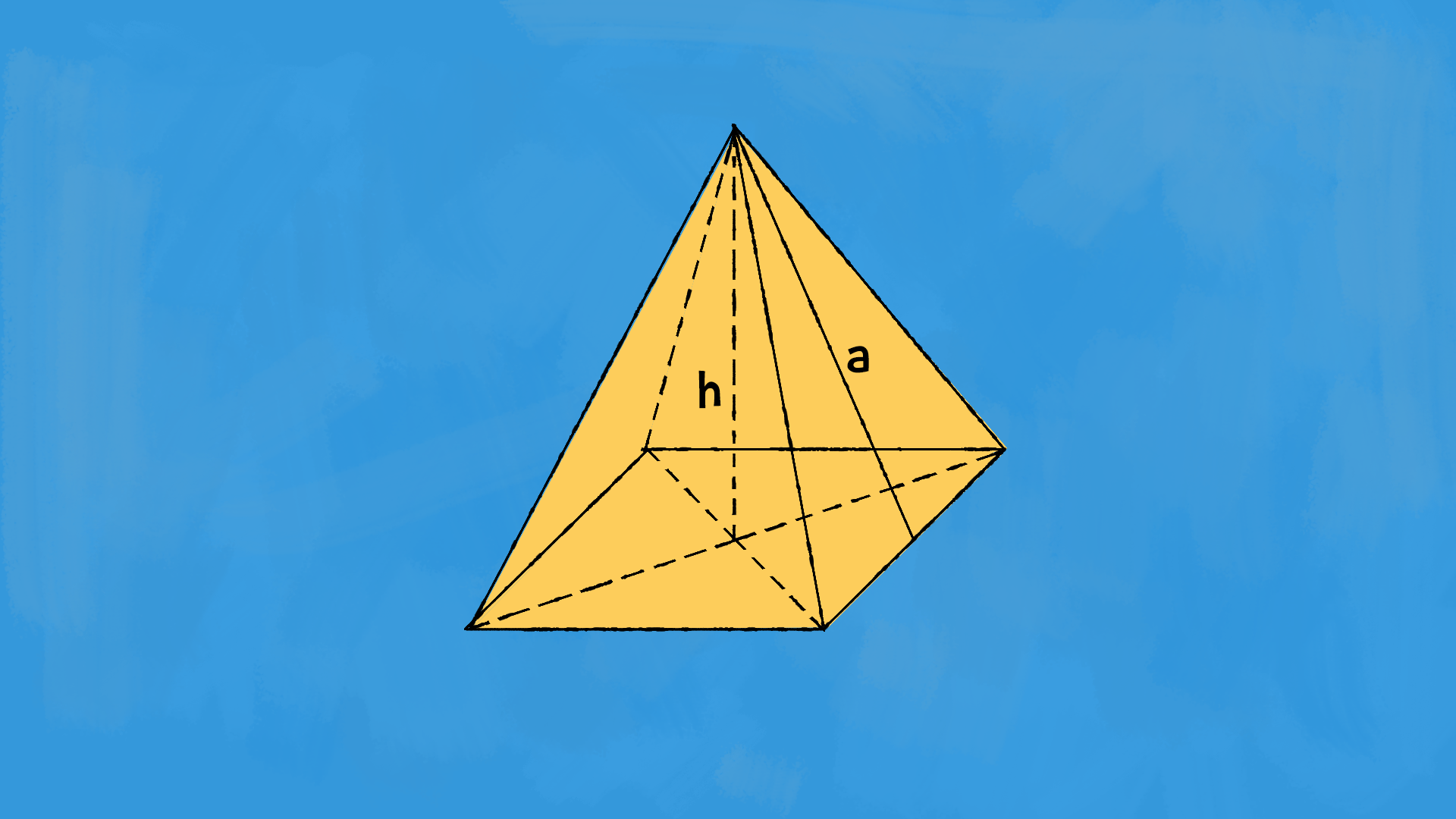
Le piramidi sono solidi a punta. Riconosciamo una base e un vertice a cui sono collegati tutti i vertici del poligono di base. Una piramide è retta se il poligono di base è circoscrivibile a una circonferenza e l’altezza cade esattamente al centro di questa circonferenza. Se il poligono di base non può essere circoscritto ad una circonferenza (è il caso per esempio del rettangolo) oppure se l’altezza cade al di fuori della base della piramide, non è una piramide retta. Noi ci occuperemo principalmente delle piramidi rette.
L’altezza di una piramide corrisponde alla distanza tra il vertice e la base. L’apotema di una piramide retta è l’altezza di una delle facce laterali, cioè l’altezza di ciascuno dei triangoli che formano la superficie laterale della piramide.
L’area di base di una piramide è la superficie del poligono di base. La superficie laterale è la somma delle aree di ciascuno dei triangoli che formano le pareti laterali. E il volume, sai cos’è? Immagina di riempire una piramide di acqua: quanta ce ne può stare?
Cosa succede invece se affettiamo una piramide? Se la tagliamo con piani paralleli alla base, la sezione è simile alla base della piramide: man mano che ci allontaniamo dalla base avvicinandoci al vertice, la sezione si rimpicciolisce. Se invece la tagliamo con piani perpendicolari alla base, otteniamo figure diverse.
Scopriamo insieme tecniche e formule per calcolare la superficie e il volume di una piramide.
Come trovare l’apotema di una piramide
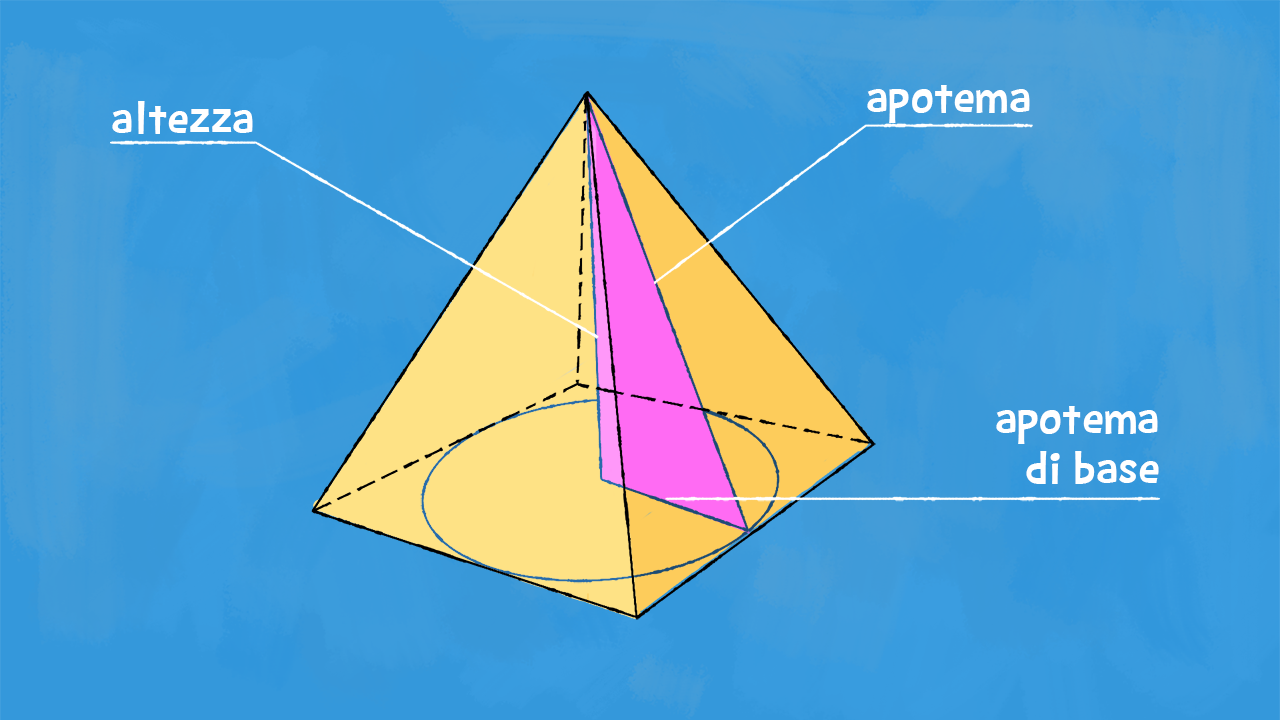
Abbiamo capito che l’altezza di una piramide corrisponde alla distanza tra il vertice e la base. Che cos’è invece questo apotema? E come facciamo a trovarlo?
In una piramide retta il poligono di base è circoscrivibile ad una circonferenza, quindi troviamo un apotema anche nella base: è il raggio della circonferenza inscritta nella base! Questo si chiama apotema di base: lo chiamiamo £$ r $£ e lo calcoliamo così £$ r = \dfrac{2\cdot \text{Area}}{\text{perimetro}} $£.
Troviamo poi un altro apotema: l’altezza di ciascuna delle facce laterali. Le facce che formano la superficie laterale di una piramide sono tutte triangolari, quindi ci serve conoscere la misura della loro altezza per poter calcolare la superficie del solido. Prendiamo la sezione della piramide che contiene il vertice e uno dei punti di tangenza tra il poligono di base e la circonferenza inscritta nel poligono. Otteniamo un triangolo! Ci basta considerarne metà: è un triangolo rettangolo in cui uno dei due cateti è congruente all’altezza della piramide, l’altro è congruente all’apotema di base. Grazie al teorema di Pitagora, possiamo trovare il terzo lato del triangolo: questo è l’apotema della piramide! Infatti, se consideriamo una faccia laterale della piramide, vediamo che questo segmento parte dal vertice e arriva perpendicolarmente sulla base: è proprio l’altezza della faccia laterale che stiamo considerando!
Se la piramide è regolare e retta, tutti i triangoli che formano la superficie laterale sono congruenti: sono triangoli isosceli! Se la piramide è solo retta, invece, le facce laterali sono triangoli tutti con la stessa altezza, ma potrebbero non essere congruenti.
Come calcolare la superficie laterale e totale di una piramide
Prendiamo una piramide retta e proviamo ad aprirla. Quello che troviamo è il suo sviluppo piano, cioè l’insieme di tutte le sue facce: una è la base, cioè un poligono qualsiasi (circoscrivibile ad una circonferenza), le altre sono tanti triangoli quanti sono i lati del poligono di base, e formano le pareti laterali. Chiamiamo £$ A_b $£ l’area di base, £$ S_l $£ la superficie laterale e £$ S_{tot} $£ la superficie totale.
L’area di base di una piramide dipende dal tipo di piramide che abbiamo di fronte: ripassa le aree dei poligoni!
La superficie laterale di una piramide è la somma delle aree di tutti i triangoli che formano le sue pareti. Qual è l’area di ciascuno di questi triangoli? È uguale alla metà del prodotto tra un lato del poligono e l’altezza di ciascuno di questi triangoli che formano la superficie laterale. Nel caso di una piramide retta, quindi, la superficie laterale è uguale al prodotto del perimetro del poligono di base per l’apotema della piramide, tutto diviso £$ 2 $£. Possiamo vedere la superficie laterale di una piramide retta come la metà di un parallelogramma che ha per base il perimetro del poligono di base e per altezza l’apotema.
$$ S_l = \dfrac{\text{perimetro di base} \cdot \text{apotema della piramide}}{2} $$
Esempio: una piramide esagonale regolare retta con lato di base £$ \ell $£ e apotema £$ a $£ ha per superficie laterale £$ S_l = \dfrac{6 \cdot \ell \cdot a}{2} $£.
E come si trova la superficie totale? Basta sommare superficie laterale e area di base.
$$ S_{tot} = A_b + S_l $$
Esempio: la superficie totale della nostra piramide esagonale regolare retta con lato di base £$ \ell $£ e apotema £$ a $£ è £$ S_{tot} = A_b + S_l $£.
Come facciamo a calcolare la superficie laterale di una piramide qualsiasi? Possiamo fare la stessa cosa, però dobbiamo fare attenzione: i triangoli che formano le facce laterali possono non essere tutti congruenti. In questo caso dobbiamo trovare l’altezza di ciascuna faccia laterale e poi sommare tutte le aree. Fai sempre attenzione e ricordati che l’unità di misura per le superfici è il £$ \text{m}^2 $£!
Come calcolare il volume di una piramide
Le piramidi egizie dovevano essere molto spaziose, per contenere la tomba del faraone, tutti i suoi oggetti, tutto quello che poteva essere utile nell’aldilà, ma anche le trappole per tenere lontano visitatori indesiderati. A seconda dell’importanza del faraone, la piramide è più o meno capiente. Anche gli egizi avevano bisogno di calcolare il volume!
Il volume di una piramide indica lo spazio che occupa il solido. Inoltre il volume indica anche qual è la capacità di quel solido, cioè quanto può contenere. Il volume di una piramide qualsiasi di altezza £$ h $£ è uguale a un terzo del prodotto tra l’area di base della piramide e l’altezza.
$$ V = \dfrac{A_b \cdot h}{3} $$
Ricorda che stiamo calcolando un volume! L’unità di misura del volume è £$ \text{m}^3 $£.
