Il prisma: come si calcola la superficie e il volume

Tra i vari poliedri esistenti, una tra le categorie più famose è quella del prisma. In particolare, un prisma può essere definito come un poliedro formato da due poligoni paralleli e uguali, che rappresentano le sue basi, ed ha come facce laterali dei parallelogrammi. Il numero totale di parallelogrammi dipenderà dal numero di lati dei poligoni alla base.

In particolare, una sotto-categoria dei prismi sono i parallelepipedi, perché si tratta di un vero e proprio prisma che ha dei parallelogrammi non soltanto come facce laterali, ma anche come basi.

Anche il cubo è una particolare categoria di prisma: si tratta di un prisma le cui facce sono tutte uguali, cioè dei quadrati.

In questo articolo potrai imparare cosa sono i prismi, come se ne calcola la superficie e il volume e quali sono le sotto-categorie più importanti di prisma, cioè il cubo e il parallelepipedo. Scopriamole insieme!

• Cos'è un prisma
• Il prisma e le sezioni dei prismi
• Come si calcola la superficie laterale e totale di un prisma
• Come si calcola il volume di un prisma
• Un prisma particolare: il parallelepipedo
• Il prisma con le facce quadrate: il cubo

Cos’è un prisma

Il prisma sono poliedri particolari: due delle loro facce si chiamano basi e sono poligoni congruenti e paralleli tra loro, cioè figure che appartengono a due piani paralleli. Infatti i prismi sono solidi a due basi!

I poligoni che formano le basi danno il nome al prisma:

• se la base è un triangolo, lo chiamiamo prisma triangolare;
• se la base è un quadrato, lo chiamiamo prisma quadrangolare;
• se la base è un pentagono, lo chiamiamo prisma pentagonale;
• se la base è un esagono, lo chiamiamo prisma esagonale;
• …e così via.

Possiamo parlare di prisma retto e prisma obliquo: un prisma è retto se le sue facce laterali sono dei rettangoli, è obliquo se le facce laterali sono dei parallelogrammi generici (non rettangoli).

Esistono poi dei prismi particolari: i parallelepipedi. Un prisma è un parallelepipedo quando tutte le facce sono dei rettangoli. E se tutte le facce sono dei quadrati, ritroviamo il cubo!

Un prisma regolare è un prisma che ha per base un poligono regolare: triangolo equilatero, quadrato, pentagono regolare, esagono regolare.

Il prisma e le sezioni dei prismi

I prismi sono solidi a due basi. Le due basi sono poligoni congruenti disposti su due piani paralleli. Le facce che formano la superficie laterale sono rettangoli se il prisma è retto, sono parallelogrammi se il prisma non è retto.
Ci occuperemo principalmente di prismi retti.

Pensa alla stanza in cui ti trovi: non è forse un prisma? Il pavimento e il soffitto sono le basi del prisma, le pareti invece sono le facce laterali.
L’altezza del prisma corrisponde alla distanza tra le due basi. Se il prisma è retto è facile da trovare; se invece il prisma è obliquo, dobbiamo fare qualche calcolo in più e aiutarci con il teorema di Pitagora.

Torniamo a pensare un prisma come la stanza in cui ci troviamo. L’area di base di un prisma è la superficie del pavimento ed è equivalente alla superficie del soffitto. La superficie laterale è la somma delle aree di ciascuna parete. E il volume, sai cos’è? Immagina di riempire la stanza di acqua: quanta ce ne può stare?

Cosa succede invece se affettiamo un prisma retto? Se lo tagliamo con piani paralleli alle basi, le sezioni che otteniamo sono congruenti alle basi del prisma. Se invece lo tagliamo con piani perpendicolari alle basi, troviamo dei rettangoli.

Scopriamo insieme tecniche e formule per calcolare la superficie e il volume di un prisma e impariamo a riconoscere i prismi “più famosi”: parallelepipedo e cubo.

Come si calcola la superficie laterale e totale di un prisma

Proviamo ad aprire un prisma, come se fosse una scatola. Quello che otteniamo è il suo sviluppo piano, cioè l’insieme di tutte le sua facce: è formato dalle due basi e da un certo numero di rettangoli (il numero varia a seconda dei lati del poligono di base) che sono le pareti laterali.

Chiamiamo £$ A_b $£ l’area di base, £$ S_l $£ la superficie laterale e £$ S_{tot} $£ la superficie totale. L’area di base di un prisma dipende dal tipo di prisma che abbiamo di fronte: ripassa le aree dei poligoni!

La superficie laterale di un prisma è la somma delle aree di tutti i rettangoli che formano le sue pareti. Qual è l’area di ciascuno di questi rettangoli? È uguale al prodotto tra un lato del poligono e l’altezza del prisma. Tutta la superficie laterale, quindi, è uguale al prodotto del perimetro del poligono di base per l’altezza del prisma. La superficie laterale, infatti, è un grosso rettangolo che ha per base il perimetro della base del prisma e per altezza l’altezza del prisma.

$$ S_l = \text{perimetro di base} \cdot \text{altezza del prisma} $$

Esempio: un prisma esagonale regolare con lato di base £$ \ell $£ e altezza £$ h $£ ha per superficie laterale £$ S_l = 6 \cdot \ell \cdot h $£.

E come si trova la superficie totale? Basta sommare superficie laterale e area di base.
Attenzione! Ricorda che i prismi sono solidi a due basi, quindi per calcolare la superficie totale, dobbiamo sommare due volte l’area di base.

$$ S_{tot} = 2 A_b + S_l $$

Esempio: la superficie totale del nostro prisma esagonale regolare con lato di base £$ \ell $£ e altezza £$ h $£ è £$ S_{tot} = 2A_b + S_l $£.

Quale unità di misura utilizziamo per queste superfici? Anche se stiamo parlando delle superfici di un solido, siamo sempre di fronte a una superficie, cioè un’area. L’unità di misura che utilizziamo è il metro quadrato, cioè £$ \text{m}^2 $£, con tutti i suoi multipli e sottomultipli. Non c’è niente di nuovo da imparare! Fai attenzione e ricordati di elevare l’unità di misura del risultato al quadrato!

Come si calcola il volume di un prisma

Hai bisogno di una scatola capiente, ma devi riuscire a farla stare nel ripiano del tuo armadio. Come puoi trovare la scatola più adatta? Ti serve sapere come calcolare il suo volume!

Il volume di un prisma indica qual è la sua capacità, cioè quanto può contenere. Per trovare il volume di un prisma qualsiasi di altezza £$ h $£, basta moltiplicare l’area di base del prisma per l’altezza.

$$ V = A_b \cdot h $$

Qual è l’unità di misura per i volumi? Stiamo moltiplicando una superficie (che misuriamo in £$ \text{m}^2 $£) per una lunghezza (l’altezza, che misuriamo in £$ \text{m} $£), quindi moltiplichiamo anche le unità di misura! Il volume si misura in metri cubi, cioè £$ \text{m}^3 $£.

Un prisma particolare: il parallelepipedo

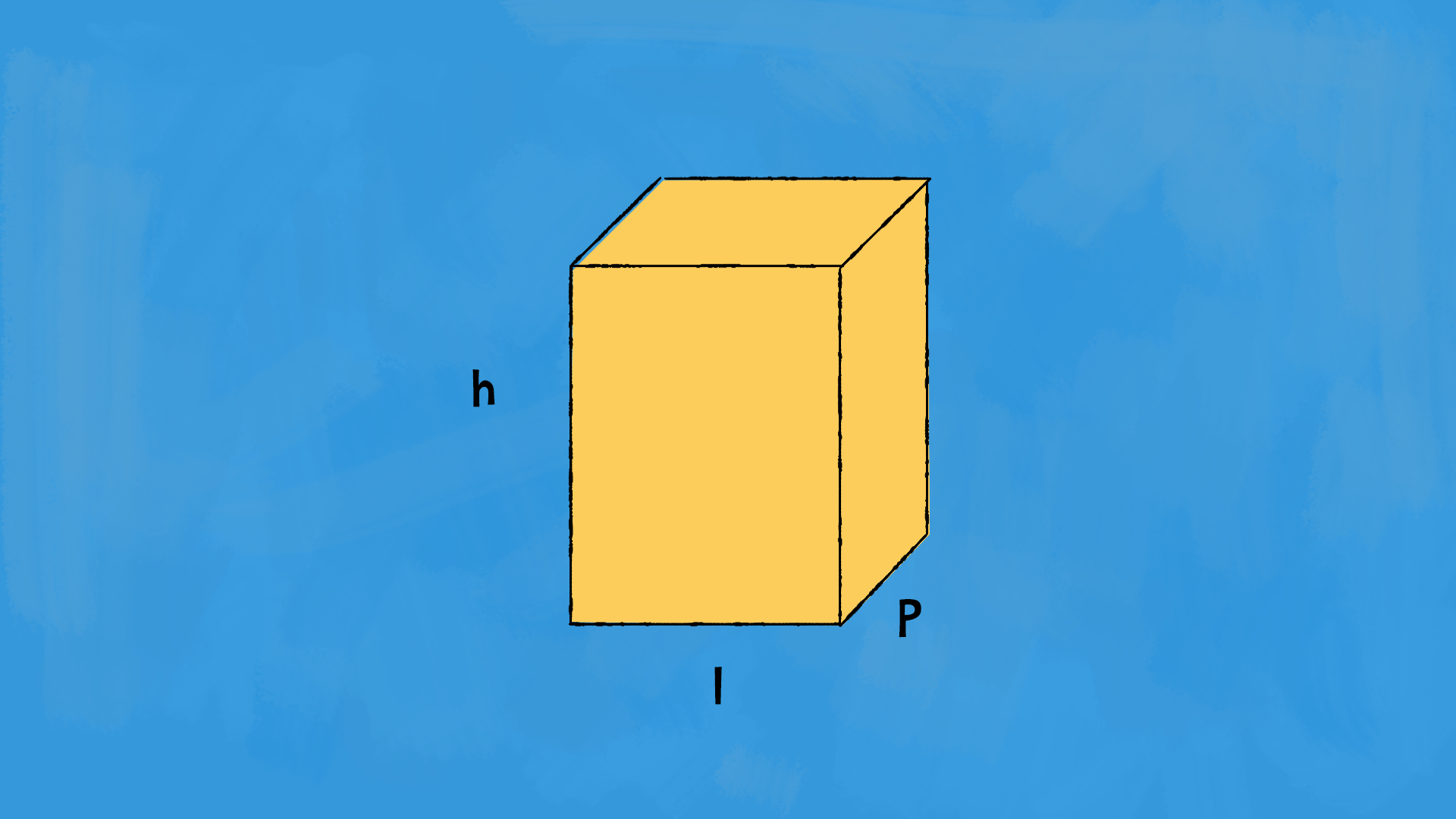
Un prisma particolare è il parallelepipedo. Un parallelepipedo non è altro che un prisma che ha per basi due parallelogrammi!

Diciamo che un parallelepipedo è obliquo se è delimitato da sei parallelogrammi paralleli a due a due; un parallelepipedo è retto se le facce laterali sono rettangolari; un parallelepipedo è rettangolo se tutte le sue facce sono rettangoli.

È un prisma particolare perché è molto facile calcolare la sua superficie e il suo volume. Hai mai notato le misure che vengono specificate nelle descrizioni di scatole, o anche di elettrodomestici come lavatrici, frigoriferi, forni a microonde? Questo perché sono tutti parallelepipedi rettangoli! Tre misure sono sufficienti per capire lo spazio che occupano questi oggetti: larghezza £$(l )$£, altezza £$(h)$£, profondità £$(p)$£. Larghezza e profondità ci indicano le dimensioni della base, poi con l’altezza abbiamo un’idea chiara dello spazio che occupa.

La superficie di base è l’area del rettangolo di base, cioè £$ A_b = l \cdot p $£. La superficie laterale è uguale al perimetro di base per l’altezza, cioè £$ S_l = 2 \cdot (l + p) \cdot h $£. Per calcolare il volume, moltiplichiamo l’area di base per l’altezza: £$ V = A_b \cdot h $£ equivale a moltiplicare le tre dimensioni del parallelepipedo £$ V = l \cdot p \cdot h $£.

E come facciamo se il parallelepipedo è obliquo? Ci comportiamo come abbiamo fatto per i prismi obliqui: basta misurare la distanza tra le due basi per trovare l’altezza… Come facciamo? Ci possiamo aiutare con il teorema di Pitagora!

Il prisma con le facce quadrate: il cubo

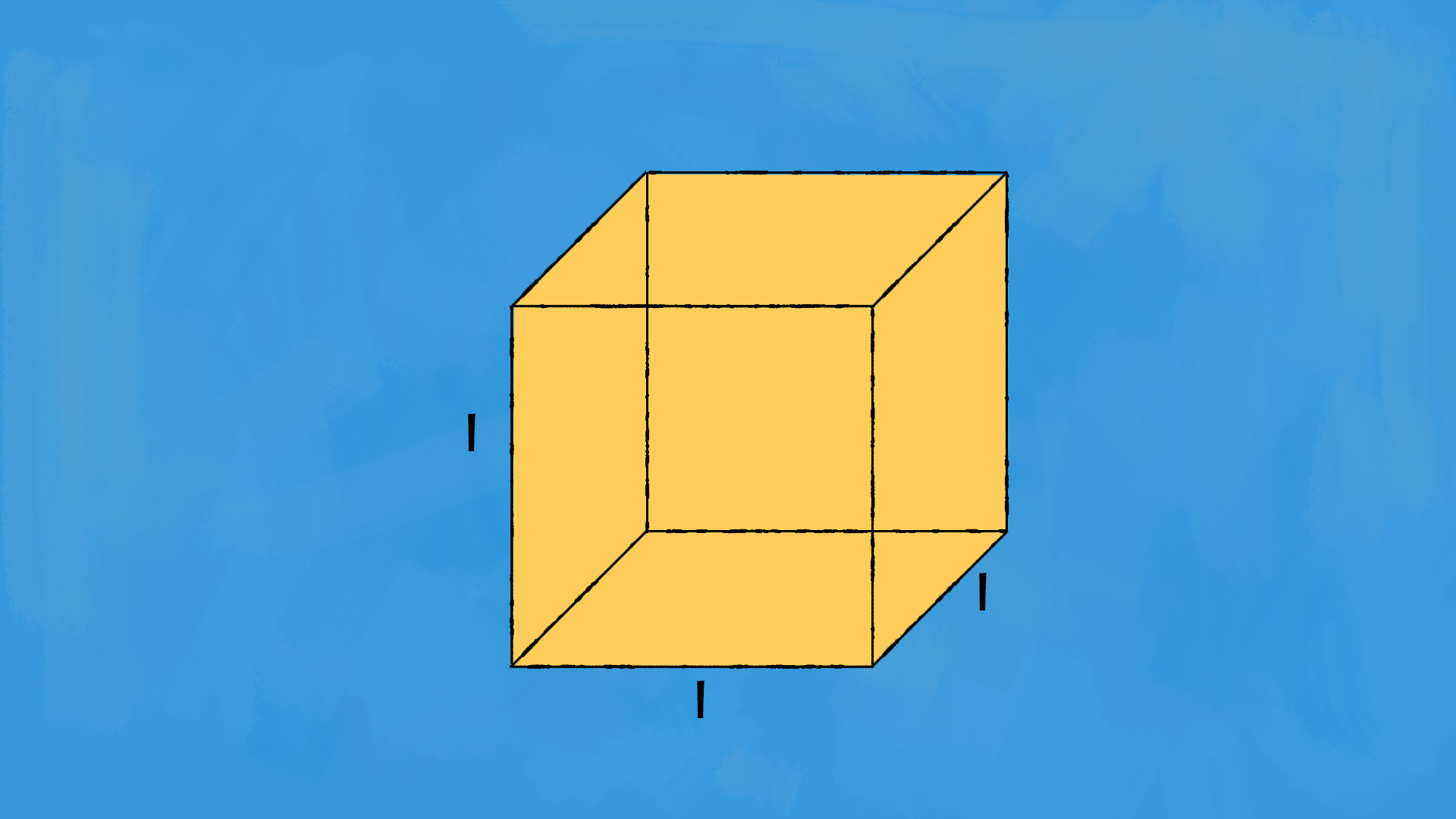
Che tipo di prisma abbiamo davanti se tutte le facce sono dei quadrati? Si tratta di un cubo! Un cubo è un poliedro regolare: si chiama esaedro. È un prisma con sei facce congruenti, tutte quadrate.

Calcolare la superficie di un cubo è un gioco da ragazzi! Basta conoscere il lato di base £$ \ell $£. La sua superficie laterale è formata da quattro quadrati, quindi è £$ S_l = 4 \cdot \ell^2 $£. La sua superficie totale è formata quindi da sei quadrati, la troviamo semplicemente £$ S_{tot} = 6 \cdot \ell^2 $£.

Come calcoliamo il volume di un cubo? Basta moltiplicare il lato di base per tre volte: £$ V = \ell^3 $£.