Prerequisiti per imparare le rette nel piano cartesiano
I prerequisiti per imparare le rette nel piano cartesiano sono:
Caricamento in corso...
Rette nel piano cartesiano
Sul piano cartesiano possiamo disegnare anche rette. Ripasso di segmenti e figure sul piano cartesiano
Appunti
Come facciamo a individuare le rette su piano cartesiano?
Tutte le rette sul piano cartesiano hanno una loro equazione unica: rappresenta la relazione che esiste tra le coordinate £$ x $£ e £$ y $£ di tutti i punti che formano la retta.
Ripassa segmenti e figure sul piano cartesiano
Impara tutto quello che c’è da sapere per disegnare le rette nel piano cartesiano!
Contenuti di questa lezione su: Rette nel piano cartesiano
Rette nel piano cartesiano
Rette orizzontali
Rette verticali
Rette per l'origine
Oltre a punti, segmenti e poligoni, possiamo rappresentare sul piano cartesiano anche le rette.
Individuiamo i punti con le coordinate, i segmenti con le coordinate degli estremi e i poligoni con le coordinate di tutti i vertici. Come si individuano le rette sul piano cartesiano? Serve un’equazione!
Le rette orizzontali rappresentano tutti i punti con la stessa ordinata, quindi hanno equazione £$ y = k $£ con £$ k $£ numero qualsiasi (intero o razionale). Le rette orizzontali sono tutte parallele all’asse £$ x $£ che rappresenta tutti i punti con ordinata uguale a £$ 0 $£: è la retta che passa per l’origine e ha equazione £$ y = 0 $£.
Le rette verticali rappresentano tutti i punti con la stessa ascissa, quindi hanno equazione £$ x = k $£ con £$ k $£ numero qualsiasi (intero o razionale). Le rette verticali sono tutte parallele all’asse £$ y $£ che rappresenta tutti i punti con ascissa uguale a £$ 0 $£: è la retta che passa per l’origine e ha equazione £$ x = 0 $£.
Le rette rappresentano una relazione particolare tra due numeri: lo scopriremo studiando la proporzionalità diretta! La retta che rappresenta tutti i multipli di £$ 2 $£, quindi tutti i punti di coordinate £$ (x_P; 2x_P) $£, è la retta passante per l’origine con equazione £$ y = 2x $£.
Ripasso segmenti nel piano cartesiano
Segmenti orizzontali e verticali
Teorema Pitagora sul piano cartesiano
Esercizio svolto: distanza tra due punti
Il piano cartesiano è un normalissimo piano, solo che ha un sistema di riferimento tale per cui riusciamo a individuare la posizione dei punti e delle figure disegnate sul piano.
Abbiamo già parlato delle coordinate dei punti: due numeri, il primo indica la posizione lungo l’asse £$ x $£ (o asse delle ascisse), il secondo indica la posizione lungo l’asse £$ y $£ (o asse delle ordinate).
Congiungendo due punti qualsiasi £$ A(x_A; y_A) $£ e £$ B(x_B; y_B) $£ sul piano cartesiano troviamo un segmento £$ AB $£. Come facciamo a calcolare la lunghezza di un segmento nel piano cartesiano?
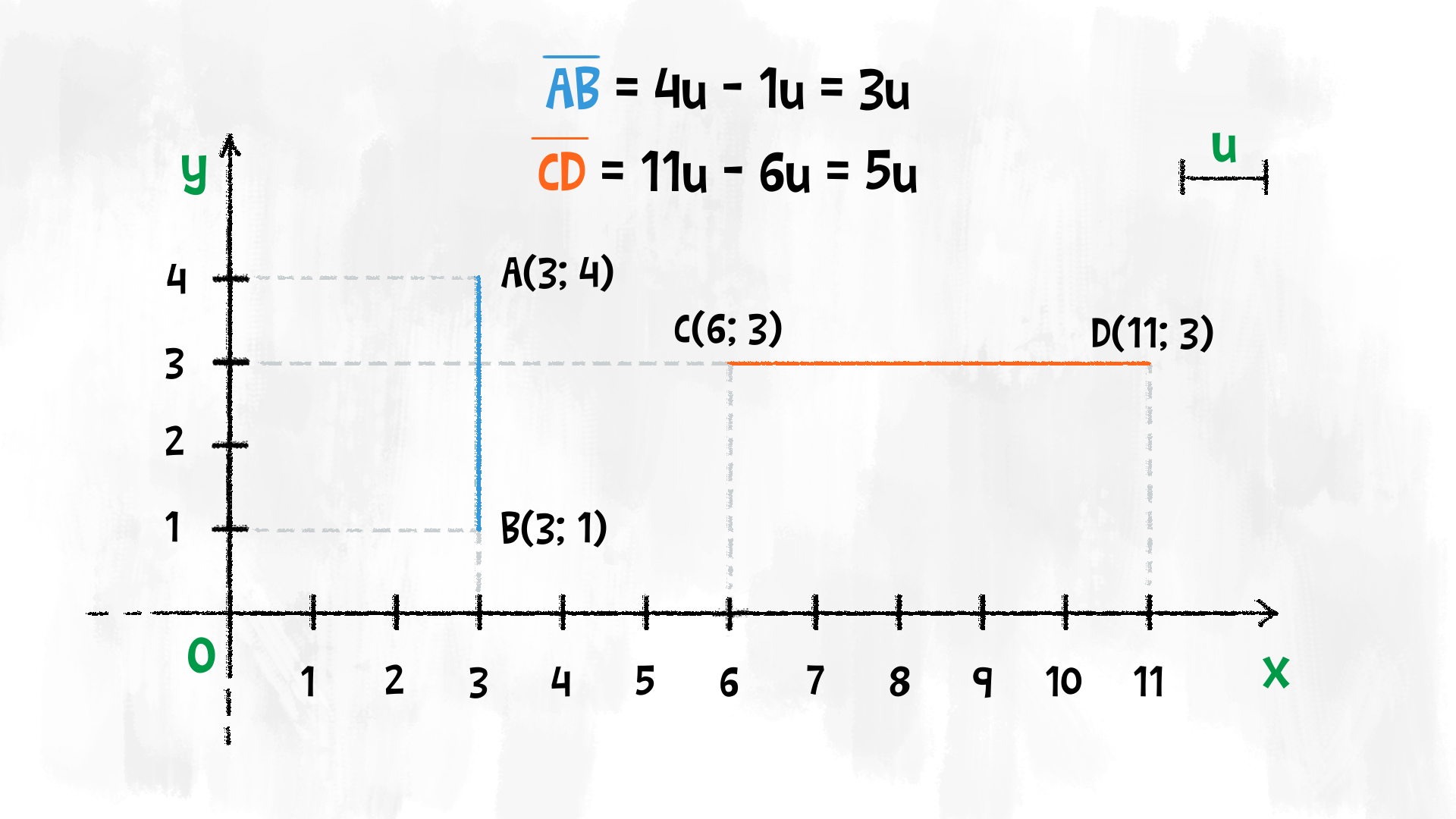
- Se i due estremi hanno la stesso ascissa, si tratta di un segmento verticale: possiamo calcolare la sua lunghezza con una semplice differenza tra le ordinate. Se £$ y_B > y_A $£, troviamo che il segmento ha lunghezza £$ \overline{AB} = y_B - y_A $£, altrimenti viceversa.
- Se i due estremi hanno la stessa ordinata, si tratta di un segmento orizzontale: possiamo calcolare la sua lunghezza con una semplice differenza tra le ascisse. Se £$ x_B > x_A $£, troviamo che il segmento ha lunghezza £$ \overline{AB} = x_B - x_A $£, altrimenti viceversa.
E come facciamo se siamo di fronte ad un segmento che non è né verticale né orizzontale? Qui viene in nostro aiuto il teorema di Pitagora. Possiamo costruire sul piano cartesiano un triangolo rettangolo avente come ipotenusa il segmento £$ AB $£. Quanto misurano i due cateti? Costruiamo il cateto orizzontale che misura £$ x_B - x_A $£ e il cateto verticale che misura £$ y_B - y_A $£. Applichiamo quindi il teorema di Pitagora e troviamo la lunghezza del segmento £$ AB $£:
$$ \overline{AB} = \sqrt{(x_B - x_A)^2 + (y_B - y_A)^2} $$
Ripasso poligoni nel piano cartesiano
Aree nel piano cartesiano
Esercizio svolto
Sul piano cartesiano possiamo disegnare punti, segmenti e anche poligoni: basta congiungere più segmenti a formare una linea spezzata chiusa.
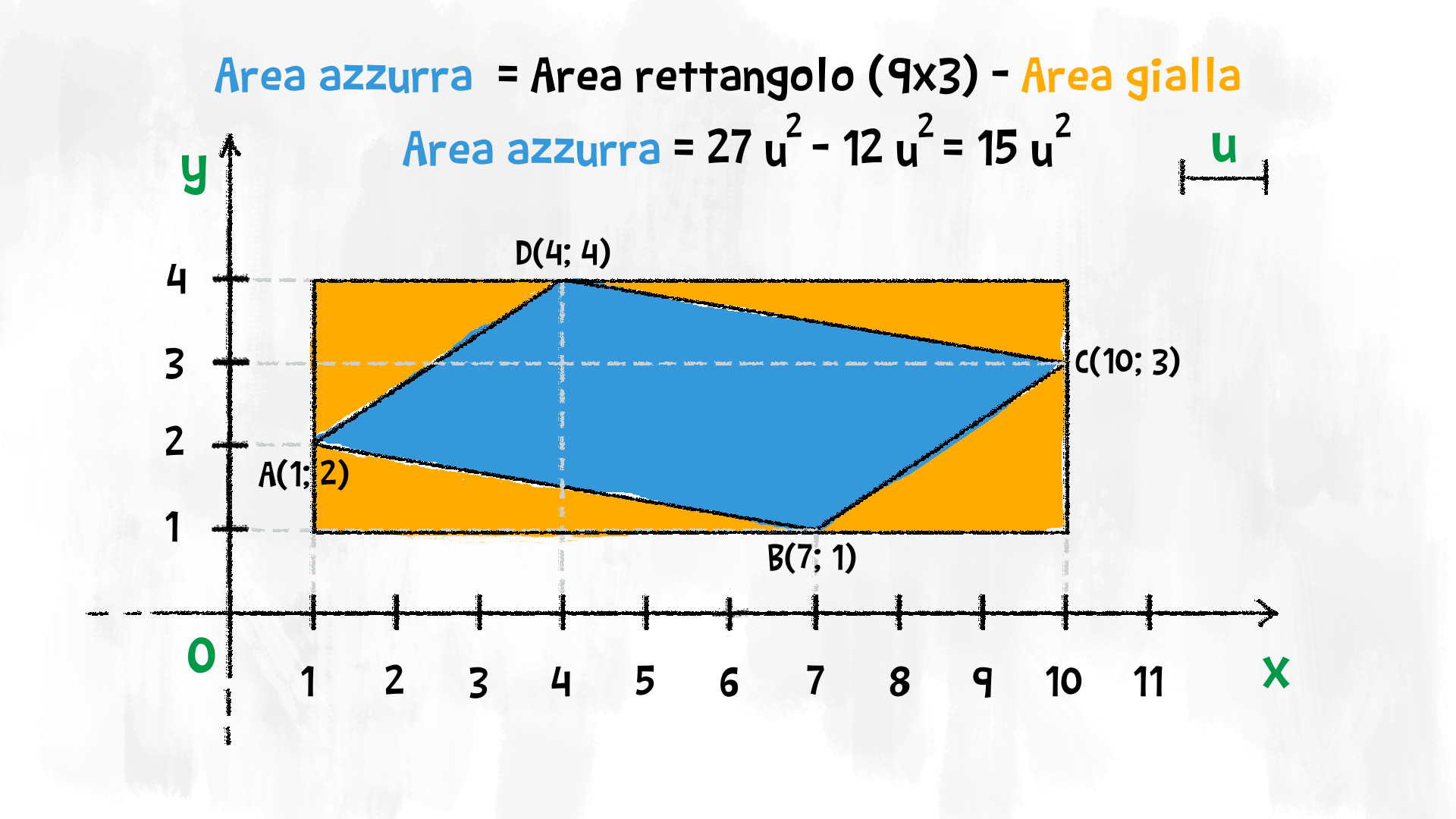
Possiamo calcolare il perimetro e l’area di un poligono sul piano cartesiano, come abbiamo già imparato a fare. Per trovare il perimetro, dobbiamo calcolare le lunghezze di tutti i segmenti e sommarle. Per calcolare l’area, possiamo aiutarci costruendo sul piano cartesiano delle figure di cui conosciamo l’area, e poi trovare le aree della figura che stiamo cercando.
Abbiamo imparato che i segmenti di cui è più facile trovare la lunghezza sono quelli orizzontali e verticali. Per calcolare l’area di una figura strana sul piano cartesiano, troviamo il rettangolo che la racchiude e arriviamo all’area finale sottraendo le aree dei triangoli o delle altre figure che riusciamo a riconoscere.
