I parallelogrammi: come calcolare il perimetro
Un parallelogramma è un quadrilatero formato da due coppie di lati paralleli. Tra i parallelogrammi riconosciamo i rettangoli, i rombi e i quadrati. Scopri tutte le proprietà di questi poligoni e impara come calcolare il perimetro di tutti i parallelogrammi.
Il termine “parallelogramma” significa “linea parallela”. Infatti un parallelogramma è una figura di quattro lati, paralleli e congruenti a due a due.
I parallelogrammi costituiscono un sottoinsieme dei trapezi e sono le forme che incontriamo più spesso nella vita di tutti i giorni: lo schermo dello smartphone o del computer, il campo da basket, o anche i pannelli solari che stanno sui tetti delle case!
Impara a riconoscere in questo articolo tutti i parallelogrammi e scopri tutte le loro proprietà!
Che cosa sono i parallelogrammi
Proprietà del parallelogramma

Perimetro del parallelogramma
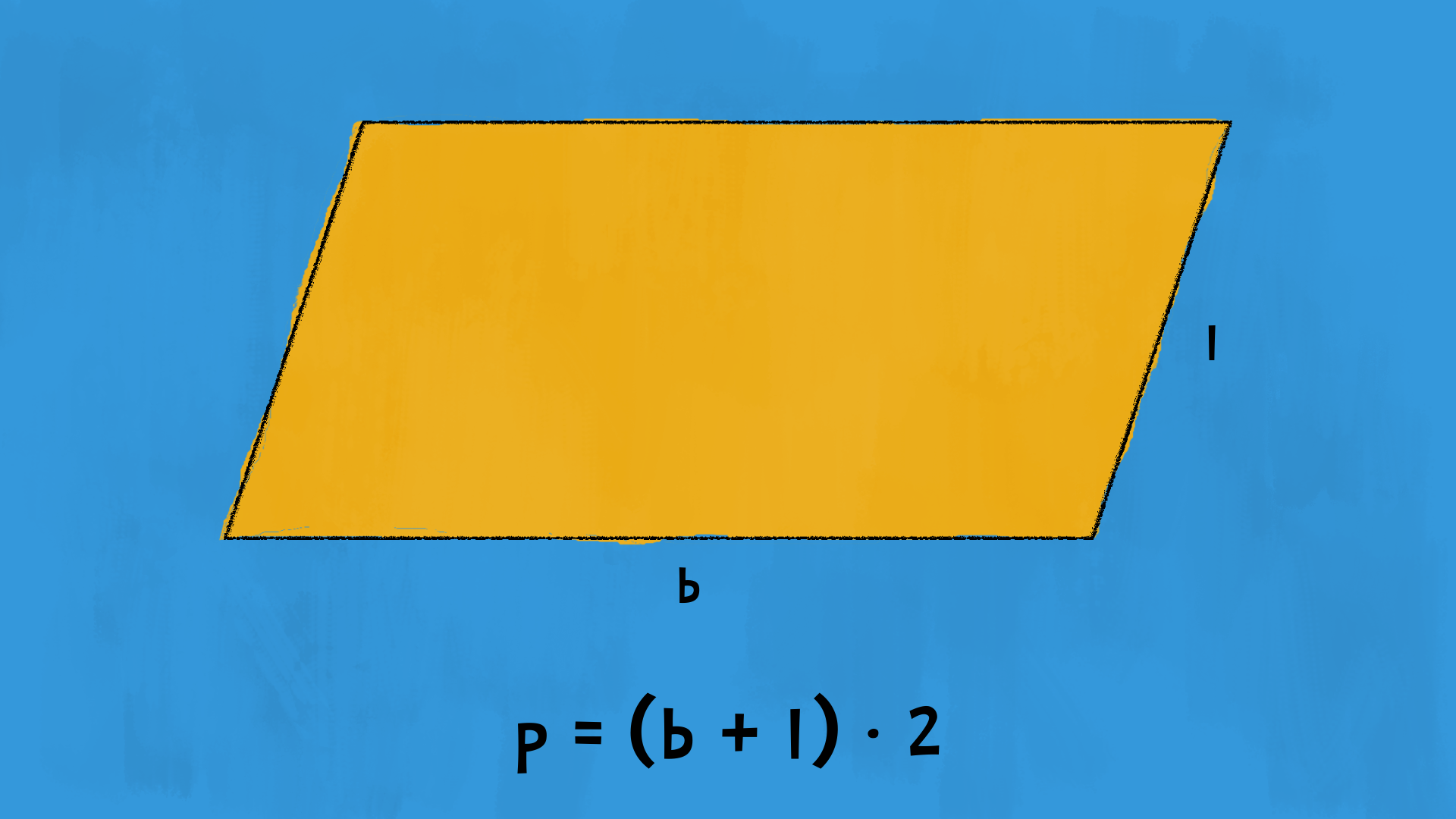
Tra tutti i poligoni con quattro lati, ce ne sono alcuni che hanno delle caratteristiche particolari: i parallelogrammi.
Il termine parallelogramma significa “linea parallela”, infatti un parallelogramma è un quadrilatero con i lati opposti paralleli e congruenti.
Anche gli angoli opposti di un parallelogramma sono congruenti. Gli angoli adiacenti a ciascun lato, invece, sono supplementari: la loro somma è uguale ad un angolo di £$ 180^\circ $£. Visto che i lati opposti di un parallelogramma sono paralleli, valgono le proprietà delle parallele tagliate da una trasversale: gli angoli coniugati interni sono supplementari!
Un’altra proprietà interessante riguarda le diagonali: ogni parallelogramma ha due diagonali che si intersecano nel loro punto medio.
Per i lati di un parallelogramma, parliamo di base e lato obliquo: basta indicare la misura di due lati per avere tutte le informazioni, perché i lati opposti sono paralleli e congruenti. Per calcolare il perimetro di un parallelogramma, basta sommare la misura di una base e di un lato obliquo, quindi moltiplicare per £$ 2 $£:
$$ p = ( b + l ) \cdot 2 $$
Il rombo
Proprietà del rombo
Perimetro del rombo
Anche i parallelogrammi possono essere equilateri. Un parallelogramma con quattro lati congruenti è un rombo. Hai mai sentito parlare del pesce rombo? Questo pesce ha una forma che ricorda questa figura geometrica. 😉
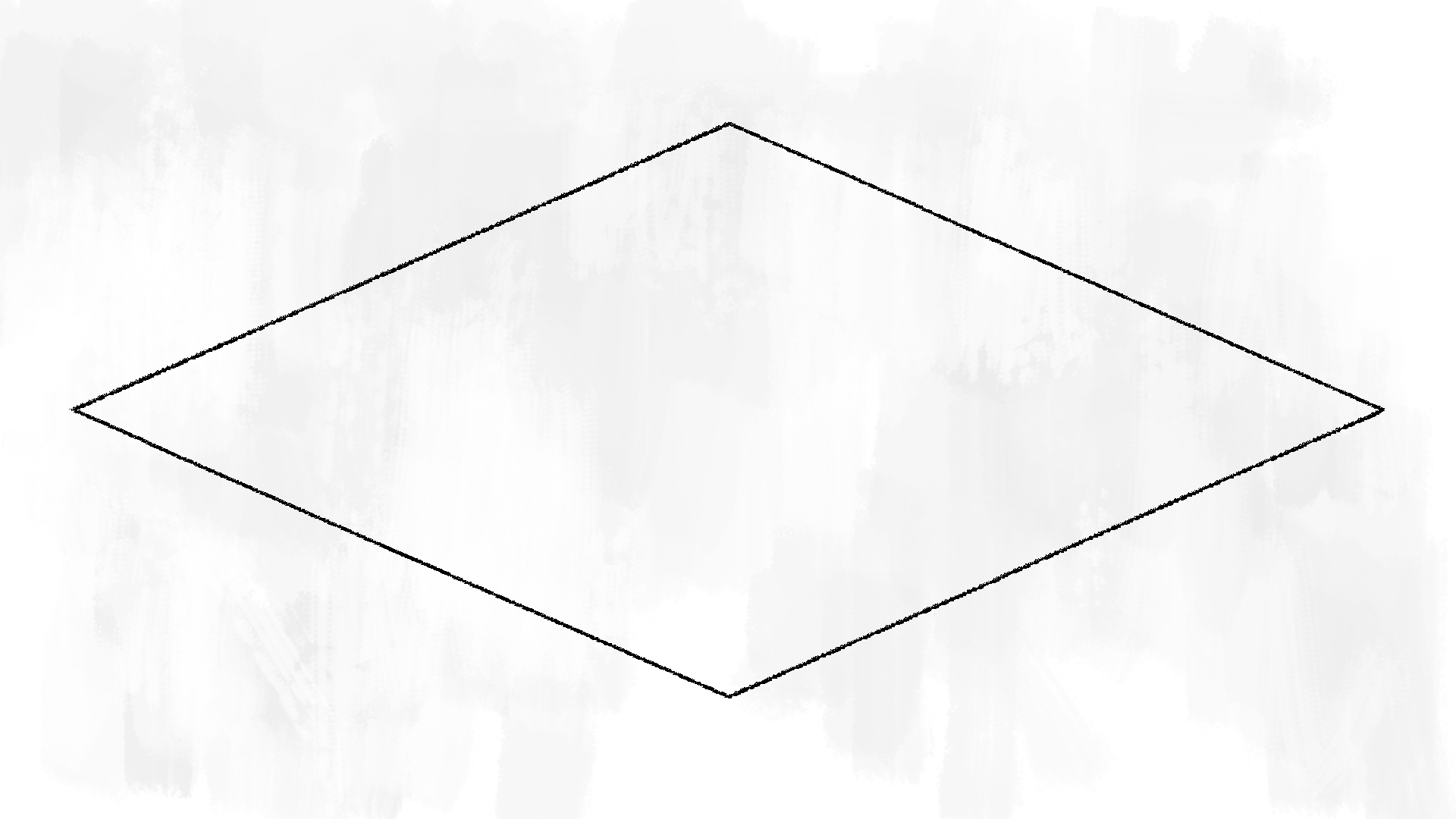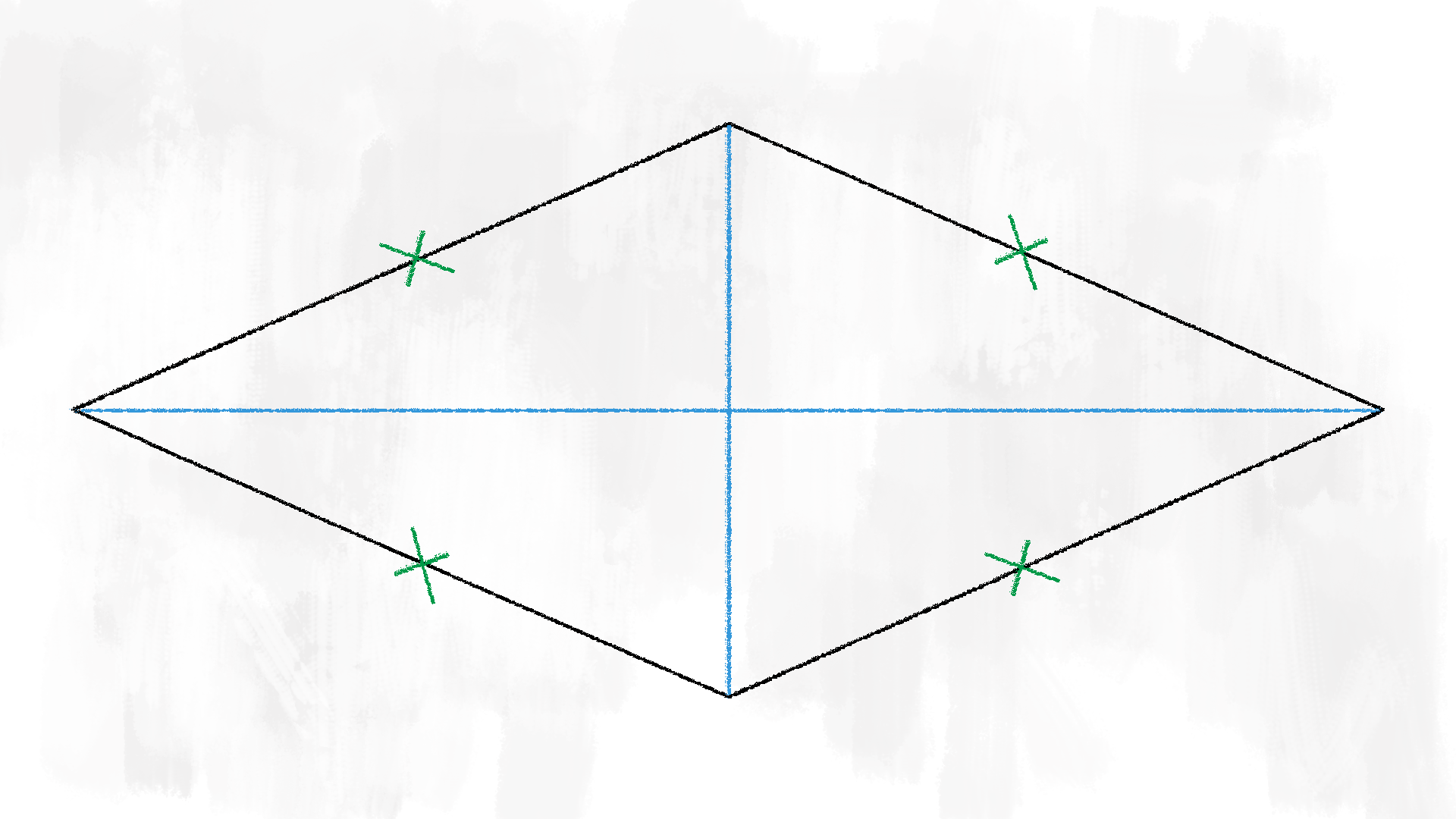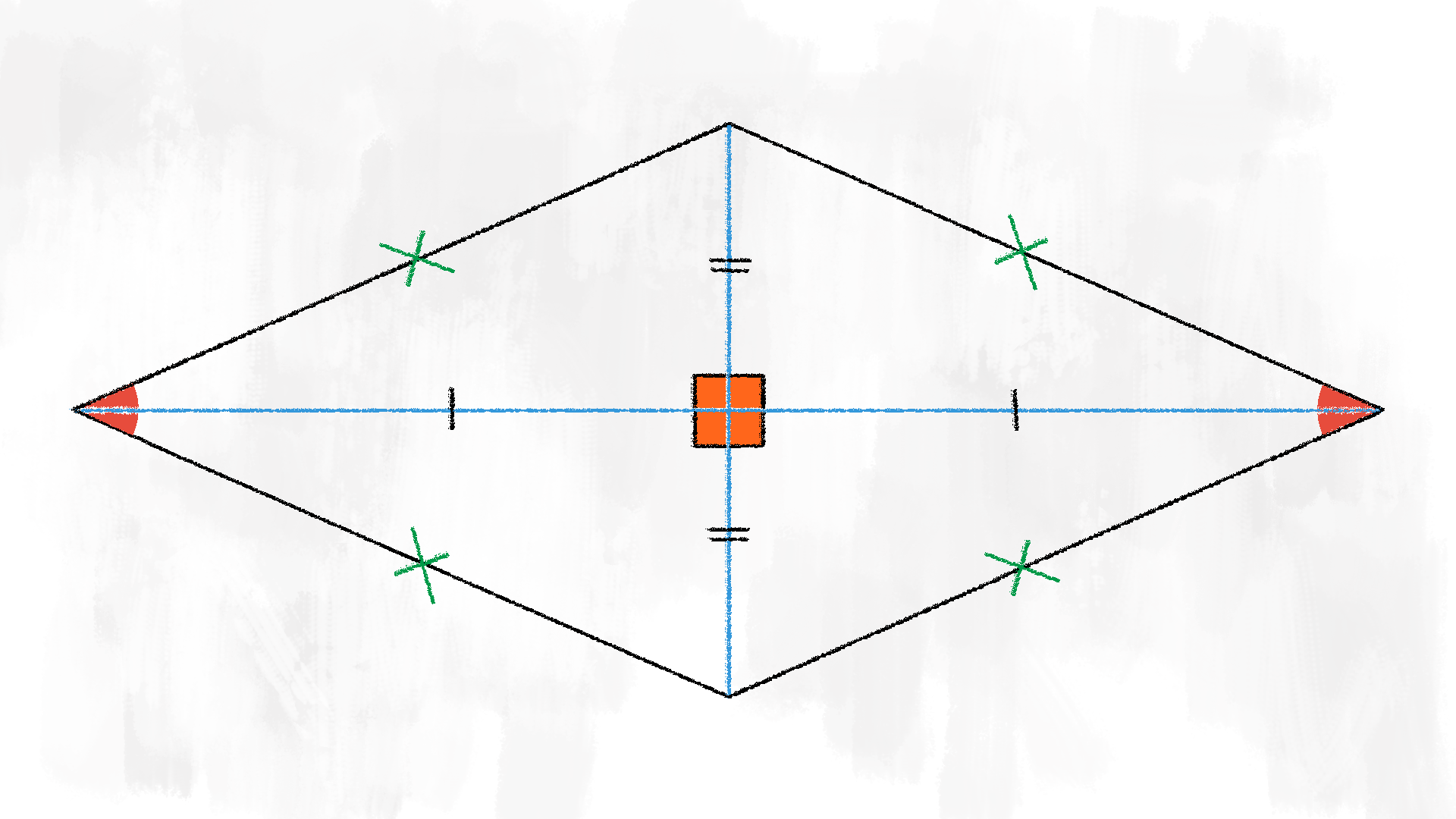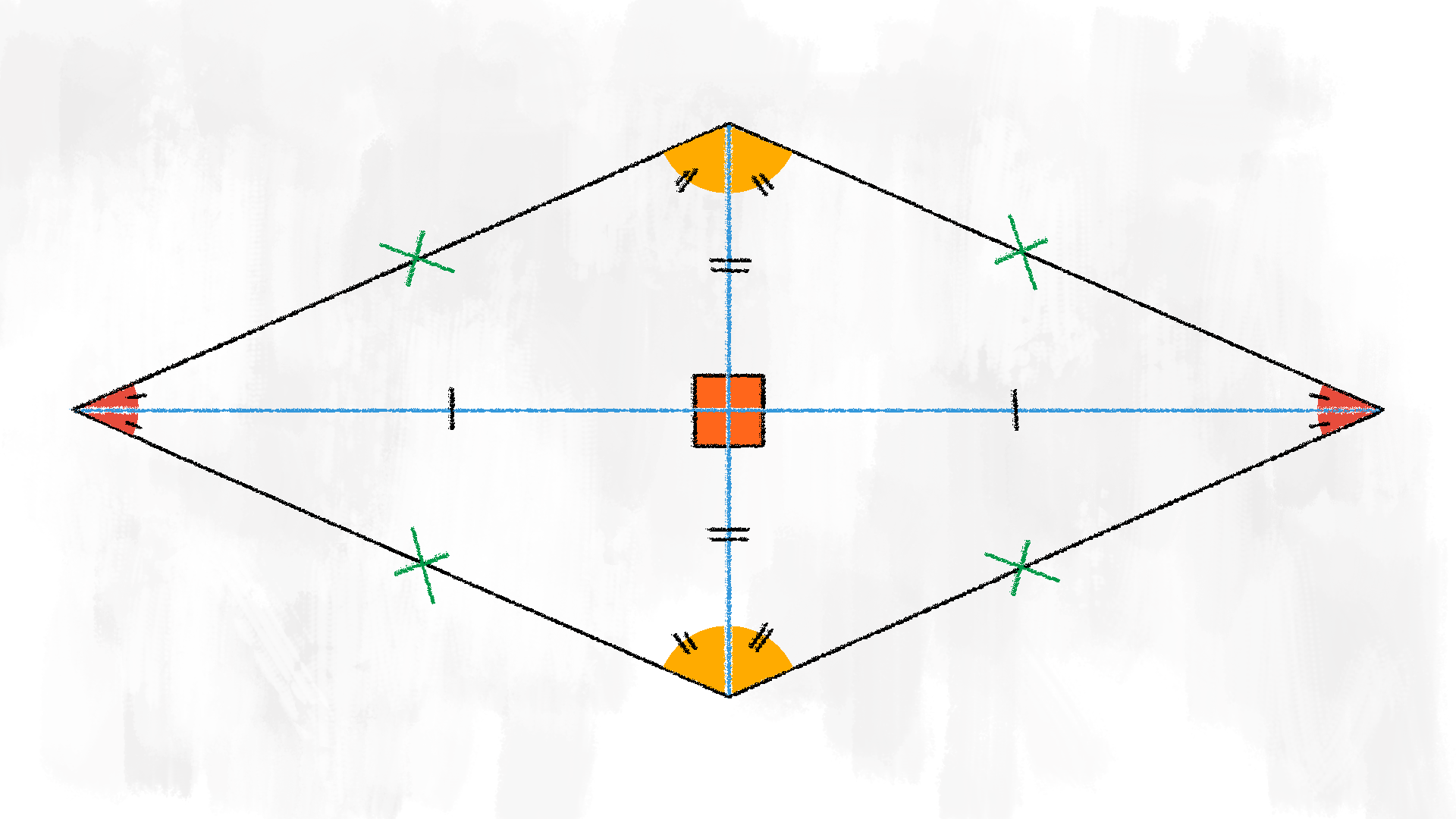
Il rombo ha tutte le caratteristiche di cui abbiamo già parlato per i parallelogrammi, quindi gli angoli opposti congruenti, i lati opposti paralleli, ma, in più, i quattro lati sono congruenti. Le diagonali del rombo sono anche le bisettrici dei quattro angoli. Si intersecano nel loro punto medio e sono perpendicolari tra loro: tracciate le due diagonali del rombo, questo risulta diviso in quattro triangoli rettangoli, tutti congruenti tra loro.
Nel rombo le due diagonali non sono congruenti: distinguiamo la
diagonale maggiore e la diagonale minore.
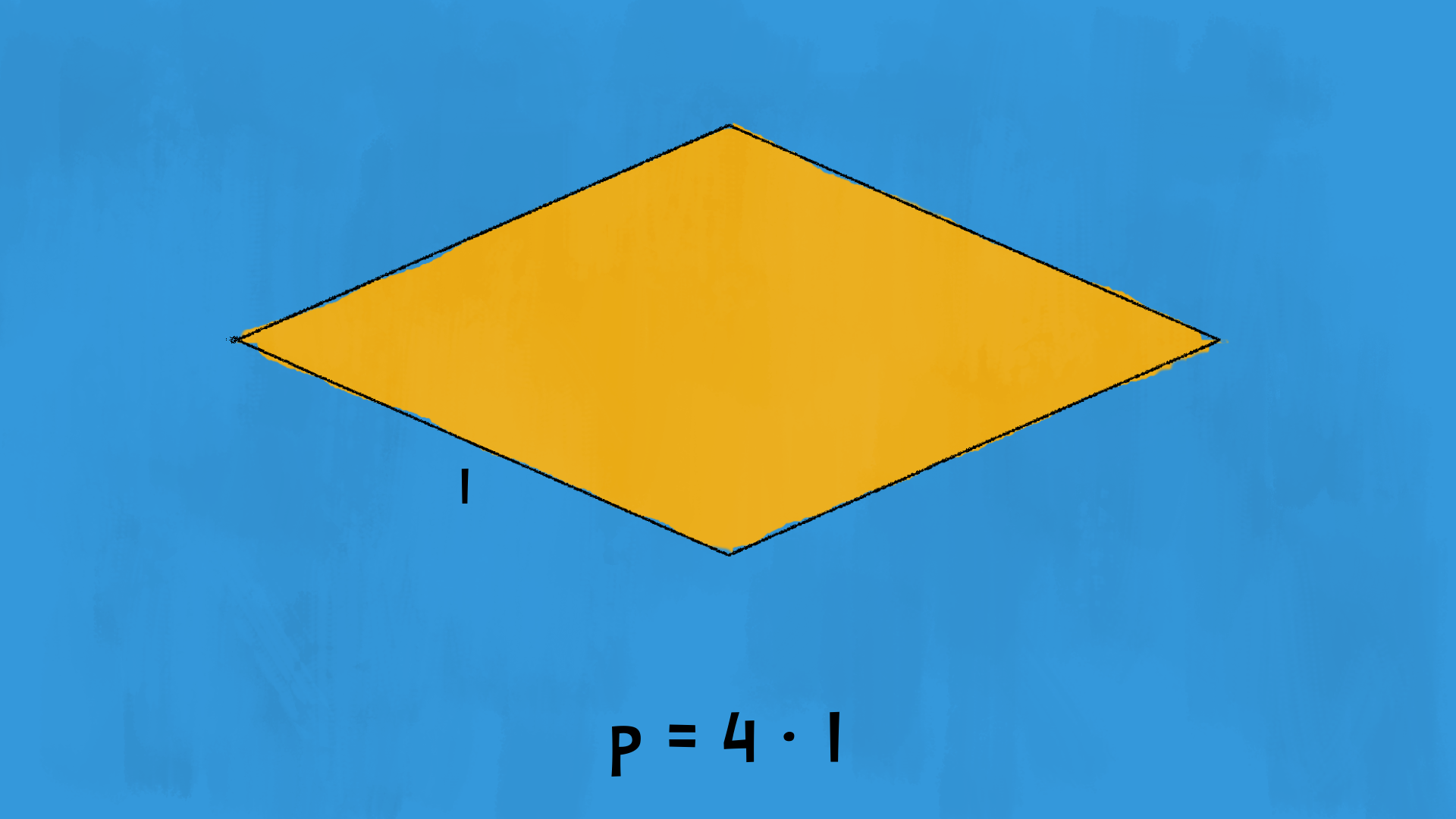
Calcolare il perimetro del rombo è facile: conoscendo la misura di un lato, possiamo trovare il perimetro moltiplicandola per £$ 4 $£:
$$ p = 4 \cdot l $$
Il rettangolo
Proprietà del rettangolo

Perimetro del rettangolo
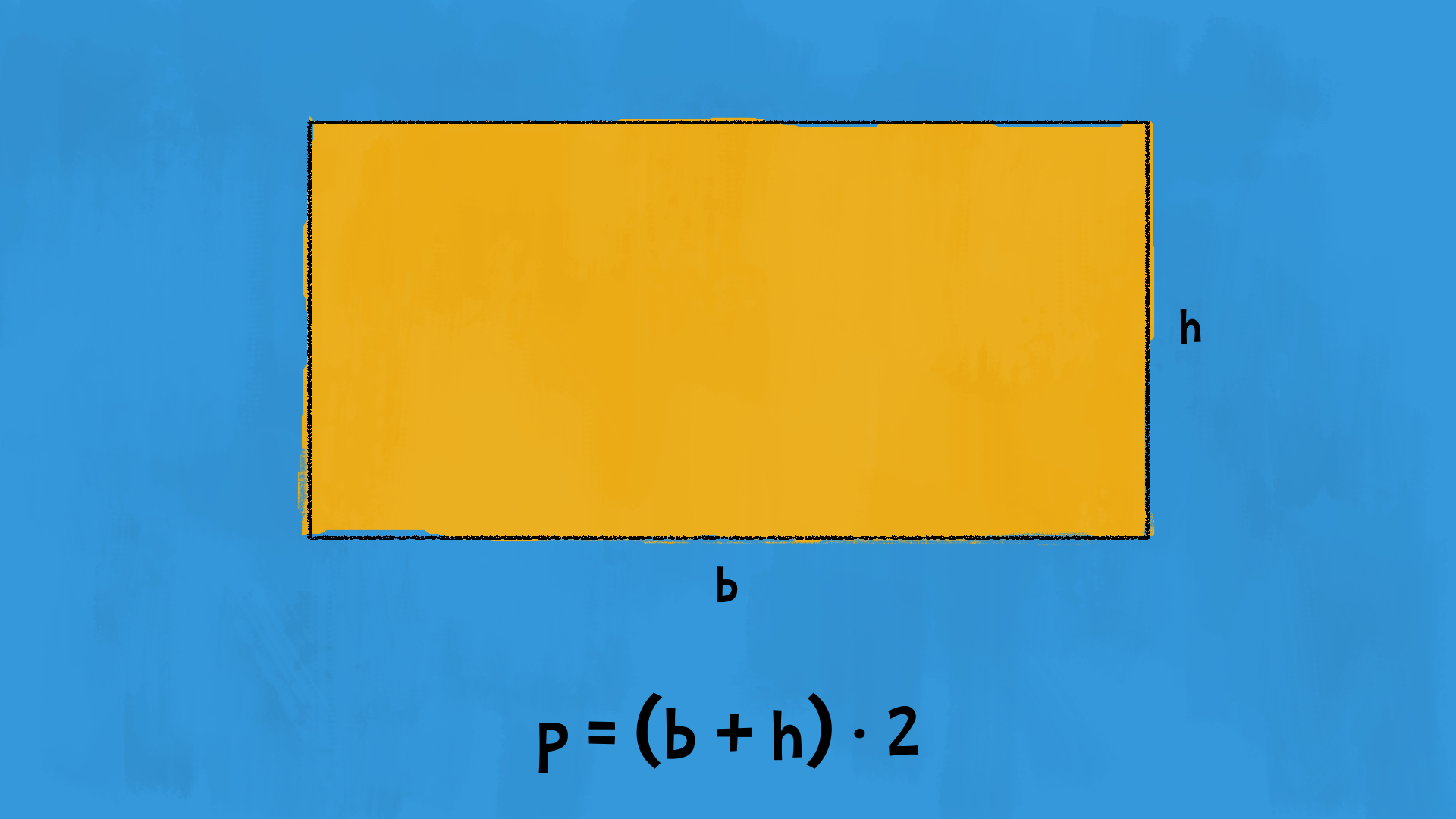
Un parallelogramma equiangolo è un rettangolo. Un rettangolo è un poligono con quattro angoli retti, come si intuisce dal suo nome.
Le diagonali del rettangolo si intersecano nel loro punto medio. Le due diagonali del rettangolo sono congruenti.
Anche con quattro angoli retti, questo poligono resta sempre un parallelogramma, cioè un quadrilatero con i lati opposti paralleli e congruenti. Chiamiamo i lati orizzontali congruenti basi £$( b )$£ e i lati verticali altezze £$ ( h ) $£.
Per calcolare il perimetro del rettangolo, procediamo come per un generico parallelogramma: sommiamo la base e l’altezza e poi moltiplichiamo per £$ 2 $£:
$$ p = (b + h) \cdot 2 $$
Il quadrato
Proprietà del quadrato

Perimetro del quadrato
Un parallelogramma equilatero ed equiangolo è un quadrato. Un quadrato è un poligono con quattro lati congruenti e quattro angoli retti. Un quadrato è un poligono regolare!
In inglese indichiamo questo poligono con il termine square, che però significa anche piazza. Ci hai mai fatto caso? La piazza era orginariamente un luogo aperto dedicato al commercio che si trovava all’incrocio di quattro strade: aveva proprio la forma di un quadrato!
Come per i rettangoli, le diagonali del quadrati sono congruenti e si intersecano nel loro punto medio. Come per i rombi, le diagonali sono perpendicolari e sono le bisettrici dei quattro angoli.
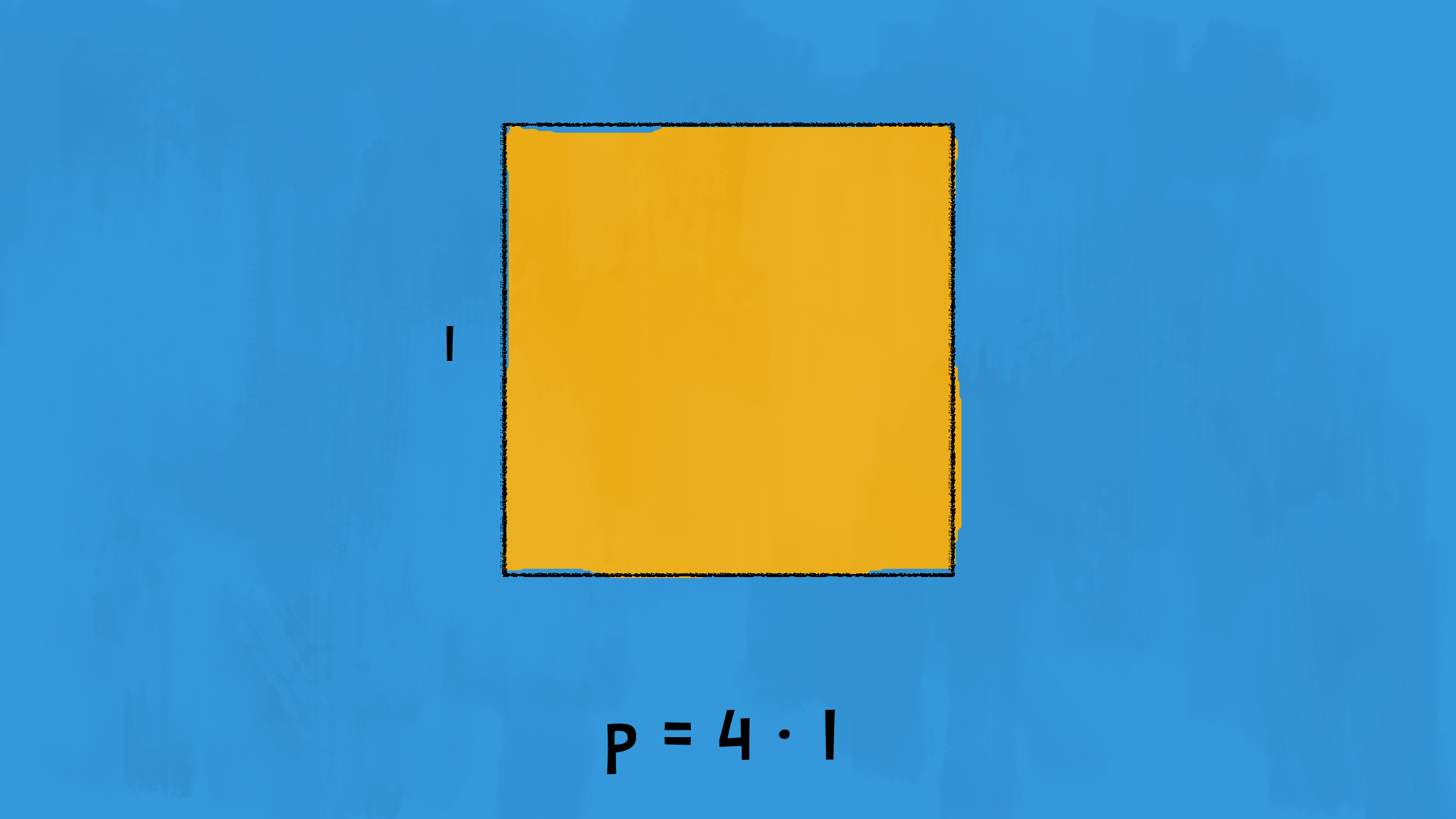
Per calcolare il perimetro del quadrato, procediamo come per il rombo: moltiplichiamo per £$ 4 $£ la misura del lato.
$$ p = 4 \cdot l $$
