Triangoli 30-60-90: le formule applicate
Il triangolo 30°, 60°, 90° è un triangolo rettangolo particolare. Al primo sguardo, può apparire come qualsiasi altro triangolo, ma la sua struttura interna nasconde un insieme di proprietà che lo rendono unico. Come suggerisce il nome, questo triangolo ha angoli interni misuranti rispettivamente 30, 60 e 90 gradi. La presenza di un angolo retto lo classifica come un triangolo rettangolo, ma quello che lo distingue dagli altri triangoli rettangoli sono gli angoli acuti rimanenti e le proporzioni tra i suoi lati.
L’origine di questo triangolo può essere rintracciata nel triangolo equilatero, un triangolo in cui tutti gli angoli misurano 60 gradi e tutti i lati hanno la stessa lunghezza. Tracciando l’altezza relativa a uno dei tre lati di un triangolo equilatero, riusciamo a dividerlo in due triangoli rettangoli che hanno caratteristiche particolari. Oltre all’angolo retto hanno un angolo da £$ 30^\circ $£ e uno da £$ 60^\circ $£. Uno dei due cateti è lungo quanto metà dell’ipotenusa. E quanto misura l’altro? Applicando il teorema di Pitagora, compare un altro numero irrazionale nei nostri calcoli: £$ \sqrt 3 $£.
Ma non preoccuparti, vedremo insieme passo passo quali sono le sue caratteristiche e come è possibile applicare il teorema di Pitagora!
Il triangolo 30°, 60°, 90°
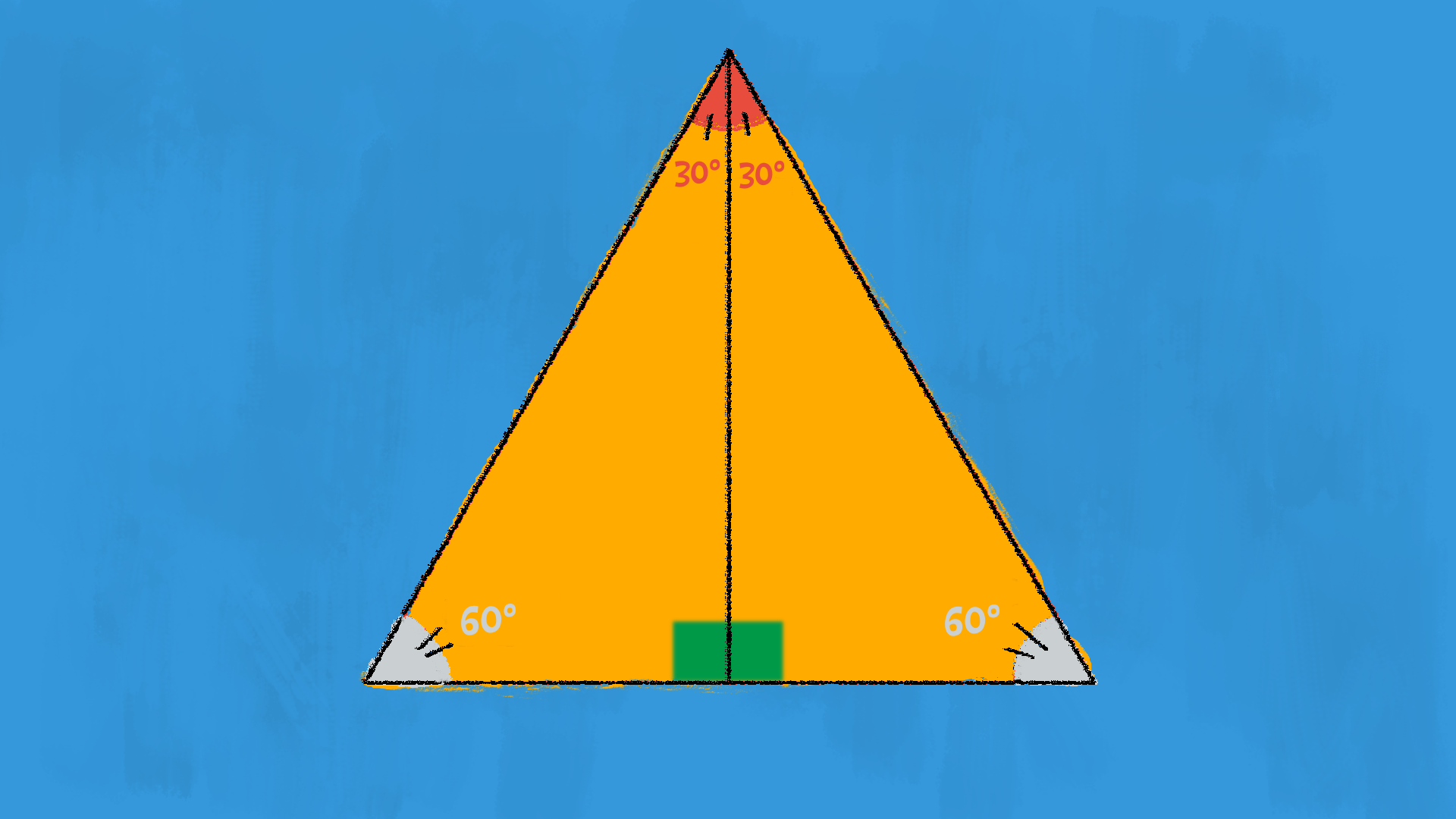
Prendiamo un triangolo equilatero: si tratta di un poligono regolare, con tutti i lati e tutti gli angoli uguali. Se tracciamo l’altezza relativa ad uno dei tre lati, dividiamo il triangolo in due triangoli rettangoli. Infatti l’altezza è il segmento perpendicolare che congiunge il vertice al lato opposto. Ma come sono fatti questi due triangoli?
Sappiamo che in un triangolo equilatero, le altezze, le mediane e le bisettrici relative a ciascun lato, coincidono! Allora quello che otteniamo è un triangolo un po’ particolare:
- l’altezza che tracciamo è anche bisettrice, quindi divide a metà l’angolo al vertice;
- l’altezza che tracciamo è anche mediana, quindi divide a metà il lato opposto;
- l’altezza, per le sue proprietà, è perpendicolare al lato opposto al vertice da cui parte.
Visto che il triangolo equilatero ha tre angoli uguali, cioè di £$ 60^\circ $£, grazie alle proprietà che abbiamo appena elencato, tracciando un’altezza ricaviamo un triangolo rettangolo che:
- oltre all’angolo retto, ha un angolo di £$ 60^\circ $£ e un angolo di £$ 30^\circ $£;
- ha il cateto minore lungo come la metà dell’ipotenusa.
Tagliando a metà un triangolo equilatero otteniamo un triangolo £$ 30^\circ $£, £$ 60^\circ $£, £$ 90^\circ $£!
Come la squadretta che utilizzi per il disegno tecnico: è un triangolo rettangolo con un angolo da £$ 30^\circ $£ e uno da £$ 60^\circ $£.
La radice quadrata di 3: £$ \sqrt 3 $£
Proviamo ad applicare il teorema di Pitagora alla metà di un triangolo equilatero con i lati da £$ 2 \text{ cm} $£. Sappiamo quindi che l’ipotenusa £$ ( i ) $£ del triangolo da £$ 30^\circ $£, £$ 60^\circ $£, £$ 90^\circ $£ che otteniamo è uguale al lato del triangolo di partenza, quindi misura £$ 2 \text{ cm} $£, mentre il cateto minore £$ (c ) $£ è uguale alla metà del lato (perché l’altezza £$ (h ) $£ che abbiamo tracciato è anche una mediana), quindi misura £$ 1 \text{ cm} $£.
Quanto misura l’altro cateto, cioè l’altezza del triangolo equilatero? Utilizziamo il teorema di Pitagora:
$$ h = \sqrt{i^2 – c^2} = \sqrt{2^2 \text{ cm}^2 – 1^2 \text{ cm}^2} = \\ = \sqrt{3 \text{ cm}^2} = \sqrt 3 \text{ cm} $$
L’altezza di un triangolo equilatero con il lato di £$ 2 \text{ cm} $£ misura £$ \sqrt 3 \text{ cm} $£.
Grazie a questa applicazione del teorema di Pitagora, abbiamo scoperto un altro numero irrazionale: £$ \sqrt 3 $£ è la misura del cateto maggiore di un triangolo rettangolo con angoli di £$ 30^\circ $£, £$ 60^\circ $£, £$ 90^\circ $£, o, meglio ancora, è la misura dell’altezza di un triangolo equilatero con lato che misura due unità.
Le proprietà del triangolo equilatero
Grazie al teorema di Pitagora, abbiamo potuto scoprire la relazione tra il lato e l’altezza di un triangolo equilatero.
Per tutti i triangoli rettangoli che sono la metà di un triangolo equilatero, quindi per tutti i triangoli rettangoli con un angolo di £$ 30^\circ $£ e un angolo di £$ 60^\circ $£ sappiamo che:
- l’ipotenusa è il doppio del cateto minore: £$ i = 2 \cdot c $£;
- il cateto maggiore è £$ \sqrt 3 $£ volte il cateto minore: £$ C = \sqrt 3 c $£.
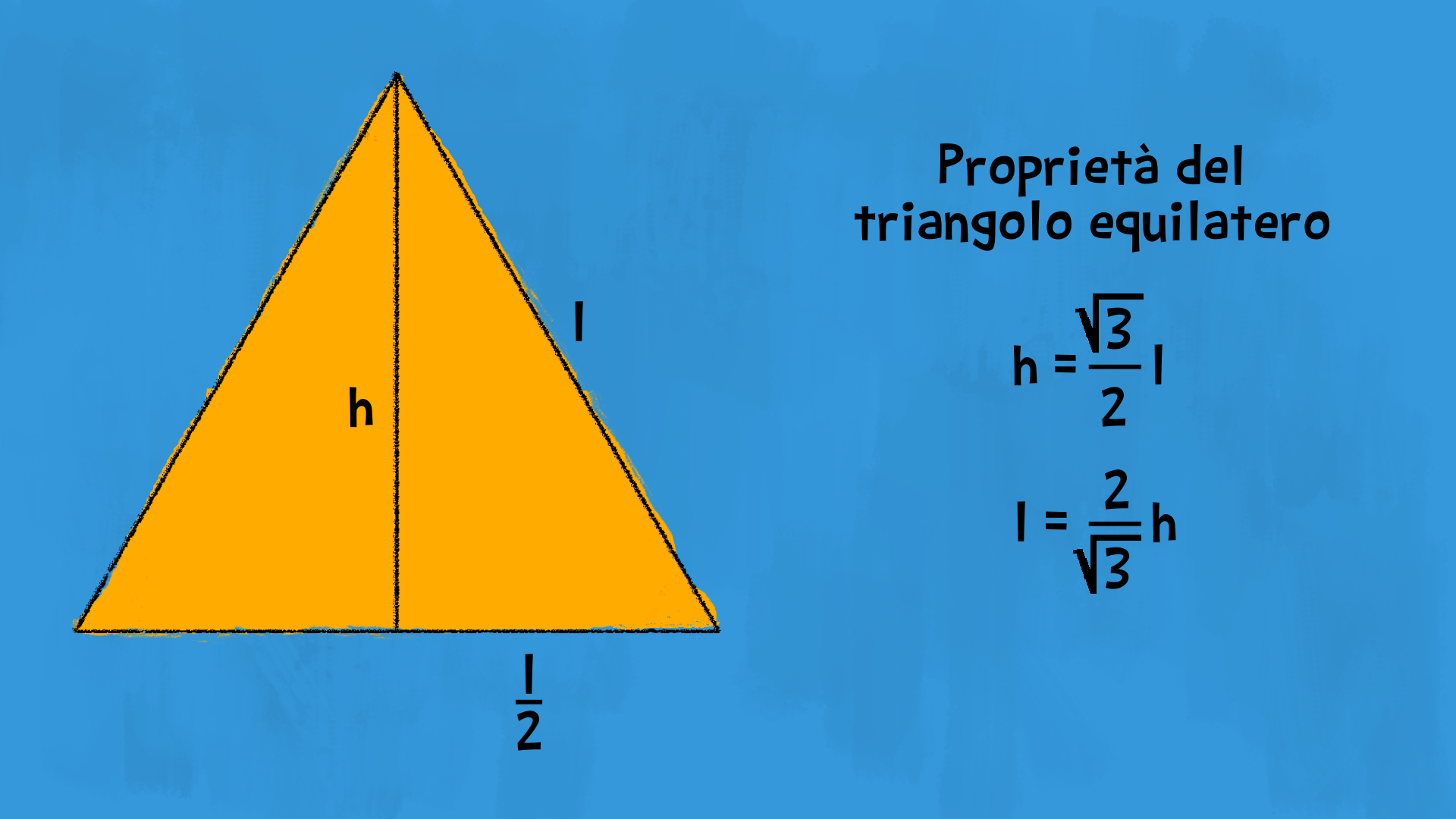
Di conseguenza sappiamo che, in tutti i triangoli equilateri di lato £$ \ell $£, l’altezza è £$ \frac{\sqrt 3}{2} $£ volte il lato: £$ h = \frac{\sqrt 3}{2} \ell $£.
Conoscendo l’altezza, possiamo risalire alla misura del lato del triangolo equilatero sfruttando la relazione inversa: £$ \ell = \frac{2}{\sqrt 3}h $£.
Grazie a questi trucchi, non sarà più necessario applicare il teorema di Pitagora ad un triangolo rettangolo con angoli di £$ 30^\circ $£ e di £$ 60^\circ $£: basta ricordarsi della radice di £$ 3 $£!
