I punti notevoli e le proprietà di un triangolo

I triangoli sono figure chiuse formate da tre lati, tre angoli e tre vertici. La bellezza e la complessità di un triangolo emergono quando iniziamo a esplorare i vari punti notevoli e le loro proprietà. Ad esempio, ogni triangolo ha un baricentro, un punto in cui si intersecano le mediane del triangolo. Le mediane sono segmenti che collegano ciascun vertice con il punto medio del lato opposto. Il baricentro è unico in quanto è il punto in cui il triangolo può essere bilanciato perfettamente.

Un altro punto notevole è l’ortocentro, il punto in cui si incontrano le altezze del triangolo. Le altezze sono i segmenti perpendicolari tracciati da ciascun vertice al lato opposto (o al suo prolungamento). L’ortocentro rivela un aspetto interessante della simmetria e delle proprietà angolari del triangolo.

C’è poi l’incentro, il punto in cui si intersecano le bisettrici degli angoli interni del triangolo. L’incentro è notevole perché è il centro della circonferenza inscritta nel triangolo, una circonferenza che tocca ciascun lato del triangolo in un solo punto.

Infine, abbiamo il circocentro, il punto in cui si intersecano le perpendicolari mediane dei lati. Queste sono le linee perpendicolari tracciate al centro di ciascun lato. Il circocentro è il centro della circonferenza circoscritta al triangolo, una circonferenza che passa per tutti e tre i vertici del triangolo.

Oltre a questi punti notevoli, i triangoli presentano una varietà di proprietà legate ai loro lati e angoli. Ad esempio, la somma degli angoli interni di un triangolo è sempre 180 gradi, e ci sono relazioni specifiche tra i lati e gli angoli in diversi tipi di triangoli (come equilateri, isosceli e scaleni).

Scopriamoli meglio insieme!

• Altezze e ortocentro
• Mediane e baricentro
• Bisettrici e incentro
• Assi e circocentro
• Sfida sui punti notevoli di un triangolo

Altezze e ortocentro

Per disegnare una delle altezze di un triangolo, partiamo da un vertice e tracciamo il segmento perpendicolare al lato opposto.

Nella figura, £$ H $£ è il piede dell’altezza condotta dal vertice £$ C $£ sul lato opposto £$ AB $£.
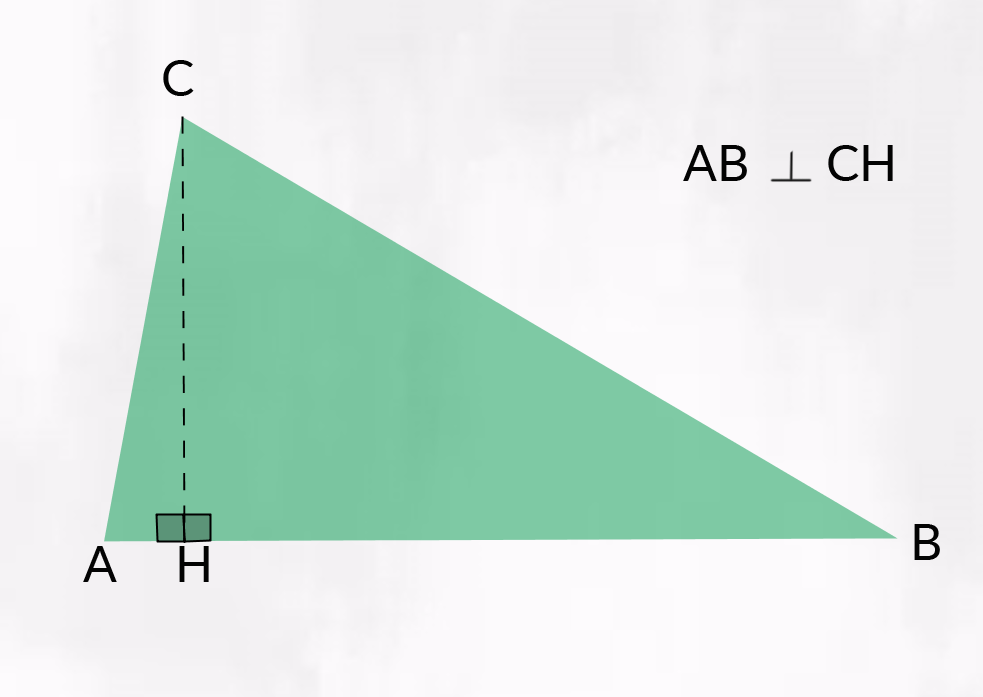
Diciamo che £$ CH $£ è l’altezza relativa al lato £$ AB $£.

Possiamo disegnare un’altezza da ognuno dei tre vertici di un triangolo. Quindi ogni triangolo ha tre altezze! Le altezze possono essere interne o esterne al triangolo. Per esempio un triangolo ottusangolo ha due altezze esterne.

Teorema: Le altezze di un triangolo o i loro prolungamenti si incontrano in un unico punto.

Per la dimostrazione sfruttiamo il teorema degli assi appena dimostrato. Lo applichiamo ad un triangolo che costruiamo tracciando tutte le parallele dei lati passanti per il vertice opposto del triangolo di partenza. I vertici del primo triangolo sono punti medi di quello costruito e così gli assi di quest’ultimo sono altezze del primo!

L’ortocentro è il punto di incontro delle altezze o dei loro prolungamenti.

• In un triangolo acutangolo le altezze sono tutte interne; anche l’ortocentro è interno.
• In un triangolo rettangolo le altezze relative ai cateti sono proprio i cateti. L’altezza relativa all’ipotenusa è interna al triangolo. L’ortocentro coincide con il vertice dell’angolo retto.
• In un triangolo ottusangolo due altezze sono esterne e una è interna. L’ortocentro è esterno al triangolo.

Mediane e baricentro

Il baricentro è il punto di equilibrio

Cos’è la mediana di un triangolo

La mediana di un triangolo rettangolo

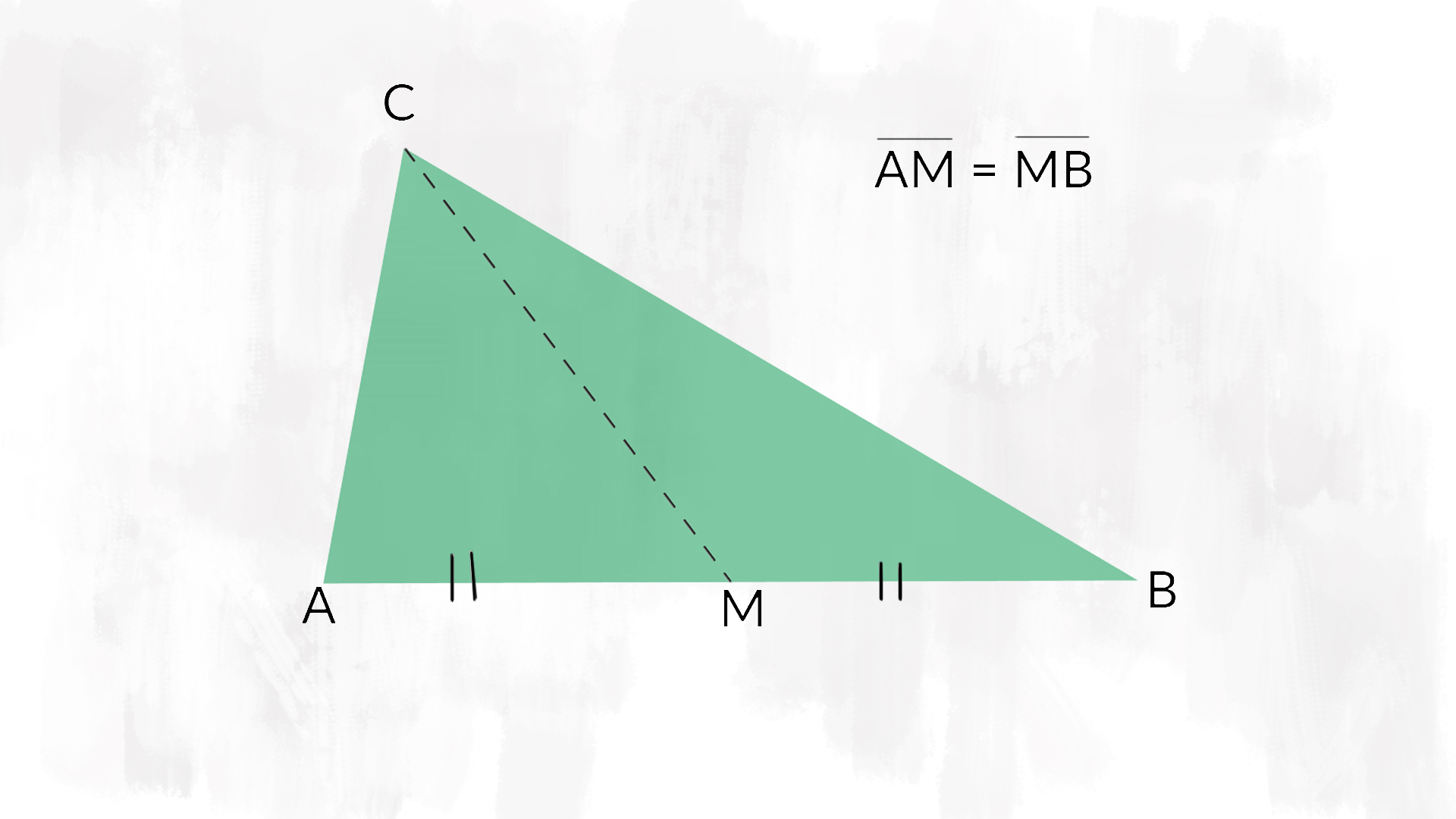
La parola mediana significa “che sta in mezzo”. Per disegnare una mediana di un triangolo, partiamo da un vertice e tracciamo il segmento che congiunge il vertice con il punto medio del lato opposto.
Nella figura, £$ M $£ è il punto medio del lato £$ AB $£. Diciamo che £$ CM $£ è la mediana relativa al lato £$ AB $£.

Possiamo disegnare una mediana da ognuno dei tre vertici di un triangolo. Quindi ogni triangolo ha tre mediane!
Le mediane sono sempre interne al triangolo.

Teorema: Le mediane di un triangolo si incontrano in un punto. Ogni mediana resta divisa dal baricentro in due parti e quella a cui appartiene il vertice del triangolo è il doppio dell’altra.

Disegniamo due mediane e dimostriamo la seconda parte del teorema applicando il teorema di Talete e le proprietà dei parallelogrammi. Per concludere dimostriamo che anche la terza mediana rispetta questa proprietà, e che passa per il punto di intersezione delle altre due mediane perché è l’unico punto che divide ogni segmento in due parti, una doppia dell’altra.

Il baricentro è il punto di incontro delle mediane di un triangolo.

In fisica, il baricentro è, sotto l’azione della gravità, il centro di massa. Il baricentro di un oggetto è il punto in cui possiamo immaginare concentrata tutta la sua massa. Un modo per determinare il baricentro di un oggetto è… appenderlo al muro.

Bisettrici e incentro

La bisettrice di un angolo è la semiretta che ha come origine il vertice dell’angolo e lo divide in due parti uguali.

Ogni triangolo ha tre angoli interni, quindi ha tre bisettrici, una per ciascun angolo.
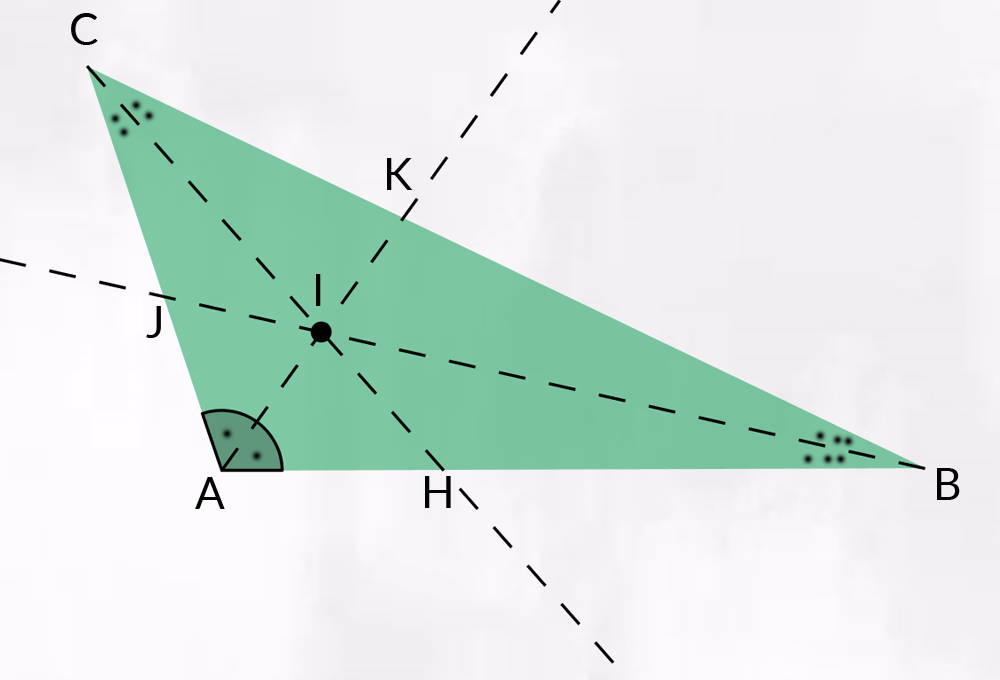
Nella figura, la semiretta di origine £$ C $£ che passa per £$ H $£ è la bisettrice dell’angolo £$ A\hat{C}B $£.

Le tre bisettrici di un triangolo si incontrano sempre in un unico punto chiamato incentro.
In ogni triangolo l’incentro è interno.

L’incentro ha una interessante proprietà: è equidistante dai tre lati del triangolo. Infatti l’incentro è il centro della circonferenza inscritta in un triangolo.
£$ \overline{IK} =\overline{IJ}=\overline{IH} $£

Incentro nel triangolo acutangolo

Incentro nel triangolo rettangolo

Incentro nel triangolo ottusangolo

Differenza tra incentro e excentro

Teorema: Le bisettrici degli angoli interni di un triangolo si incontrano in un unico punto.
Per dimostrare il teorema tracciamo prima due bisettrici del triangolo, ragioniamo sull’ampiezza degli angoli per capire che non possono essere parallele e quindi si incontrano in un punto. Per dimostrare che anche la terza bisettrice passa per quel punto tracciamo gli assi dei lati e ragioniamo sulle loro proprietà.

L’incentro è il centro della circonferenza inscritta, ovvero è il punto d’incontro delle bisettrici di un triangolo.

Corollario: Ogni triangolo è circoscrivibile a una circonferenza che ha come centro l’incentro del triangolo.

L’excentro è il punto di incontro delle bisettrici di due angoli esterni di un triangolo con la bisettrice dell’angolo interno non adiacente agli angoli.

Assi e circocentro

L’asse di un segmento è la retta perpendicolare al segmento passante per il suo punto medio.
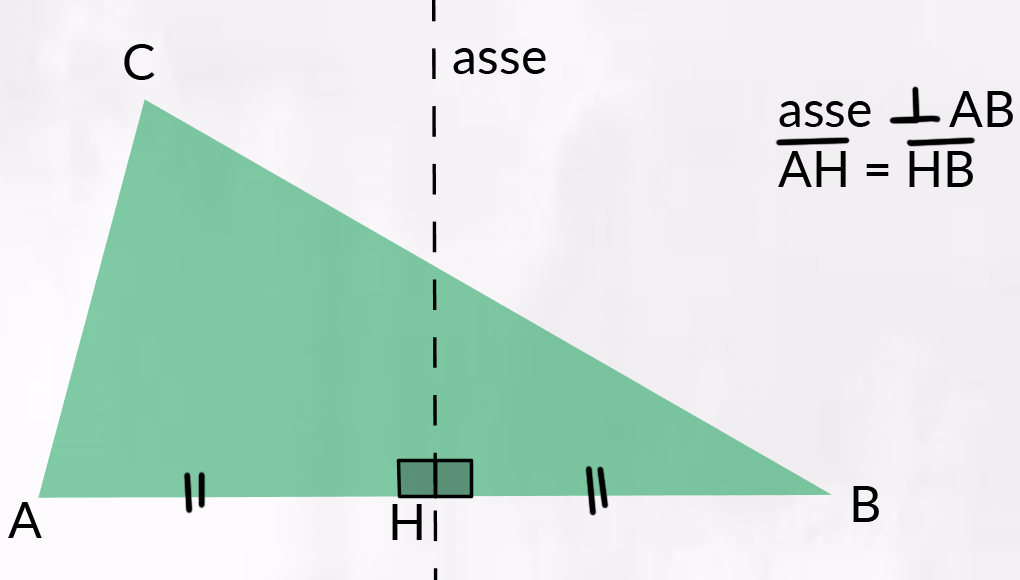
Gli assi di un triangolo sono gli assi dei lati del triangolo.

Nella figura, £$ H $£ è il punto medio del lato £$ AB $£ e la retta passante per £$ H $£ e perpendicolare al lato, è l’asse di £$ AB $£.

Possiamo disegnare un asse per ognuno dei tre lati di un triangolo. Quindi ogni triangolo ha tre assi!

Teorema: Gli assi dei lati di un triangolo si incontrano in un unico punto.
Per la dimostrazione applichiamo il teorema dell’esistenza di una circonferenza per tre punti e la definizione di asse del segmento.

Il circocentro è il centro della circonferenza circoscritta, ovvero il punto d’incontro degli assi dei lati di un triangolo.

I tre assi di un triangolo si incontrano sempre in un unico punto chiamato circocentro.

• In un triangolo acutangolo il circocentro è interno.
• In un triangolo rettangolo il circocentro coincide con il punto medio dell’ipotenusa.
• In un triangolo ottusangolo l’ortocentro è esterno al triangolo.

Il circocentro ha una interessante proprietà: è equidistante dai tre vertici del triangolo. Infatti il circocentro è il centro della circonferenza circoscritta al triangolo.

Circocentro nel triangolo acutangolo

Circocentro nel triangolo rettangolo

Circocentro nel triangolo ottusangolo

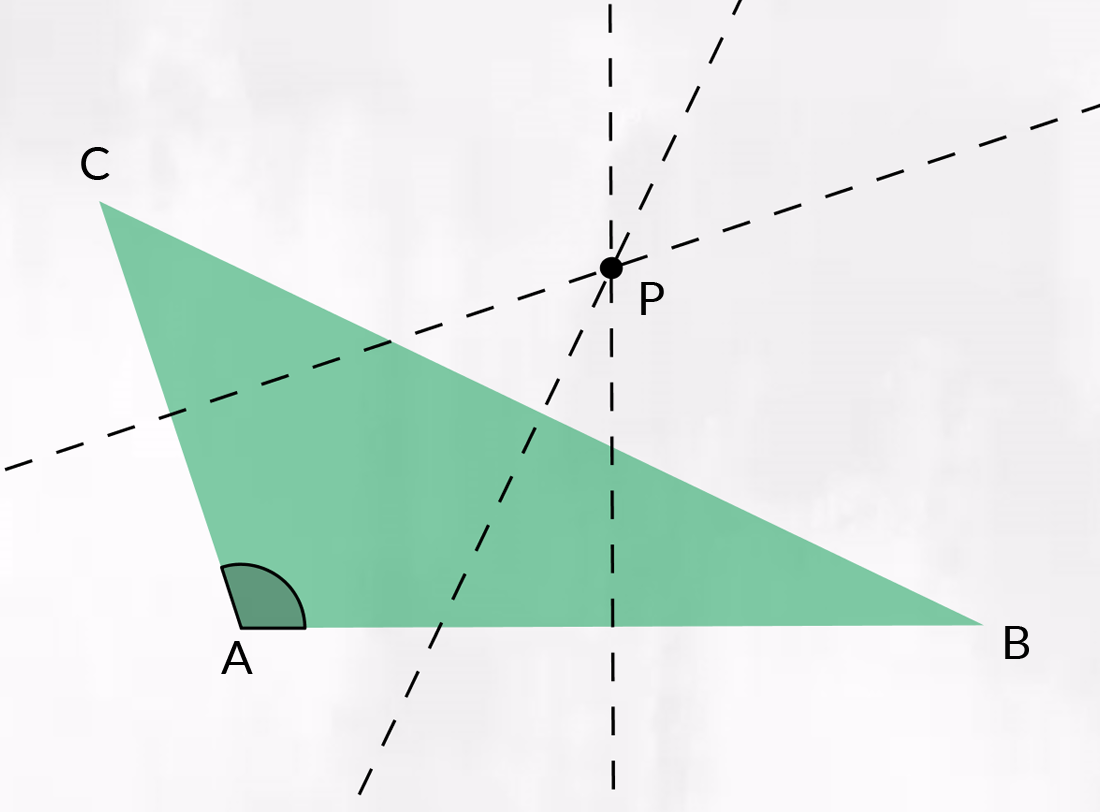
Casi particolari: il triangolo isoscele e il triangolo equilatero

I punti notevoli di un triangolo isoscele e di un triangolo equilatero hanno proprietà sorprendenti!

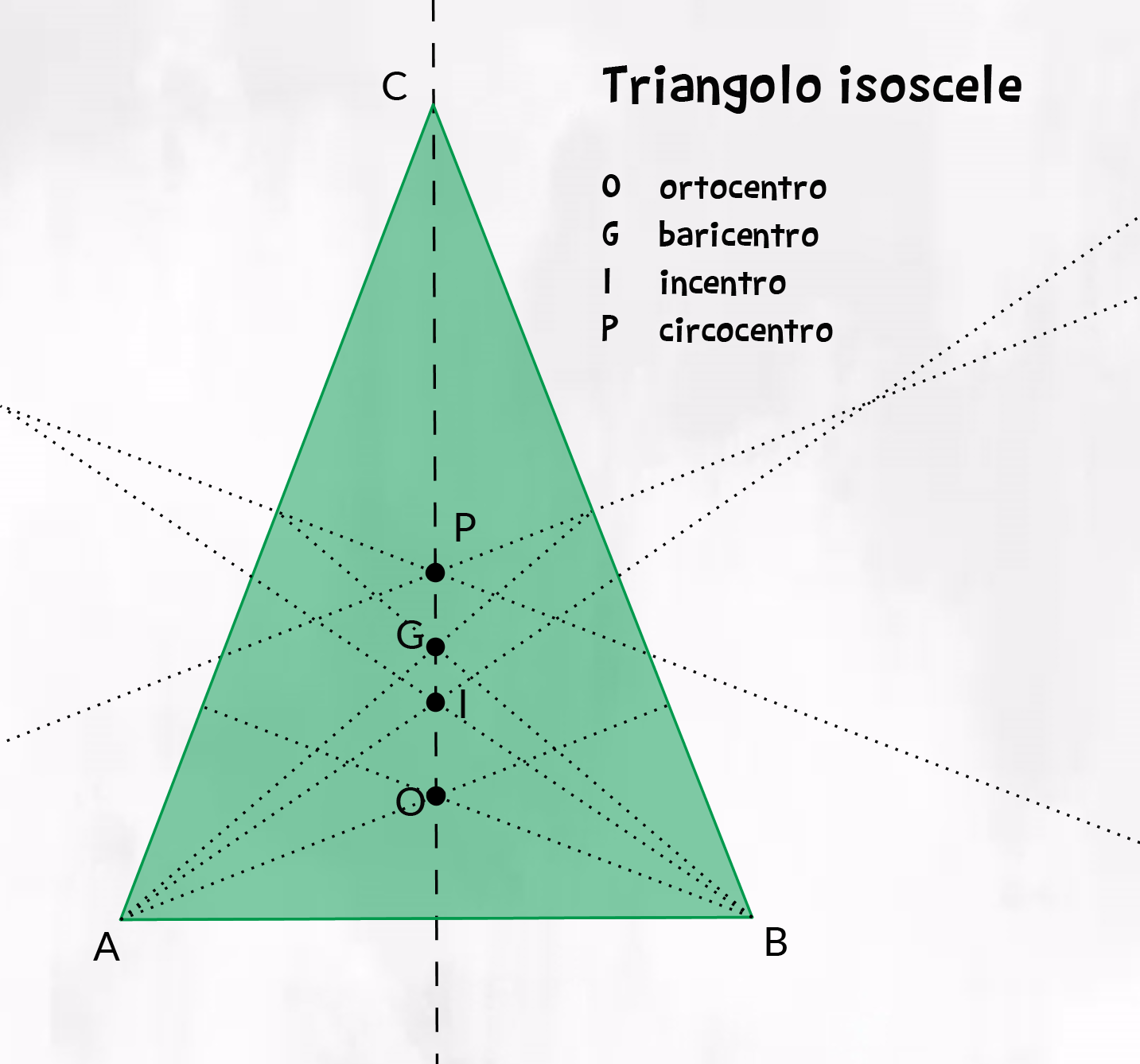
In un triangolo isoscele l’altezza, la mediana, la bisettrice e l’asse relative alla base coincidono!

Non vale lo stesso per le altezze, le mediane, le bisettrici e le assi relative ai lati obliqui: queste NON coincidono.
I punti notevoli di un triangolo isoscele appartengono tutti alla stessa retta, cioè ortocentro, baricentro, incentro e circocentro sono punti di una stessa retta, che è l’asse relativo alla base.

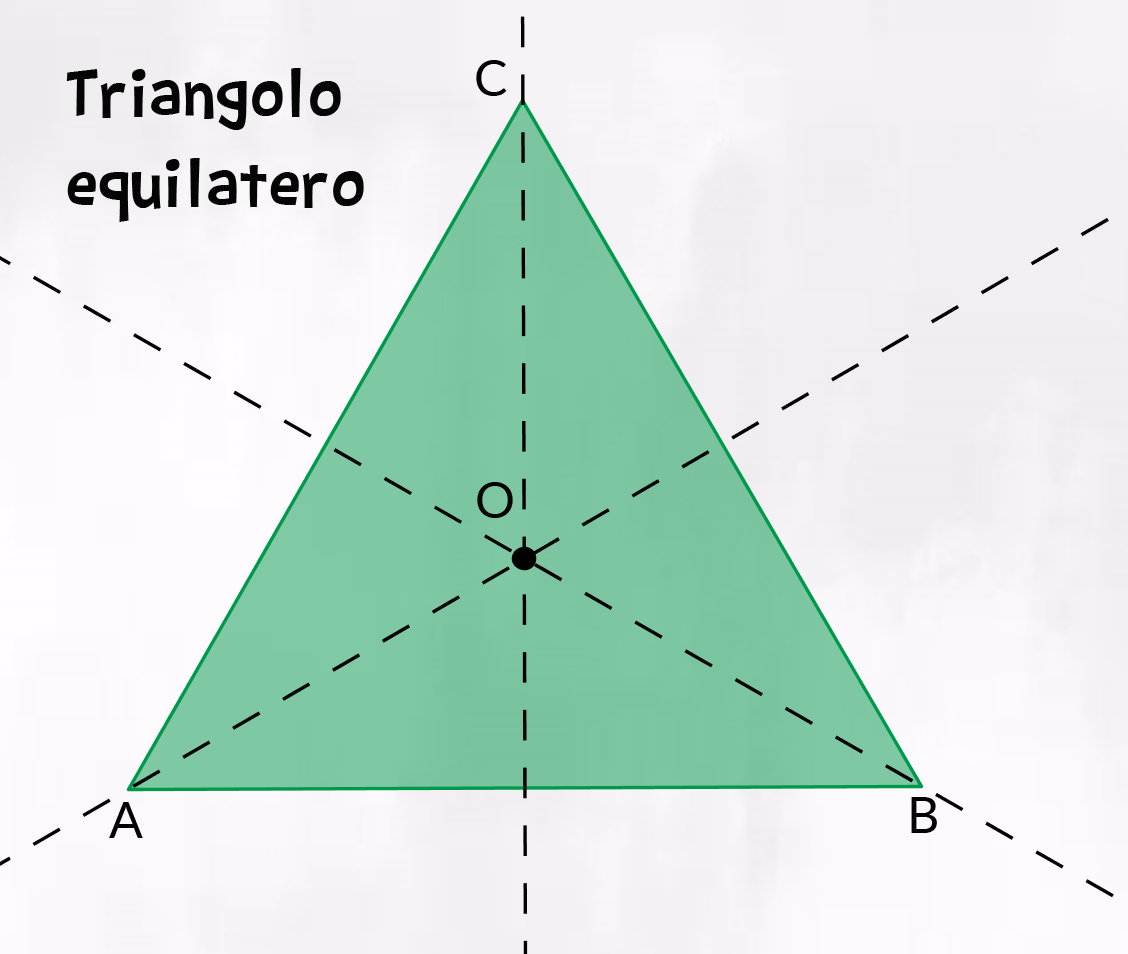
In un triangolo equilatero l’altezza, la mediana, la bisettrice e l’asse relativa a ciascun lato coincidono! Basta tracciare uno di questi elementi notevoli per individuare tutti gli altri.

Tutti i punti notevoli di un triangolo equilatero, quindi, coincidono! Ortocentro, baricentro, incentro e circocentro sono lo stesso punto!

Sfida sui punti notevoli di un triangolo

Sfida:

Soluzione:

Una torta con sopra disegnato un triangolo: quest’ultimo deve essere posizionato in modo tale che i suoi vertici siano tutti sulla circonferenza. Ma come capisci qual è il centro della torta? Risolvi la sfida sui punti notevoli di un triangolo e poi corri ad allenarti con gli esercizi!

Cosa potrebbero chiederti nell’interrogazione

Sai qual è la differenza tra incentro e baricentro? E che cos’è il circocentro? Mettiti alla prova rispondendo alle domande dell’interrogazione sui punti notevoli del triangolo che trovi in questo video!