La rappresentazione grafica dei dati statistici
La rappresentazione grafica dei dati statistici è un aspetto cruciale nell’analisi e nell’interpretazione delle informazioni in molti campi, dalla ricerca scientifica al business, dall’economia alla sociologia. Grafici come aerogrammi, istogrammi e diagrammi a barre offrono un mezzo visivo per comprendere e comunicare complessi insiemi di dati in modo chiaro ed efficace. In questo articolo, ci concentreremo sulla varietà di metodi grafici utilizzati per rappresentare i dati, esplorando come ogni tipo di grafico possa essere impiegato per evidenziare diversi aspetti dei dati.
Inizieremo con gli aerogrammi, che sono utili per mostrare proporzioni e relazioni in dati categorici, e discuteremo come la loro disposizione circolare fornisca una visione d’insieme intuitiva di intere distribuzioni. Successivamente, passeremo agli istogrammi, strumenti potenti per visualizzare la distribuzione di dati quantitativi, e vedremo come la loro capacità di mostrare frequenze all’interno di intervalli definiti aiuti a identificare pattern e tendenze.
Esamineremo i diagrammi a barre, che sono tra i grafici più versatili e comunemente usati. Questi diagrammi sono particolarmente efficaci nel confrontare quantità tra diverse categorie. Esploreremo sia i diagrammi a barre orizzontali che quelli verticali e discuteremo in che modo la scelta tra i due possa influenzare la leggibilità e l’interpretazione dei dati.
Infine, tratteremo altri formati di rappresentazione grafica, ognuno dei quali ha il proprio insieme unico di forze e applicazioni. Vediamoli insieme!
I diagrammi a barre
Ecco una tabella che raccoglie i chilometri percorsi da Andrea per andare in vacanza in estate negli ultimi £$5$£ anni.
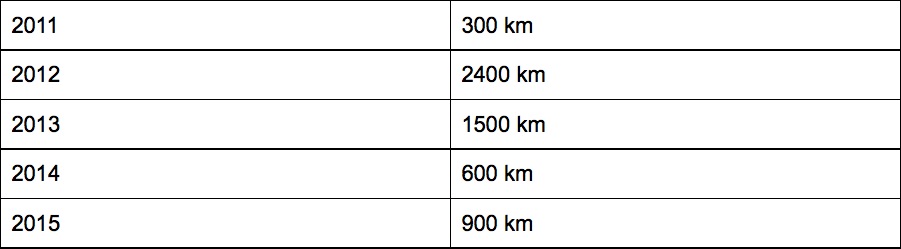
Per rappresentarla costruiamo un diagramma a barre.
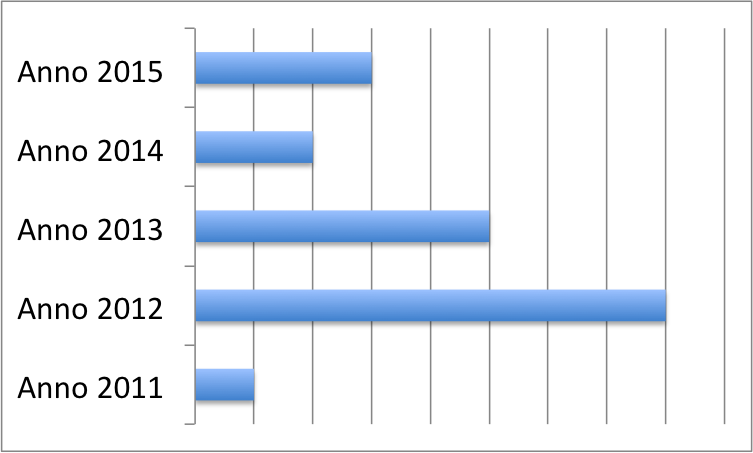
Ogni dato è rappresentato da un rettangolo.
Abbiamo scelto un’unità di misura: £$1$£ unità rappresenta £$300\text{ km}$£.
Infatti nel £$2012$£ Andrea ha percorso £$2400\text{ km}$£ e il rettangolo corrispondente è lungo 8 unità: £$8\cdot300\text{ km}=2400\text{ km}$£!
La lunghezza del rettangolo corrisponde al numero di chilometri percorsi. Devi sempre specificare qual è l’unità di misura del tuo diagramma!
Quanti chilometri ha percorso in totale Andrea negli ultimi £$3$£ anni per recarsi in vacanza d’estate? Possiamo sommare la lunghezza dei rettangoli degli ultimi £$3$£ anni £$(2015, 2014, 2013)$£, cioè £$5+2+3=10$£ unità che corrispondono a £$10\cdot300\text{ km}=3000\text{ km}$£!
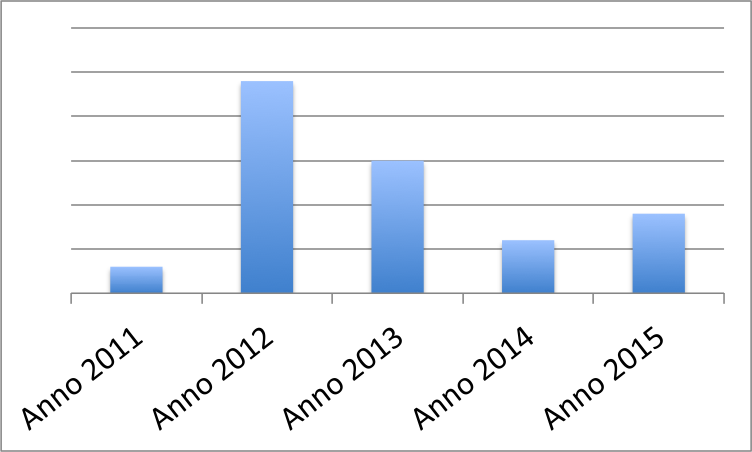
Puoi costruire un diagramma a barre anche con rettangolini “verticali”. Oppure puoi disporre i rettangolini attaccati l’uno all’altro, senza lasciare spazi vuoti: i diagrammi fatti in questo modo si chiamano istogrammi.
Gli areogrammi
Hai mai sentito parlare di un referendum? A volte quando in un paese è necessario prendere una decisione importante, i cittadini sono chiamati a esprimere la loro opinione con un voto. Sì può votare “Sì” o “No” ad una proposta.
Per esempio ecco i risultati di un referendum dove i cittadini hanno dovuto esprimere la loro opinione su due proposte, la Proposta 1 e la Proposta 2:
- £$\frac{1}{2}$£ dei cittadini ha detto “Sì” solo alla Proposta 1
- £$\frac{1}{8}$£ dei cittadini ha detto “Sì” a entrambe le proposte
- £$\frac{1}{8}$£ dei cittadini ha detto “Sì” solo alla Proposta 2
- tutti gli altri hanno detto “No” a entrambe.
Puoi rappresentare la situazione con un areogramma.
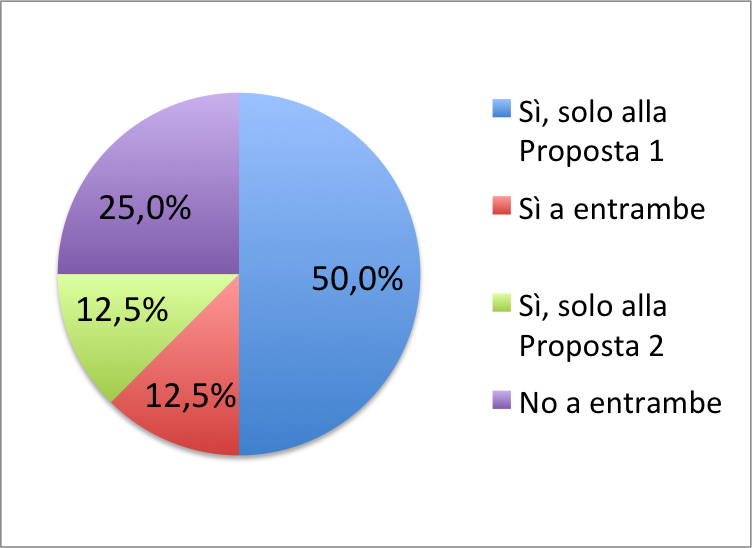
L’intera torta rappresenta il totale dei cittadini che hanno votato al referendum.
Ogni fetta colorata rappresenta una parte dei cittadini. La fetta più grande, che rappresenta la metà della torta, corrisponde ai cittadini che hanno votato “Sì” solo alla Proposta 1. Accanto alla torta trovi la legenda: è fondamentale per poter leggere il grafico! Dice a che cosa corrisponde il colore di ciascuna fetta.
Su un areogramma si rappresentano spesso i valori percentuali.
La torta intera è il £$1\text{ intero}=100\%=\frac{100}{100}$£.
La fetta azzurra è £$\frac{1}{2}$£ della torta: £$\frac{1}{2}=0,5=\frac{50}{100}$£. La percentuale corrispondente è £$\frac{50}{100}=50\%$£.
La fetta verde è £$\frac{1}{8}$£ della torta: £$\frac{1}{8}=0,125=\frac{12,5}{100}$£. La percentuale corrispondente è £$\frac{12,5}{100}=12,5\%$£.
Quanti cittadini hanno votato “No” a entrambe le proposte? La fetta viola della torta corrisponde a £$\frac{1}{4}$£ dell’intero. Un quarto dei cittadini hanno votato “No” ma non possiamo conoscere il numero esatto di cittadini: questa rappresentazione non ci dice nulla sui dati numerici.
Gli ideogrammi
A Margherita piace lo sport! Ama guardarlo ma anche praticarlo, come molti dei suoi compagni di scuola. Ma qual è lo sport più praticato tra i suoi amici? Per rispondere a questa domanda, decide di fare un sondaggio.
Alla fine della giornata tutti i suoi compagni hanno risposto e Margherita decide di organizzare tutti i
dati in una tabella speciale.
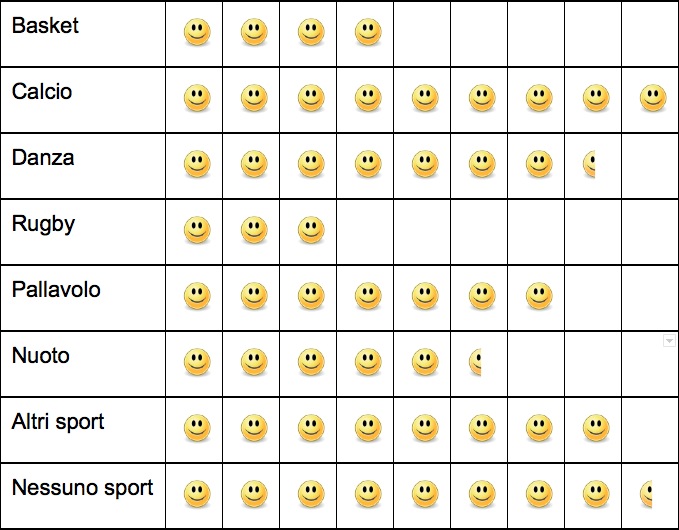
Per esempio, Margherita disegna £$3$£ simboli per il rugby, allora £$3\cdot2=6$£ studenti giocano a rugby.

chiave di lettura dell’ideogramma. Senza questa chiave di lettura non sarebbe possibile sapere quanti studenti praticano ciascuno sport e l’ideogramma sarebbe incompleto. Ricorda sempre di specificare qual è la chiave di lettura quando costruisci un ideogramma!
Quanti compagni sono troppo pigri e non praticano nessuno sport? Se 

Quanti sono i compagni di Margherita? Per rispondere a questa domanda, contiamo tutti i simboli che Margherita ha inserito nell’ideogramma. Ci sono £$51$£ simboli interi e £$3$£ mezzi simboli. Allora gli studenti della scuola sono £$51\cdot2+3\cdot1=102+3=105$£!
I diagrammi cartesiani
Paolo si sta allenando per la prossima gara di atletica. Come riscaldamento, comincia con 10 minuti di camminata veloce e 4 minuti di corsa. Il suo allenatore ha raccolto dei dati, misurando lo spazio percorso ogni 2 minuti.
Ecco la tabella dei dati raccolti:

L’allenatore costruisce un diagramma cartesiano.
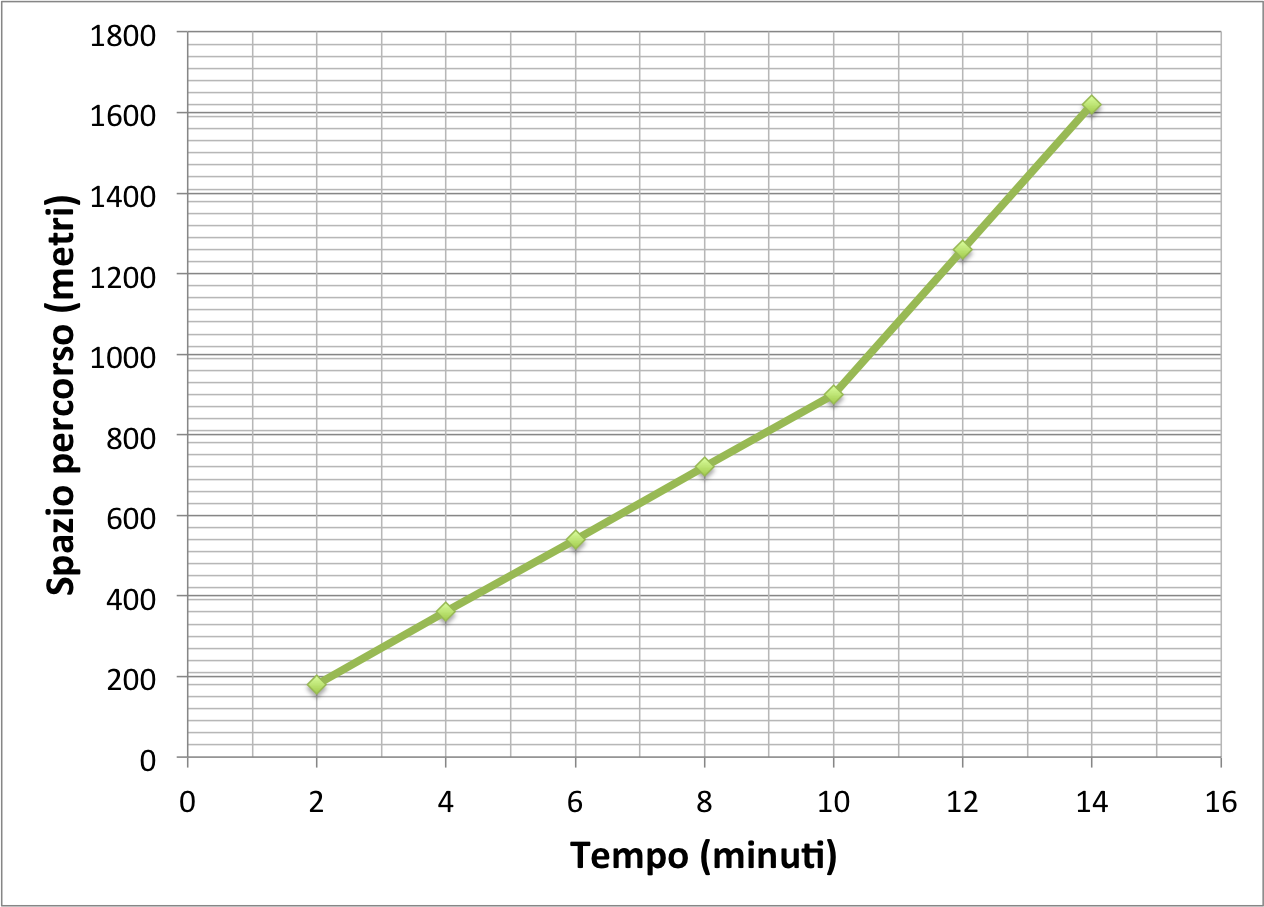
Sull’asse orizzontale segna il tempo misurato in minuti.
Sull’asse verticale segna lo spazio percorso misurato in metri.
Per ogni coppia di valori tempo e spazio segna un punto sul diagramma. Poi unisce i punti con una linea continua.
Quanti metri ha percorso Paolo dopo 7 minuti?
Sull’asse orizzontale cerchiamo il valore 7 minuti. Tracciamo una linea verticale fino a incontrare la linea verde del grafico. Poi tracciamo una linea orizzontale fino a incontrare l’asse verticale dello spazio. Possiamo seguire le linee della griglia!
Troviamo un valore poco superiore a 600 metri.
Dopo 7 minuti di riscaldamento, Paolo ha percorso poco più di 600 metri.
