Legge di Torricelli e la pressione dei fluidi
La fisica è una scienza che si nutre di leggi fondamentali, principi universali che ci permettono di interpretare e prevedere il comportamento del mondo che ci circonda. Tra queste, la legge di Torricelli occupa un posto di rilievo. Protagonista di innumerevoli esperimenti scolastici e applicata in molteplici ambiti scientifici e ingegneristici, questa legge riveste un’importanza che non può essere sottovalutata.
Evangelista Torricelli, fisico e matematico italiano del XVII secolo, è famoso per la sua legge sulla velocità di un fluido che esce da un orifizio. Tale legge prende il suo nome ed è un concetto chiave nell’ambito dell’idrodinamica. Ma perché la legge di Torricelli è così importante? Perché è essenziale per capire i principi di base dell’ingegneria dei fluidi e ha una vasta gamma di applicazioni, dalla fisica alla chimica, dalla biologia all’ingegneria. È alla base dei calcoli che riguardano dighe e serbatoi, ci aiuta a comprendere come funzionano gli iniettori dei motori a reazione, e ci permette di progettare sistemi di irrigazione efficienti.
Scopriamola insieme!
- Enunciato della legge di Torricelli
- L'esperimento di Torricelli
- Legge di Torricelli e Teorema di Bernoulli
- Legge di Torricelli: un esperimento pratico
Enunciato della legge di Torricelli

La legge di Torricelli afferma che è possibile calcolare la velocità posseduta da un fluido che scorre abbandonando un serbatoio e passando attraverso una sezione sufficientemente piccola (se confrontata con le dimensioni del serbatoio stesso). L’espressione indicante tale valore sarà la seguente:
£$V=\sqrt{2*g*h}$£
Dove:
£$V$£ è la velocità del fluido, espressa in £$[\frac{m}{s}]$£
£$g$£ è l’accelerazione di gravità, uguale a £$9.81 [\frac{m}{s^{2}}]$£
£$h$£ è la profondità a cui si trova il foro dal quale fuoriesce il fluido, misurata a partire dal pelo libero ed espressa in metri, £$[m]$£
L’esperimento di Torricelli
L’esperimento che ha condotto alla formulazione della legge di Torricelli ha una grande importanza non solo per i risultati ottenuti, ma anche per l’approccio scientifico che ha introdotto, basato sull’osservazione accurata e sulla deduzione.
L’esperimento di Torricelli si svolse nel 1643. L’obiettivo era quello di dimostrare che l’aria ha peso e che è la pressione atmosferica, e non un vuoto come si riteneva fino ad allora, a mantenere l’acqua in un tubo capovolto. Torricelli prese un tubo di vetro lungo un metro, lo riempì completamente d’acqua e lo chiuse con un dito. Poi immerse il capo aperto del tubo in una vasca d’acqua e rimosse il dito. Notò che una parte dell’acqua scendeva nel tubo fino a raggiungere una certa altezza, che si manteneva costante.
Torricelli attribuì questo fenomeno alla pressione atmosferica. L’aria esercita una pressione su ogni superficie con cui viene a contatto, inclusa quella dell’acqua nella vasca. Questa pressione è sufficiente a sostenere l’acqua nel tubo fino a una certa altezza. Al di sopra di questa altezza, la pressione dell’acqua nel tubo supera quella dell’aria all’esterno, e l’acqua scende fino a quando le due pressioni si bilanciano.
Questo esperimento fu solo l’anticipazione della scoperta della legge di Torricelli. L’osservazione che la velocità di un fluido che esce da un orifizio dipende dalla sua altezza nel recipiente è diretta conseguenza dell’osservazione che la pressione di un fluido aumenta con la profondità. Questo fenomeno, noto come principio di Pascal, è la base dell’idrostatica, e la legge di Torricelli ne è una diretta applicazione nell’ambito dell’idrodinamica.
In conclusione, l’esperimento di Torricelli è un esempio lampante di come l’osservazione sperimentale e l’analisi teorica si combinino per produrre progressi nella comprensione scientifica. Ancora oggi, questo esperimento è riproposto nei laboratori scolastici e universitari come introduzione alle leggi dei fluidi e alla metodologia scientifica.
Legge di Torricelli e Teorema di Bernoulli
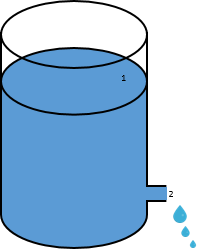
La legge di Torricelli può essere ricavata a partire dalla formulazione del teorema di Bernoulli. Proviamo ad indicare con il pedice £$1$£ il pelo libero del serbatoio e con il pedice £$2$£ la sezione di uscita del fluido. Il teorema di Bernoulli può essere scritto per confrontare il fluido in questi due punti:
£$p_{1} + \frac{1}{2} \cdot \varrho \cdot V_{1}^{2}+\varrho \cdot g \cdot h_{1} = $£ £$ p_{2} + \frac{1}{2} \cdot \varrho \cdot V_{2}^{2}+\varrho \cdot g \cdot h_{2}$£
Qualche semplificazione può poi essere fatta considerando che:
- in corrispondenza del pelo libero del serbatoio l’acqua ha velocità nulla (l’ipotesi che il serbatoio sia sufficientemente grande serve proprio a poter immaginare che il livello dell’acqua al suo interno non scenda tanto velocemente da poter apprezzare una vera e propria velocità sul pelo libero): £$V_{1}=0$£.
- la pressione sul pelo libero dell’acqua, così come in corrispondenza della sezione di uscita corrisponderà al valore atmosferico; i due termini possono quindi essere semplificati: £$p_{1}=p_{2}=p_{atm}$£.
- la differenza di quota esistente tra i due punti indicati può essere per semplicità indicata con la generica lettera £$h$£: £$h_{1}-h_{2}=h$£.
Di conseguenza, è possibile scrivere:
£$\varrho \cdot g \cdot (h_{1}-h_{2}) = \frac{1}{2} \cdot \varrho \cdot V_{2}^{2}$£ £$\varrho \cdot g \cdot h = \frac{1}{2} \cdot \varrho \cdot V_{2}^{2}$£
Da cui, si può ricavare:
£$V_{2}^{2}=\frac{2 \cdot \varrho \cdot g \cdot h}{\varrho}$£ £$V_{2}=\sqrt{2 \cdot g \cdot h}$£
Legge di Torricelli: un esperimento pratico
Nella lezione legge di Stevino si è visto come tramite un semplice esperimento sia possibile osservare il diverso comportamento di un getto di acqua che fuoriesce da una bottiglietta a seconda della posizione del foro lungo l’altezza della stessa. La diversa quota raggiunta dall’acqua può essere spiegata grazie alla legge di Stevino. Ora, grazie all’utilizzo della legge di Torricelli possiamo direttamente spiegarci la diversa velocità raggiunta dai tre getti. La legge di Torricelli afferma infatti che la velocità del fluido in uscita può essere così ricavata:
£$V_{2}=\sqrt{2*g*h}$£
Siccome con £$h$£ indichiamo la diversa profondità del foro rispetto al pelo libero, possiamo facilmente renderci conto di come ad una profondità maggiore del foro corrisponderà una più alta velocità del flusso che sta fuoriuscendo dalla bottiglietta.
