Il Sistema Internazionale: grandezze e unità di misura
Quando si parla di misure, sia che si tratti di lunghezza, massa, tempo o qualsiasi altra grandezza fisica, è fondamentale avere un sistema di riferimento standard e universalmente accettato. Questo è esattamente ciò che il Sistema Internazionale, spesso abbreviato in SI, offre. Si tratta di un insieme standardizzato di unità di misura utilizzato in tutto il mondo per garantire che, quando parliamo di un determinato valore o misura, tutti possano comprenderlo nello stesso modo, indipendentemente dalla lingua o dal paese di origine.
Il Sistema Internazionale non è solo una convenzione arbitraria, ma piuttosto il risultato di anni di ricerca e collaborazione internazionale, al fine di stabilire un insieme di unità di misura che rispecchiano la realtà fisica in modo accurato e riproducibile. Ad esempio, quando parliamo di un metro nel SI, ci riferiamo a una lunghezza specifica che ha la stessa valore ovunque nel mondo.
L’adozione di un sistema uniforme come il SI ha enormi vantaggi, specialmente in ambito scientifico e tecnologico; assicura che le ricerche condotte in differenti parti del mondo siano compatibili tra loro e che le innovazioni tecnologiche possano essere implementate e comprese su scala globale. Scopriamolo insieme!
- Perché abbiamo bisogno delle unità di misura
- Quando nasce il Sistema Internazionale
- Le unità di misura base del Sistema Internazionale
- A cosa servono le unità di misura del Sistema Internazionale
- Grandezze derivate e grandezze fondamentali nel S.I.
Perché abbiamo bisogno delle unità di misura
È importante per gli uomini utilizzare le stesse unità di misura, sia per ottenere più ordine nel mondo, sia per evitare equivoci.
Il 23 settembre 1999, per esempio, la sonda spaziale Mars Climate Orbiter sarebbe dovuta entrare nell’orbita di Marte ad una quota superiore a £$80 \text{ km}$£, in modo da evitare danni. Invece entrò in orbita a £$57 \text{ km}$£ dalla superficie distruggendosi completamente a causa dell’impatto con l’atmosfera.
Questo perché un software a Terra ragionava con unità di misura americane (libbra-forza per secondo) mentre la NASA ragionava con le unità di misura del Sistema Internazionale. Gli Stati Uniti d’America, infatti, sono uno dei pochi paesi al mondo in cui questo sistema, nato in Francia, non è accettato come unico sistema di misura.
Quando nasce il Sistema Internazionale
La prima standardizzazione di un sistema comune di pesi e misure avviene con la Rivoluzione Francese anche se, anche la monarchia francese era a favore di una risistemazione delle unità di misura per ragioni di commercio e controllo del territorio.
La Rivoluzione Francese avrebbe voluto spingersi ben oltre la “metricazione” dei pesi e delle misure e aspirava alla decimalizzazione del tempo. Il tempo decimale, ossia il giorno diviso in dieci ore divise in dieci minuti ciascuna, però, non sarà mai accettato. Le misure standard servono “Per tutti gli uomini” diceva il filosofo Condorcet, e possibilmente “per tutto il tempo”.
La Francia nel XVIII secolo stabilì alcune misure di base, come il metro. Nella seconda metà del 1800 molte nazioni aderirono alla proposta della Francia e cominciarono ad utilizzare il suo sistema, che a quel punto diventò internazionale.
Le unità di misura base del Sistema Internazionale
Il Sistema Internazionale (SI) delle unità di misura è oggi l’alfabeto che garantisce la coerenza interna e la possibilità di comunicare di replicare le misure fisiche. Il SI è stato modificato e ricostruito nei secoli.
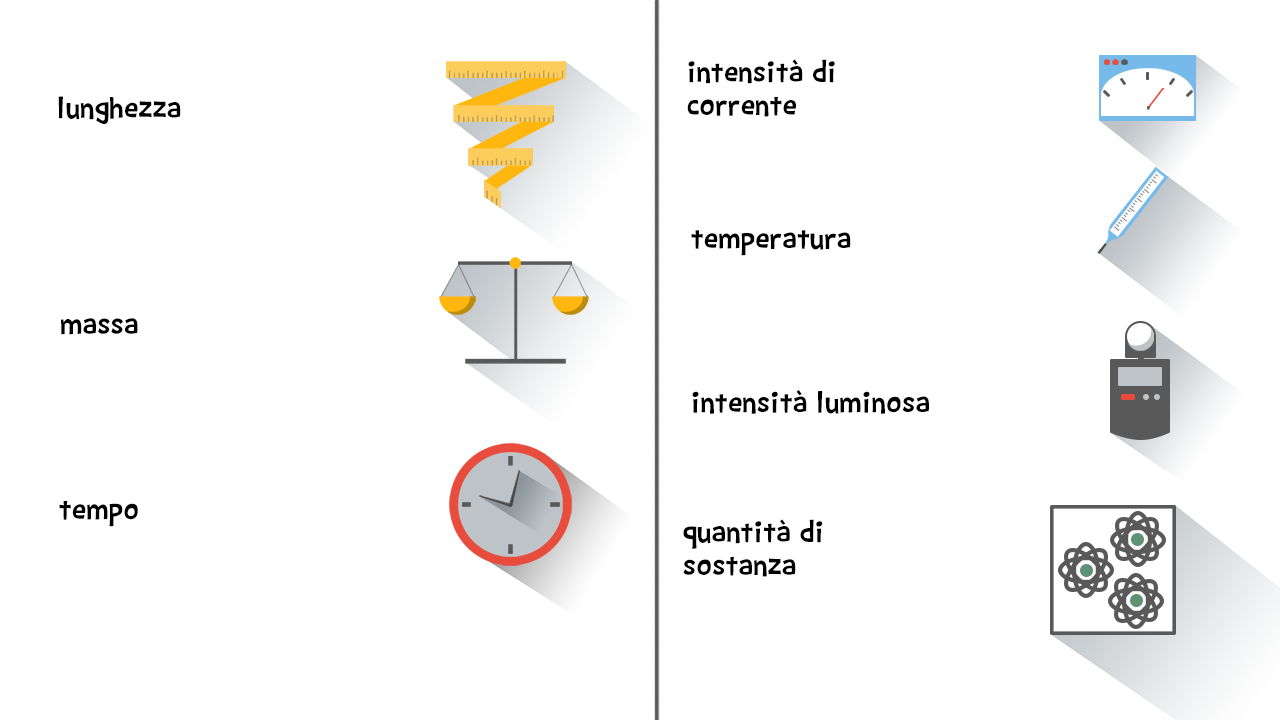
La sua attuale struttura si basa sulla definizione di sette unità fondamentali:
- il metro (£$\text{m}$£), unità di misura della lunghezza;
- il chilogrammo (£$\text{kg}$£), unità di misura della massa;
- il secondo (£$\text{s}$£), unità di misura dell’intervallo di tempo;
- l’ampere (£$\text{A}$£), unità di misura dell’ intensità di corrente elettrica;
- la mole (£$\text{mol}$£), unità di misura della quantità di sostanza;
- la candela (£$\text{cd}$£), unità di misura dell‘intensità luminosa;
- il kelvin (£$\text{K}$£) unità di misura della temperatura termodinamica.
Da queste unità di base possono essere derivate tutte le altre unità di misura della fisica.
Le definizioni delle unità di misura sono spesso molto complesse, ma permettono la massima precisione di calcolo.
Il £$\text{kg}$£ aveva una definizione semplice, ossia “è la massa del prototipo standard internazionale conservato a Sèvres (colui che creò il modello del kilogrammo con una lega di platino e iridio)”.
Il 20 maggio 2019 si è passati da una definizione di chilogrammo basata su un campione fisico (la massa del prototipo standard internazionale, un cilindro di platino e iridio, conservato a Sèvres) ad una definizione basata su una costante fisica. Il chilogrammo è la massa controbilanciata da una certa quantità di corrente e la costante che entra in gioco è quella di Planck.
Il £$\text{m}$£, invece, fu definito osservando la natura: è “la distanza percorsa dalla luce, nel vuoto, in £$\frac{1}{299792458}$£ di secondo”.
A cosa servono le unità di misura del Sistema Internazionale
L’unità di misura conferisce la dimensione a un dato fisico che, senza dimensione e senza unità di misura, è inutilizzabile. Un dato è composto da un numero, che viene misurato dagli strumenti, e dalla dimensione di quel numero, legata alla grandezza fisica che si sta misurando e che gli viene associata con l’unità di misura.
Essa è indicata da un simbolo, che contraddistingue la grandezza a cui si riferisce il numero.
Grandezze derivate e grandezze fondamentali nel S.I.
Abbiamo parlato delle grandezze fondamentali, cioè le sette grandezze principali secondo il Sistema Internazionale delle unità di misura.
Ora invece parleremo delle grandezze che derivano da queste sette!
Ciascuna di queste grandezze, infatti, utilizza unità di misura derivate da quelle fondamentali.
Facciamo qualche esempio.
L’area di una superficie ha come unità di misura il metro quadrato, ovvero £$\ m^2 $£ e dimensionalmente £$\ [L] [L] $£.
Il volume ha come unità di misura il metro cubo, ovvero £$\ m^3 $£ e dimensionalmente £$\ [L] [L] [L] $£.
La velocità (£$\vec v$£) è il rapporto tra lo spazio percorso e il tempo impiegato a percorrerlo: £$ v = \frac{s}{t}$£.
Dal punto di vista delle dimensioni, la velocità è, quindi, £$\dfrac{[L]}{[T]}$£, una lunghezza diviso un tempo. L’unità di misura è quella connessa alle due dimensioni, ossia £$\frac{m}{s}$£ (metri al secondo).
L’accelerazione è la variazione di velocità per il tempo: £$a= \dfrac{v}{t}$£. Dimensionalmente sarà, quindi £$\dfrac{[L]}{[T][T]}$£ e la sua unità di misura £$\dfrac{m}{s^2}$£.
Stesso discorso si estende, inalterato, a unità di misure più complesse.
La seconda legge della dinamica recita che la Forza £$(F)$£ è uguale a massa per accelerazione: £$F = m·a$£. La massa dimensionalmente è £$[M]$£, l’accelerazione dimensionalmente è £$\dfrac{[L]}{[T^2]}$£. Un Newton £$(1 N)$£, unità di misura della forza, sarà quindi £$\dfrac{(1 m ·1 kg)}{1 s^2}$£.
