Il modello del corpo nero e il suo spettro
Il corpo nero è un modello di un oggetto che può assorbire completamente le onde elettromagnetiche di qualsiasi lunghezza d’onda che lo colpiscono e, idealmente, riemetterle.
Un esempio di corpo nero si ha quando, in una giornata di sole, da fuori vediamo le finestre di un palazzo scure; questo perchè la stanza all’interno assorbe le radiazioni elettromagnetiche e non le riemette, comportandosi da corpo nero.
In laboratorio un corpo nero è formato da un oggetto cavo con un piccolo foro, mantenuto a temperatura costante e uniforme. Analizzando le emissioni di onde elettromagnetiche che fuoriuscivano dal foro, i fisici notarono che la lunghezza d’onda dipendeva solo dalla temperatura dell’oggetto e non dal materiale o dalle dimensioni del foro.
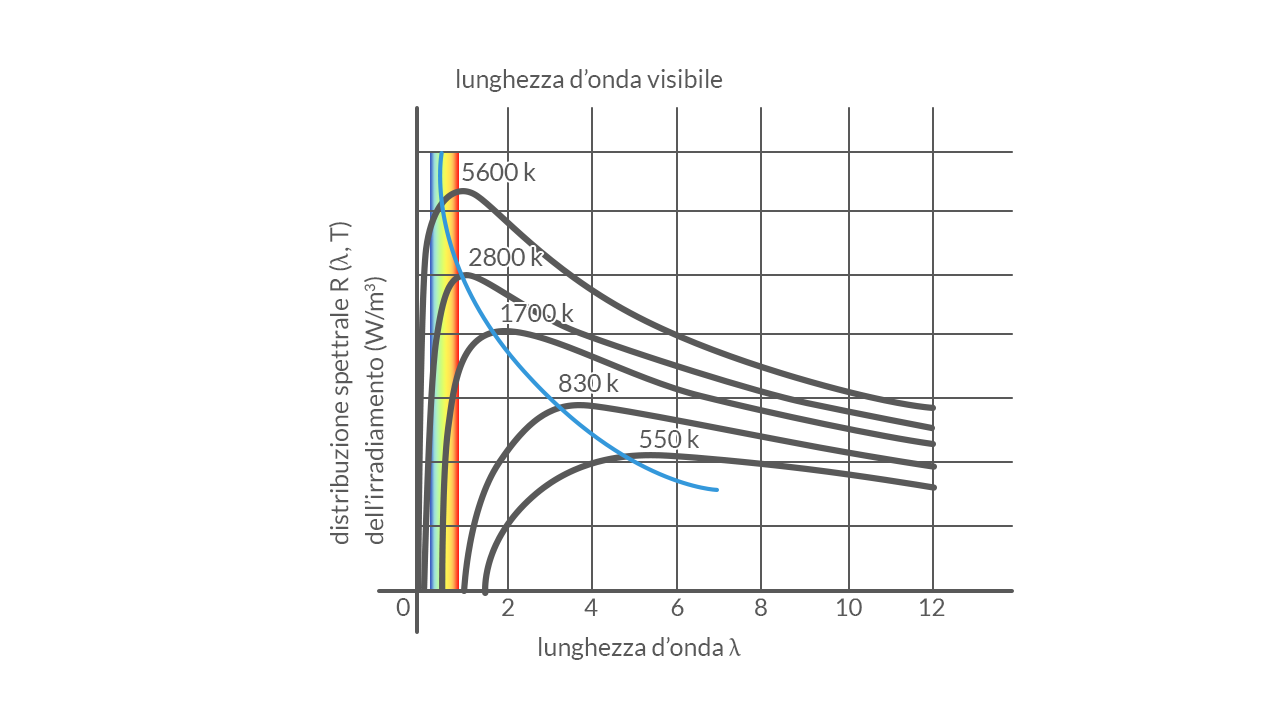
Gli esperimenti e i dati ottenuti avevano permesso di realizzare un grafico lunghezza d’onda-distribuzione spettrale dell’irradiamento del corpo nero che evidenziava la dipendenza della lunghezza d’onda unicamente dalla temperatura.
La distribuzione spettrale di una certa lunghezza d’onda £$\lambda$£ è la potenza che fuoriesce dal foro sotto forma di onde elettromagnetiche divisa per l’area £$A$£ del foro e per l’intorno £$\Delta \lambda$£ di £$\lambda$£: £$ R(\lambda , T)= \frac {P(\lambda , T)}{A\Delta \lambda}$£.
Si notava che al crescere della temperatura £$T$£ in Kelvin, la lunghezza d’onda £$\lambda_{max}$£ che corrisponde al massimo della funzione £$R(\lambda , T)$£, tendeva a valori sempre più piccoli secondo la legge sperimentale detta legge di spostamento di Wien: £$\lambda_{max}= \frac {2,90 \cdot 10^{-3} \ m \cdot K}{T}$£.
Notiamo che £$\lambda_{max}$£ dipende SOLO dalla temperatura £$T$£ del corpo e da nessun'altra grandezza.
