Formulario di fisica: i condensatori
La fisica moderna non si basa solo su particelle subatomiche o forze gravitazionali misteriose: alcuni dei suoi concetti più affascinanti emergono dalla teoria e dalle applicazioni dei componenti elettronici, come i condensatori. Questi dispositivi, sebbene sembrino banali a prima vista, giocano un ruolo cruciale nella tecnologia elettronica di oggi, dalla conservazione dell’energia in un flash fotografico all’avvio dei motori elettrici nelle automobili.
Le sfumature e la complessità dei condensatori risiedono nel loro funzionamento e nelle formule matematiche che ne descrivono le proprietà e le performance. Come possono questi piccoli dispositivi accumulare energia e rilasciarla quando necessario? Quali sono le formule chiave che ne guidano il comportamento?
Un condensatore è un dispositivo elettronico passivo utilizzato per immagazzinare energia in un campo elettrico. È costituito da due piastre conduttive separate da un isolante chiamato dielettrico. Quando una differenza di potenziale, o tensione, viene applicata alle piastre, si accumula una carica elettrica su di esse. Questa capacità di immagazzinare carica e, quindi, energia, rende il condensatore uno strumento essenziale in molte applicazioni elettroniche.
- Campo elettrico di un condensatore
- Capacità di un condensatore piano
- Definizione di condensatore
- Densità di energia di un condensatore
- Differenza di potenziale di un condensatore piano
- Energia potenziale di un condensatore
- Condensatori in parallelo
- Condensatori in serie
Campo elettrico di un condensatore
L’intensità del campo elettrico di un condensatore piano è: $$E=\frac{\sigma}{\epsilon_0}$$ dove con £$\sigma$£ si indica la densità superficiale di carica.
All’interno del condensatore il campo elettrico è uniforme e costante, mentre all’esterno è nullo. Se le armature hanno dimensioni finite, in prossimità delle estremità il campo elettrico non è più uniforme, le linee di forza si curvano a causa degli effetti di bordo.
Capacità di un condensatore piano
La capacità di un condensatore piano, le cui armature hanno area £$S$£ e sono poste a distanza £$d$£ nel vuoto, è: $$C= \frac{\epsilon_0 S}{d}$$
Se lo spazio tra le armature è riempito da un materiale dielettrico di costante dielettrica relativa £$\epsilon_r$£, la sua capacità aumenta e diventa pari a: $$C=\frac{\epsilon_0 \epsilon_r S}{d}$$
Tra le armature del condensatore il campo elettrico è uniforme e il suo modulo vale: $$E=\frac{\sigma}{\epsilon_0}$$ dove £$\sigma$£ è la densità superficiale di carica (in valore assoluto).
Definizione di condensatore
Un condensatore è un dispositivo costituito da due armature, una caricata con una carica £$+Q$£ e una con una carica £$-Q$£.
In particolare consideriamo i condensatori piani, ovvero quelli costituiti da due lastre piane parallele ed infinitamente estese, poste a distanza £$d$£ una dall’altra.
Densità di energia di un condensatore
La densità di energia nel volume occupato dal condensatore è: $$w_e=\frac{U}{Sd}$$
dove £$U=\frac{1}{2} \epsilon_0 SdE^2$£ e quindi: $$w_e= \frac{1}{2} \epsilon_0 E^2$$
Questa espressione della densità di energia del campo elettrico è generale e vale anche per campi variabili.
Differenza di potenziale di un condensatore piano
a differenza di potenziale tra due punti £$ A$£ e £$B$£ all’interno di un condensatore piano, dove il campo elettrico è uniforme, è calcolata con l’integrale espresso nel paragrafo 2.16:
$$V_B-V_A= E(y_A-y_B)$$
In particolare la differenza di potenziale tra le due armature di un condensatore piano è data da:
$$ \Delta V = E \cdot d $$
Energia potenziale di un condensatore
L’energia potenziale elettrica di un condensatore è:
$$U= \frac{1}{2} Q\Delta V= \frac{1}{2} C (\Delta V)^2 $$
ed è pari al lavoro richiesto per caricare le armature. Poiché tra le armature del condensatore c’è un campo elettrico che è nullo quando il condensatore è scarico e vale £$\dfrac{\sigma}{\epsilon_0}$£ quando sulle armature si è accumulata la carica £$Q$£, l’energia viene immagazzinata dal campo stesso.
I sistemi di condensatori in serie e in parallelo
I condensatori sono componenti elettronici che hanno la capacità di immagazzinare energia sotto forma di campo elettrico. La modalità con cui vengono collegati in un circuito determina non solo la capacità totale, ma anche come questa energia viene accumulata e rilasciata. Possono essere:
- In serie: quando si collegano condensatori in serie, si allineano uno dopo l’altro in una sequenza. Questo significa che la carica deve passare attraverso ogni condensatore uno alla volta. Poiché la carica non può dividersi tra condensatori in serie, tutti hanno la stessa carica. La configurazione in serie porta ad una capacità totale ridotta. Questo può essere utile quando si vuole limitare la capacità complessiva o si desidera una tensione di breakdown più elevata.
- In parallelo: in una configurazione parallela, i terminali di ogni condensatore sono collegati direttamente alla sorgente di alimentazione. Questo permette a ciascun condensatore di caricarsi indipendentemente dagli altri. Di conseguenza, la capacità totale in un sistema parallelo è la somma delle capacità dei singoli condensatori. I sistemi in parallelo sono utilizzati quando si necessita di una capacità elevata, come nell’avviamento di motori o nella filtrazione in alimentatori.
In molti dispositivi elettronici moderni, le combinazioni di condensatori in serie e in parallelo sono utilizzate per ottenere le specifiche desiderate. La comprensione delle differenze tra queste due configurazioni è fondamentale per chi si occupa di elettronica, sia a livello amatoriale che professionale.
Condensatori in parallelo
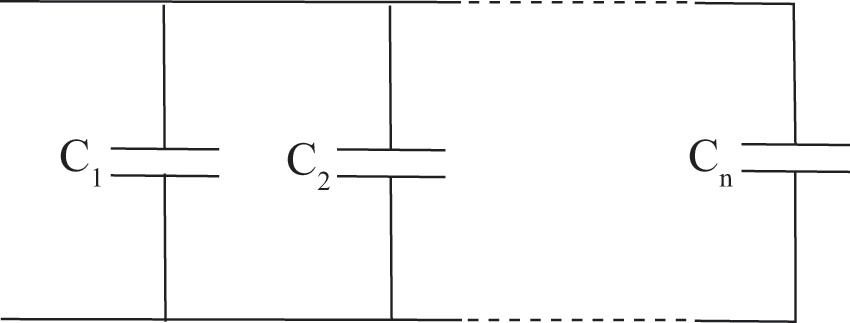
Le armature di ogni condensatore hanno la stessa d.d.p.,
la capacità equivalente è £$C_{eq}=\sum_{(i=1)}^n C_i$£.
Condensatori in serie

Le armature di ogni condensatore accumulano la stessa carica, la capacità equivalente è £$\dfrac{1}{C_{eq}}=\sum_{(i=1)}^n \dfrac{1}{C_i}$£.
