Formulario di fisica: le onde elettromagnetiche
Le onde elettromagnetiche sono una componente essenziale e onnipresente del nostro mondo: dalla luce visibile che illumina le nostre giornate alle onde radio che trasmettono musica e voce attraverso i nostri dispositivi elettronici. Il concetto di onda elettromagnetica si basa su un fenomeno fisico per cui l’energia si propaga attraverso lo spazio tramite campi elettrici e magnetici oscillanti. Queste oscillazioni seguono modelli precisi che possono essere descritti attraverso formule matematiche. Tali formule ci consentono di prevedere la frequenza, la lunghezza d’onda, l’energia e altre caratteristiche fondamentali delle onde elettromagnetiche.
Per esempio, la formula £$c = λν$£ (dove c è la velocità della luce, λ la lunghezza d’onda e ν la frequenza dell’onda) è un punto di partenza cruciale per analizzare le onde elettromagnetiche. Da qui, possiamo derivare altre equazioni che ci permettono di esplorare come le onde interagiscono con la materia, come sono generate e come possiamo sfruttarle per le nostre tecnologie.
Scopriamo insieme quali sono le formule principali che hanno a che fare con questo tema e, soprattutto, cos’è un’onda elettromagnetica e qual è la sua funzione!
- Definizione di onde elettromagnetiche
- Velocità di propagazione dell'onda elettromagnetica
- Vettore di Poynting
Definizione di onde elettromagnetiche
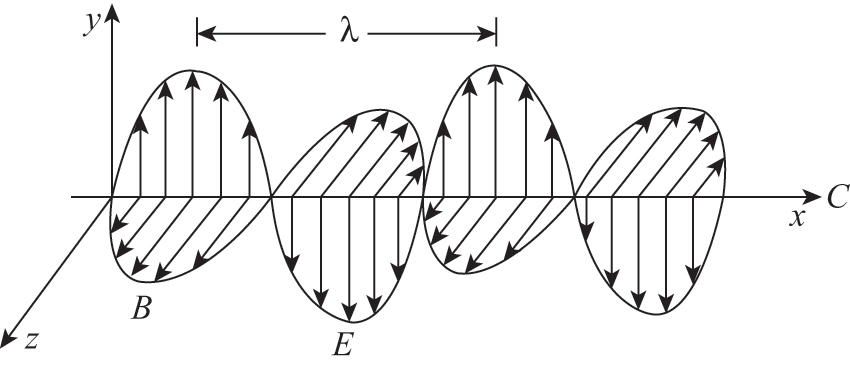
Le onde elettromagnetiche possono essere definite come delle oscillazioni del campo elettromagnetico, in cui direzione di propagazione dell’onda, direzione di oscillazione del campo magnetico e direzione di oscillazione del campo elettrico sono tutte perpendicolari tra loro. Un’onda di questo tipo si dice trasversale.
Ad esempio, se l’onda propaga lungo l’asse £$x$£, il campo elettrico oscilla parallelamente all’asse £$y$£ e il campo magnetico parallelamente all’asse £$z$£, le funzioni dei campi sono: $$E= E_0 \sin[k(x-vt)] \quad \text{e} \quad B= B_0 \sin[k(x-vt)] $$ dove £$E_0$£ e £$B_0$£ sono le ampiezze dei campi.
Inoltre: £${k=\dfrac{2\pi}{\lambda}}$£ è la costante di propagazione dell’onda, ovvero il numero di oscillazioni per unità di lunghezza moltiplicato per £$2\pi$£; £${v=\lambda f=\dfrac{\lambda}{T}}$£ è la velocità di propagazione dell’onda nel mezzo; £${\omega=2\pi f}$£ è la pulsazione dell’onda.
Velocità di propagazione dell’onda elettromagnetica
La velocità di propagazione dell’onda nel vuoto è £$c$£:
$$c=\frac{1}{\sqrt{\epsilon_0 \mu_0}}= \frac{E_0}{B_0} = \frac{E}{B}$$
La velocità di propagazione dell’onda in un mezzo è £$v$£:
$$ v=\frac{1}{\sqrt{\epsilon \mu}}= \frac{1}{\sqrt{\epsilon_0 \epsilon_r \mu_0 \mu_r}}= \frac{c}{\sqrt{\epsilon_r \mu_r}}$$
Vettore di Poynting
Il vettore di Poynting, così nominato in onore del fisico inglese John Henry Poynting che lo introdusse nel 1884, è un vettore utilizzato in elettromagnetismo che rappresenta la direzione e la grandezza del flusso di energia (potenza per unità di area) in un campo elettromagnetico. In altre parole, indica la direzione in cui l’energia si sta propagando e con quale intensità in un dato punto nello spazio.
Il vettore di Poynting indica la quantità di energia trasportata da un’onda elettromagnetica nell’unità di tempo e per unità di area ed è definito come:
$$\vec S= \frac{1}{\mu_0} \, \vec E \wedge \vec B$$
Il suo modulo è £$S={\frac{1}{\mu_0}} \, EB = {\frac{1}{c\mu_0}} E^2={\frac{c}{\mu_0}} B^2$£
Nel S.I. l’unità di misura è £${\dfrac{W}{m^2}}$£.
