Formulario di fisica: il moto rettilineo uniformemente accelerato
Il moto rettilineo uniformemente accelerato rappresenta uno dei concetti cardine nel mondo della fisica. Sin dagli albori dell’indagine scientifica, gli esseri umani hanno cercato di comprendere i movimenti degli oggetti che li circondano, e questo moto è stato uno dei primi a essere analizzato in dettaglio. Una pietra che cade, una macchina che accelera su una strada retta o un corpo che scivola su un piano inclinato senza attrito sono esempi tipici di questo tipo di movimento, e i principi che lo regolano si ritrovano in moltissime applicazioni pratiche e teoriche.
La caratteristica distintiva del moto rettilineo uniformemente accelerato è l’accelerazione costante: mentre in un moto rettilineo uniforme la velocità dell’oggetto rimane invariata nel tempo, nel moto uniformemente accelerato la velocità cambia in modo costante e prevedibile. Questa semplice ma potente idea ha portato alla derivazione di una serie di formule che permettono di calcolare distanze, velocità e accelerazioni in funzione del tempo.
Nel corso di questo articolo, scopriremo le formule fondamentali associate al moto rettilineo uniformemente accelerato, approfondendo come ogni variabile interagisca con le altre e come queste equazioni possano essere applicate in una varietà di scenari. Dalla teoria alla pratica, dal concetto alla formula, iniziamo!
- Definizione di moto rettilineo uniformemente accelerato
- Accelerazione media e accelerazione istantanea
- Le equazioni cinematiche del moto uniformemente accelerato
- Legge oraria del moto uniformemente accelerato
- Relazione tra £$s$£ e £$v$£
- Spazio come area
Definizione di moto rettilineo uniformemente accelerato
Un punto materiale si muove di moto rettilineo uniformemente accelerato se la traiettoria è una retta e se la sua velocità £$\vec v$£ varia in modo costante nel tempo, cioè l’accelerazione è costante.
Accelerazione media e accelerazione istantanea
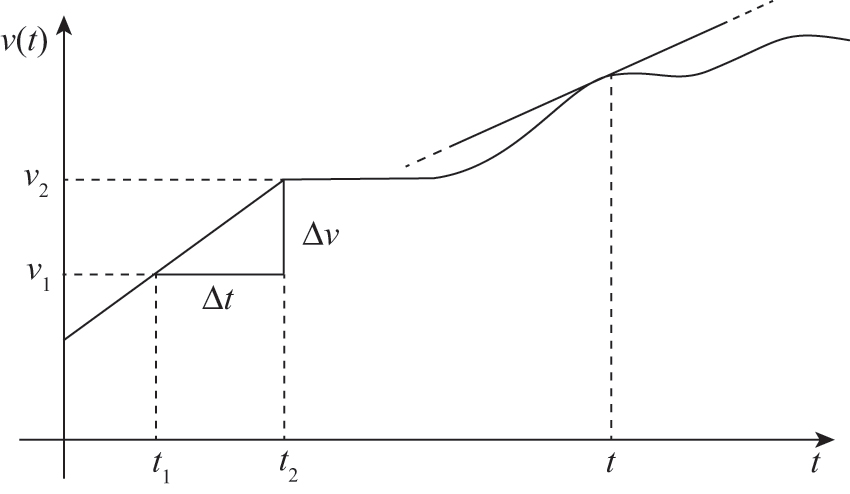
Si può ricavare graficamente il valore dell’accelerazione scalare media in un dato intervallo £$\Delta t$£, ricavando dal grafico velocità-tempo il valore della pendenza della retta passante per i due punti estremi dell’intervallo £$\Delta t$£.
L’accelerazione scalare istantanea corrisponde al valore della pendenza della retta tangente al grafico all’istante £$t$£.
Le equazioni cinematiche del moto uniformemente accelerato
[iol_placeholder type="formula" engine="katex" display="block-dollar"]\left\{ \begin{array}{ll}
a(t)=a \\
v(t)=at + v_{0}\\
s(t)=\frac{1}{2}at^2+v_{0}t+s_{0}
\end{array} \right.[/iol_placeholder]
dove £$v_{0}$£ e £$s_{0}$£ sono rispettivamente la velocità e la posizione del punto nell’istante iniziale £$t_{0}=0$£.
Legge oraria del moto uniformemente accelerato
£${a = \frac{dv}{dt} \qquad dv=adt \qquad v – v_{0} = \int_{t_0}^{t} adt = a(t-t_0)}$£ £${v = \frac{ds}{dt} \qquad ds=v(t)dt \quad s – s_{0} = \int_{t_0}^{t} [a(t-t_0)+v_0]dt = \frac{1}{2}a(t-t_0)^2 + v_0(t-t_0)}$£
Ponendo £$t_0=0$£ si ottengono le relazioni 1.2.
Relazione tra £$s$£ e £$v$£
Eliminando £$t$£ nelle equazioni di £$v(t)$£ e £$s(t)$£, si ottiene una relazione che lega £$s$£ e £$v$£:
$$s-s_0= \frac{v^2- v_0^2}{2a}$$
Spazio come area
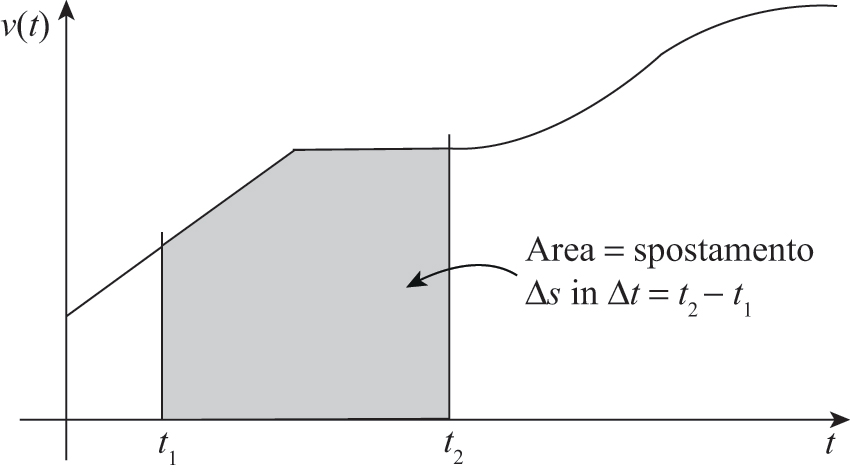
L’area sottesa al grafico velocità-tempo tra due istanti £$t_1$£ e £$t_2$£ corrisponde allo spostamento del punto materiale nell’intervallo £$\Delta t = t_2 – t_1$£.
