Definizione di trasformazioni di Lorentz
H.A. Lorentz scrisse le trasformazioni tra due sistemi di rifermento inerziali con effetti relativistici prima che Einstein sviluppasse la teoria della relatività; egli procedette per via teorica e formulò delle relazioni per le quali le equazioni di Maxwell risultassero invarianti.
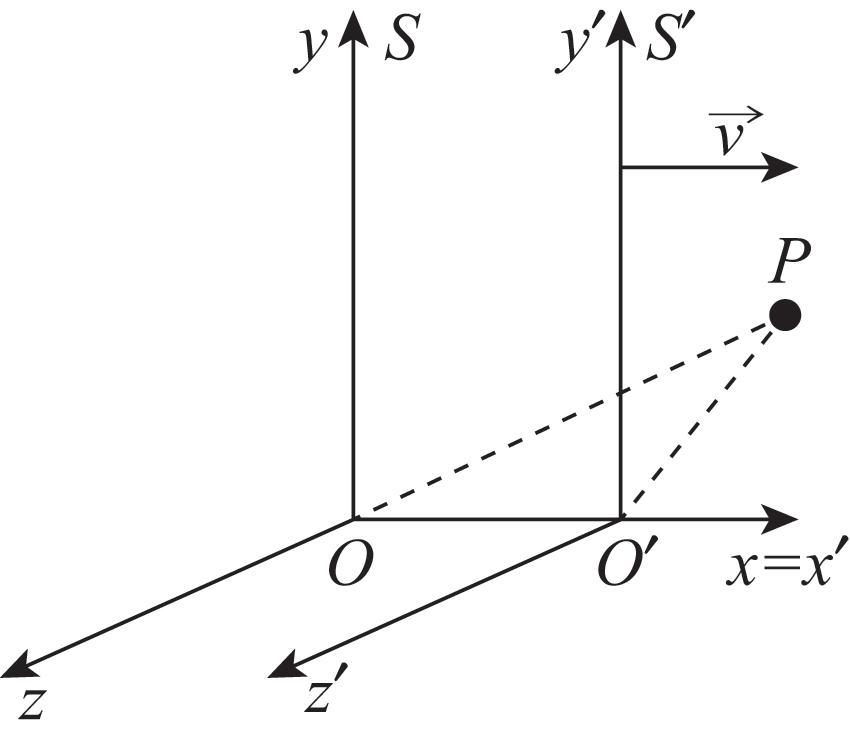
Dati due sistemi di riferimento inerziali £$S$£ e £$S’$£, con £$S’$£ in moto traslatorio uniforme con velocità £$\vec v$£ rispetto a £$S$£, le coordinate di un punto P sono uguali a £$(x,y,z,t)$£ in £$S$£ e £$(x’,y’,z’,t’)$£ in £$S’$£. Supponiamo per semplicità che gli assi £$y$£ e £$z$£ siano paralleli a £$y’$£ e £$z’$£ e che l’asse £$x$£ coincida con £$x’$£ che sia parallelo alla velocità £$\vec v$£, come illustrato in figura.
All’istante iniziale coincidono le origini dei due sistemi (£$O=O’$£) e il tempo (£$t=t’=0$£).
Le trasformazioni di Lorentz e le trasformazioni inverse tra le coordinate dei due sistemi sono le seguenti:
$$\left\{ \begin{array}{ll} x'=\frac{x-vt}{\sqrt{1-\frac{v^2}{c^2}}} = \gamma (x-vt) \\ y'=y\\ z'=z\\ t'=\frac{t-\frac{v}{c^2}x}{\sqrt{1-\frac{v^2}{c^2}}} = \gamma (t-\frac{\beta}{c}x) \end{array} \right. $$ $$ \left\{ \begin{array}{ll} x=\frac{x'+vt}{\sqrt{1-\frac{v^2}{c^2}}} = \gamma (x'+vt') \\ y=y'\\ z=z'\\ t=\frac{t'+\frac{v}{c^2}x'}{\sqrt{1-\frac{v^2}{c^2}}} = \gamma (t'+\frac{\beta}{c}x') \end{array} \right. $$
dove si è posto: $$\beta=\frac{v}{c} \quad \text{e} \quad \gamma=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}=\frac{1}{\sqrt{1-\beta^2}}$$
