Caricamento in corso...
Legge di Charles
In questa lezione potrai scoprire in cosa consiste la seconda delle tre leggi che derivano dalla formulazione più generale dell'equazione di stato dei gas perfetti: la legge di Charles.
Capirai sulla base di quali ipotesi risulta utilizzabile tale relazione e ne scoprirai la formulazione matematica. Così come per le altre leggi, capirai come, grazie al suo utilizzo, sia possibile rapportare tra loro la condizione iniziale e finale di una trasformazione.
Appunti
Molte delle trasformazioni subite dai gas perfetti posso essere definite isobare, ossia a pressione costante.
La legge di Charles è infatti una semplificazione dell'equazione di stato dei gas perfetti nella quale si considera che la pressione di un gas resti invariata. In tal caso saranno quindi solo temperatura e volume a variare nel tempo.
Contenuti di questa lezione su: Legge di Charles
Enunciato della legge di Charles
La legge di Charles descrive una trasformazione lungo cui, mantenendo la pressione costante, un gas può variare la sua temperatura ed il suo volume. Il grafico solitamente maggiormente utilizzato per rappresentare trasformazioni fisiche come questa riporta sui suoi assi pressione e volume: £$p-V$£. Rappresentandovi la legge di Charles otterremo una retta orizzontale che ci indicherà l'invariabilità della pressione, rappresentata sull'asse delle ordinate. Se il gas aumenta il suo volume, la sua temperatura tenderà a seguirlo, aumentando. Allo stesso modo, ad una diminuzione di volume corrisponderà una riduzione della temperatura del gas, il quale si starà muovendo da destra verso sinistra lungo la retta rappresentata.
In definitiva:
Se la pressione di un gas perfetto è costante, il suo volume e la sua temperatura risultano essere direttamente proporzionali.
Formulazione matematica della legge di Charles
La legge di Charles descrive una trasformazione a pressione costante. A partire dall'equazione di stato dei gas perfetti possiamo ricavarne la sua formulazione, svolgendo alcuni semplici passaggi:
£$pV = nRT$£
La costante dei gas £$R$£ è un valore numerico che non varia mai, indipendentemente dalle leggi studiate. In quanto tale, può quindi sempre essere considerato una costante:
£$pV = n \ cost \ T$£
Nelle trasformazioni di un gas che non comportano aggiunta o sottrazione di massa, anche il numero di moli non varierà mai, potrà quindi essere considerato costante e inglobato nel termine più generico £$cost$£:
£$pV = cost \ T$£
Da ultimo, è possibile inglobare anche la pressione nel termine generico £$cost$£. Data una trasformazione isobara come quella descritta dalla legge di Charles infatti, si può assumere che essa resti costante nel tempo. Per semplicità invertiamo prima la posizione dei termini di temperatura e di pressione nell'equazione:
£$pV = cost \ T$£
£$V = \dfrac{cost \ T}{p}$£
£$\dfrac{V}{T} = \dfrac{cost}{p}$£
Per poi inglobare, come già anticipato, la pressione nel termine costante £$cost$£:
£$\dfrac{V}{T} = cost$£
La precedente formulazione rappresenta la legge di Charles.
Trasformazione fisica e legge di Charles
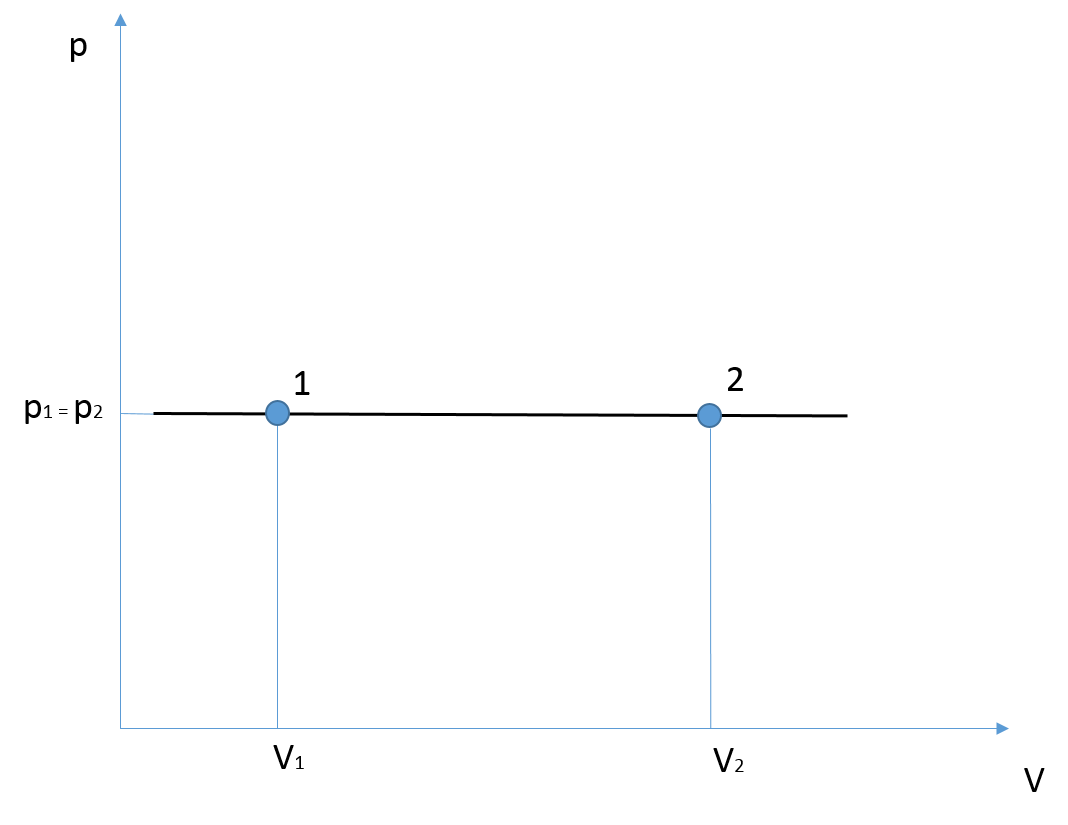
La legge di Charles descrive una trasformazione a pressione costante. Consideriamo un gas in una determinata condizione fisica £$1$£, esso subisce una trasformazione che lo porta allo stato £$2$£ muovendosi lungo un'isobara rappresentata da una retta orizzontale nel piano £$p-V$£, come già anticipato. La legge di Charles può essere riscritta specificando a quale stato ci si riferisce:
£$\dfrac{V_{1}}{T_{1}} = cost$£
£$\dfrac{V_{2}}{T_{2}} = cost$£
Il termine a destra delle uguaglianze esprime una costante, la stessa per entrambe le equazioni. In conclusione è possibile affermare che i due termini a sinistra siano uguali:
£$\dfrac{V_{1}}{T_{1}} = \dfrac{V_{2}}{T_{2}}$£
Come conseguenza, se si è in grado di caratterizzare completamente un gas nello stato iniziale o finale di una trasformazione isobara, conoscendo una sola quantità tra temperatura e volume relativa all'altro stato, sarà possibile calcolarsi la quantità mancante di quest'ultimo.
Legge di Charles: un esperimento
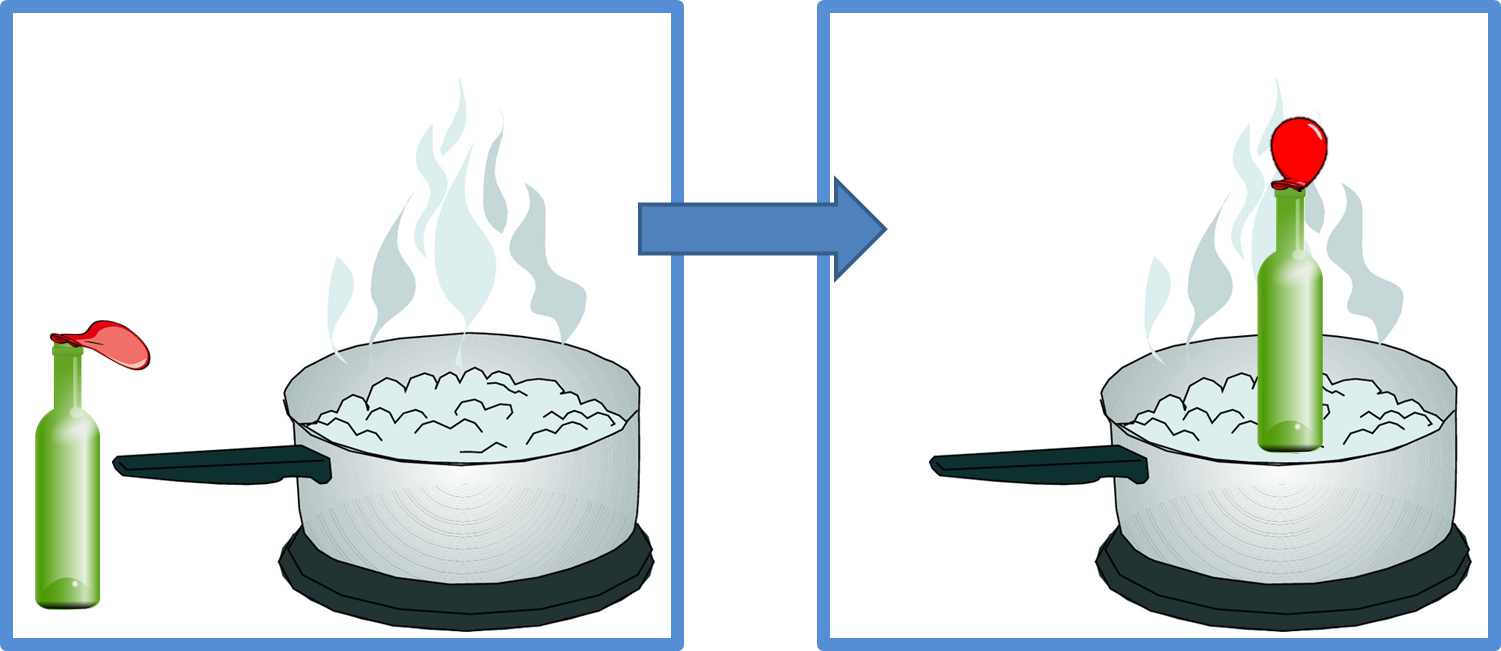
Proviamo ad immaginare di eseguire un esperimento che ci spieghi a fondo in cosa consiste la legge di Charles. Prendiamo un palloncino e avvolgiamolo intorno ad una bottiglia vuota in vetro. Posizioniamo la bottiglia in piedi all'interno di una pentola piena di acqua e poniamo quest'ultima sul fuoco. Il palloncino funzionerà da tappo e confinerà l'aria che sarà naturalmente presente all'interno della bottiglietta, impedendole di uscire. L'acqua presente nella pentola, che si scalderà per effetto del fornello acceso, andrà a scaldare anche l'aria presente all'interno della bottiglia. L'aria contenuta, comportandosi da gas perfetto, manterrà la sua pressione costante e pari a quella atmosferica che esiste all'esterno della bottiglia, per mantenere un equilibrio. Come conseguenza di ciò, a il gas ideale confinato all'interno della bottiglia cercherà di espandersi rispondendo all'aumento di temperatura. Il palloncino si gonfierà quindi, lasciando la possibilità all'aria contenuta di aumentare il suo volume.
Si tratta di un perfetto esempio di applicazione della legge di Charles, nella quale, a pressione costante, un aumento di temperatura comporta un aumento del volume di un gas ideale:
£$\dfrac{V}{T} = cost$£
