Le onde: le loro caratteristiche in fisica

Dal delicato fruscio del vento tra le foglie, prodotto dalle onde sonore, alle impercettibili onde elettromagnetiche che permettono la comunicazione dei nostri dispositivi, le onde sono una presenza costante nella nostra vita quotidiana. E poi ci sono le onde meno familiari ma altrettanto fondamentali, come le onde gravitazionali che, pur essendo state previste da Einstein un secolo fa, sono state rilevate solo di recente.

Ogni onda, indipendentemente dalla sua natura, possiede una serie di caratteristiche distintive: frequenza, lunghezza d’onda, ampiezza e velocità. Queste proprietà, pur sembrando termini tecnici, rivelano in realtà molto sull’essenza delle onde e sul loro comportamento. Ad esempio, la frequenza di un’onda ci dice quante volte essa vibra in un determinato lasso di tempo, mentre l’ampiezza ci fornisce informazioni sulla sua potenza o intensità.

Scopriamo insieme le loro caratteristiche generali!

• Definizione generale di onda in fisica
• Lunghezza d’onda, frequenza e velocità delle onde
• Onde in una corda
• Sovrapposizione e interferenza di onde

Definizione generale di onda in fisica

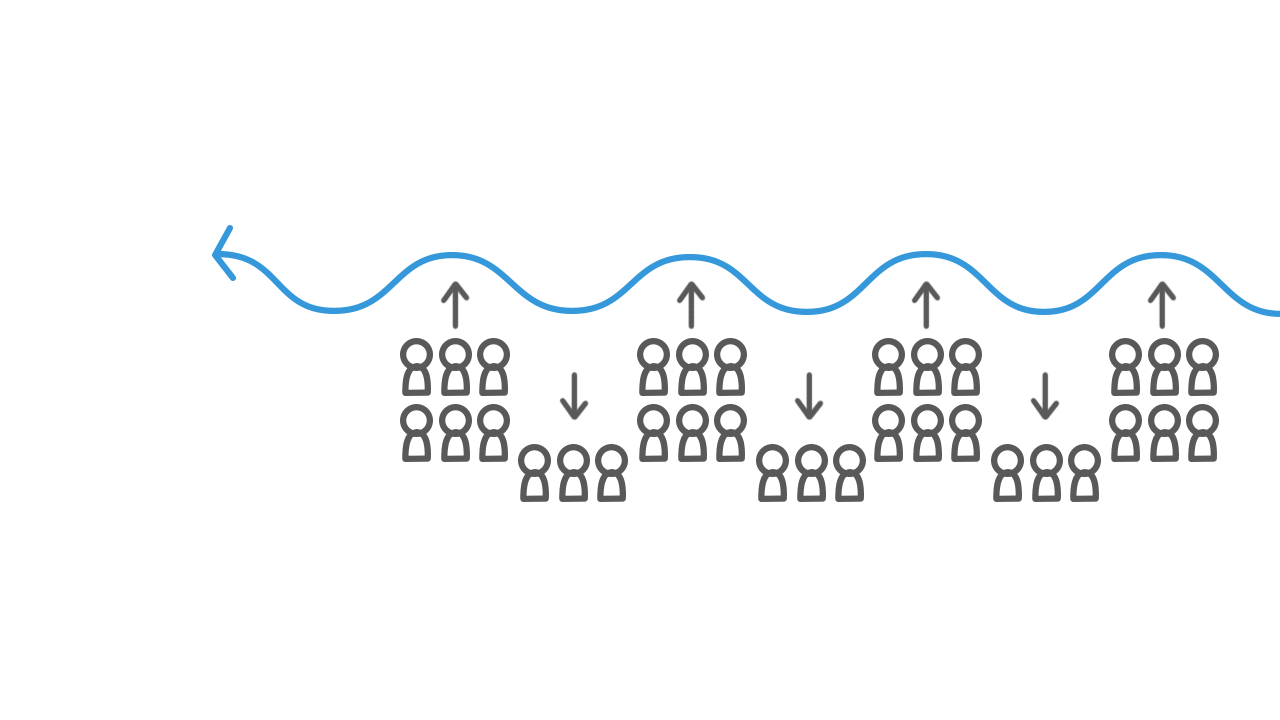
Delle spighe di grano che si muovono in un campo a causa dell’effetto del vento oppure dei tifosi allo stadio che incominciano a fare la “ola” sono tutte rappresentazioni di ONDE! Ma come può essere veramente definito questo fenomeno fisico?

Un’onda è una perturbazione che si propaga da un punto ad un altro dello spazio con una determinata velocità che dipende dalle caratteristiche del mezzo in cui avviene la propagazione (aria, acqua, il vuoto..) e trasportando una definita quantità di energia, ogni onda ne trasporta un tipo diverso.

Bisogna prestare attenzione quando si parla di onde, perché si può incappare in grosse incomprensioni! Ciò che è fondamentale, è saper distinguere il moto dell’onda nello spazio dal moto delle singole particelle che la compongono. Ad esempio, per citare le righe precedenti, i tifosi che iniziano a muoversi per creare la “ola”, si muovono ciascuno sul proprio posto, ma il moto dell’onda vero e proprio è il propagarsi della ola lungo l’intero stadio!

Per semplificare il tutto, le onde possono essere suddivise in due grandi categorie secondo il loro moto di propagazione:

• trasversali, quando lo spostamento delle particelle che compongono l’onda avviene nella direzione perpendicolare alla sua propagazione. Una corda che viene fatta oscillare muovendo una delle sue estremità è un’onda trasversale!
• longitudinali, quando lo spostamento delle particelle avviene nella stessa direzione della propagazione. Le onde sonore sono longitudinali!

Lunghezza d’onda, frequenza e velocità delle onde

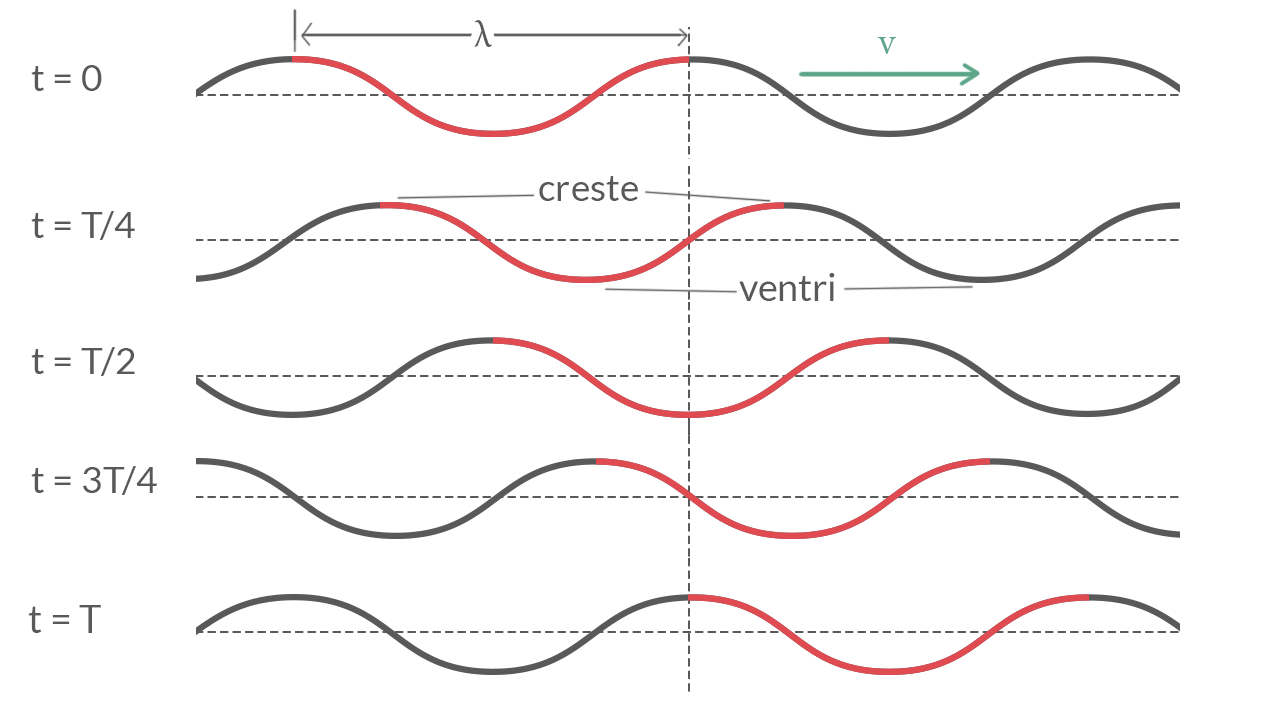
Le onde regolari e periodiche sono perturbazioni che si propagano da un punto ad un altro e che si ripetono uguali nel tempo e nello spazio.
Per queste onde è possibile definire ben determinate caratteristiche:

• l’ampiezza, il massimo spostamento dalla posizione di equilibrio (presa sulle ascisse di un piano cartesiano), sia verso l’alto che verso il basso
• le creste, i punti corrispondenti al massimo spostamento verso l’alto; i ventri quelli corrispondenti al massimo spostamento verso il basso
• la lunghezza d’onda £$\lambda$£ che nel Sistema Internazionale si misura in metri, è la distanza tra una cresta e quella successiva o tra un ventre e quello successivo
• il periodo £$T$£, l’intervallo di tempo dopo il quale l’onda si ripete uguale a se stessa. L’inverso del periodo, esattamente come accadeva nel moto armonico, è la frequenza £$f$£ (£$f = 1/T$£).

Utilizzando la definizione di velocità possiamo calcolare anche quella dell’onda:

£$v_{onda} = \frac{spazio \ percorso}{intervallo \ di \ tempo \ impiegato} = \frac {\lambda}{T} = \lambda \cdot f$£

La sua unità di misura è il metro al secondo(£$\frac{m}{s}$£).

Onde in una corda

La velocità di propagazione di un’onda in una corda dipende dalle caratteristiche del mezzo in cui si verifica l’onda.

In particolare, sono due le grandezze da tenere in considerazione quando l’onda si sposta lungo una corda o un qualsiasi altro mezzo lineare solido: la massa e la tensione.

Maggiore è la tensione in una corda e minore la sua massa, maggiore sarà la facilità con cui l’onda si propaga in essa e quindi maggiore sarà la sua velocità di propagazione.

ATTENZIONE! Quando parliamo di massa non intendiamo la massa totale della corda, ma la sua densità lineare £$\mu$£, cioè la massa per unità di lunghezza. In una corda leggera e lunga la velocità può essere la stessa di quella in una corda corta e pesante:

£$\mu = \frac{m}{L}$£

Dove: £$m$£= massa del mezzo £$L$£= lunghezza del mezzo

La sua unità di misura è il £$\frac{kg}{m}$£.

Grazie alla densità lineare possiamo calcolare la velocità dell’onda come:

£$v$£= £$\sqrt{\frac{F}{\mu}}$£

Dove: £$\mu$£= densità lineare della corda £$F$£= tensione del mezzo.

Sovrapposizione e interferenza di onde

Sovrapposizione

Fino ad ora abbiamo trattato unicamente situazioni in cui avevamo una sola onda, ma cosa succede quando due o più di loro si incontrano?

Si sovrappongono e interferiscono!

Durante la sovrapposizione, dovuta al passaggio di due o più onde in uno stesso mezzo di propagazione, le funzioni d’onda, che definiscono l’andamento di un’onda in un piano cartesiano, si combinano, dando come risultato una perturbazione totale della corda uguale alla somma delle funzioni d’onda coinvolte.

Immaginiamo di avere due onde in una corda, una avente funzione £$y_2$£ e l’altra £$y_1$£.

Nel momento in cui esse si trovano in una certa posizione £$x$£, la funzione d’onda risultante della perturbazione sulla corda è: £$y = y_1 + y_2$£ (guardare immagine 1).

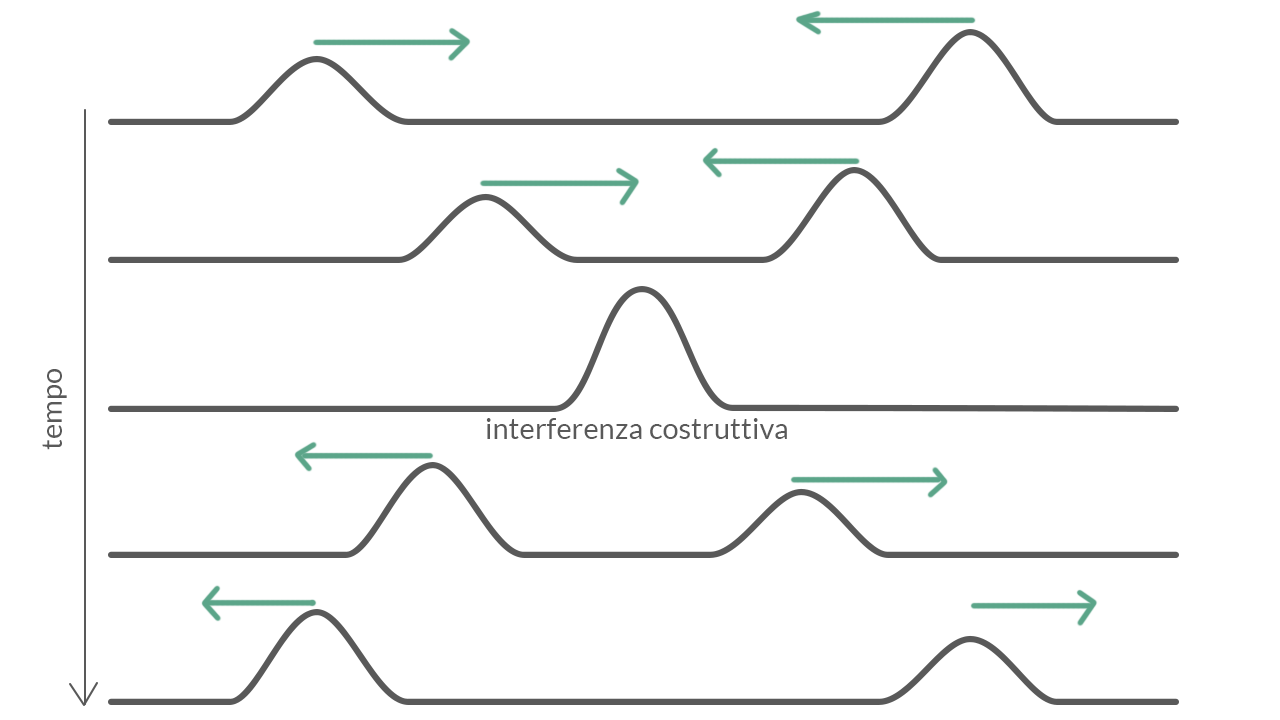
L’interferenza, invece, è quel fenomeno causato dal passaggio di due o più onde per uno stesso punto; si può definire anche come la conseguenza della sovrapposizione.

In questo caso si sommano le ampiezze!

Se gli impulsi sono in fase, cioè se le sorgenti emettono creste e ventri nello stesso istante, e le onde si muovono lungo la stessa direzione di uno stesso mezzo, si genera un’interferenza costruttiva per cui l’ampiezza dell’onda risultante è maggiore di quella delle singole onde.

Se gli impulsi sono in opposizione di fase, cioè quando una sorgente emette una cresta l’altra emette un ventre, si genera interferenza distruttiva per cui l’ampiezza dell’onda risultante è minore dell’ampiezza delle singole onde.

È importante sottolineare che esiste anche un altro metodo per determinare la tipologia di interferenza quando due o più onde non si muovono lungo la stessa direzione, come nel caso delle onde sonore. In particolare questo metodo è utilizzato per onde che si propagano in mezzi non solidi (aria, acqua).

Si ha interferenza costruttiva nei punti in cui la differenza di cammino, cioè la differenza tra le distanze di un punto dalle diverse sorgenti generatrici delle onde, è pari ad un multiplo intero della lunghezza d’onda (£$0\lambda$£, £$\lambda$£, £$2\lambda $£, £$3\lambda $£ …).

Si ha interferenza distruttiva nel punto in cui la differenza di cammino tra le sorgenti e il punto di sovrapposizione è un multiplo dispari di mezza lunghezza d’onda (£$\frac{\lambda}{2}$£, £$\frac{3}{2}\lambda$£, £$\frac{5}{2}\lambda$£ ecc.).