Caricamento in corso...
Le onde sonore
Perché ai concerti ci sentiamo tremare il petto e la pancia? La risposta è che anche la musica è un’onda! Scopri a cosa sono dovuti i suoni che percepiamo nella vita quotidiana e come possiamo studiarli!
Appunti
Il suono è un tipo di onda molto particolare che viaggia nell’aria facendone vibrare le molecole ad una velocità media di £$343 \frac{m}{s}$£. Nello spazio, dove non c’è il "vuoto", il suono non può propagarsi!
Scopri le caratteristiche delle onde sonore e tutti i fenomeni ad esse collegati: la frequenza, il livello di intensità e l’effetto Doppler!
Contenuti di questa lezione su: Le onde sonore
Caratteristiche del suono
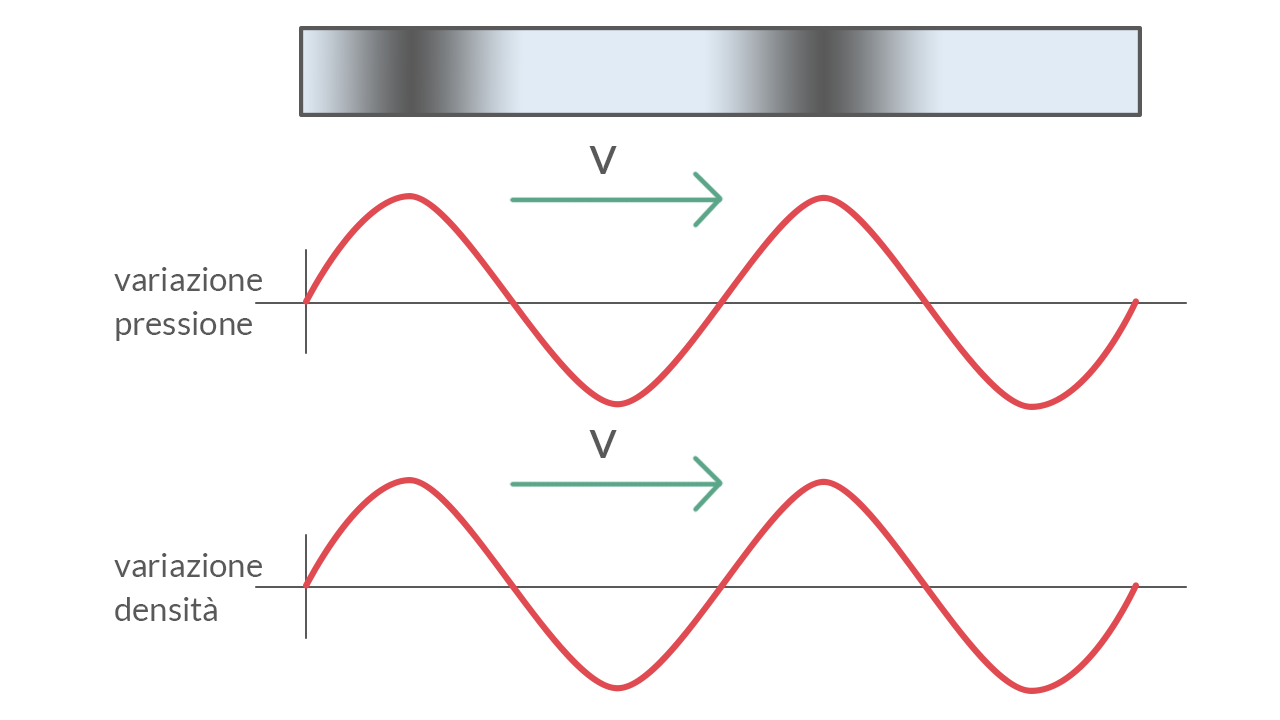
Il suono è un’onda longitudinale che si può propagare solo attraverso la materia.
Per muoversi, l’onda sonora sfrutta la compressione e l'espansione delle particelle presenti nell'aria provocando una variazione di pressione e quindi di densità del mezzo nei pressi della sorgente.
In condizioni atmosferiche standard, il suono si muove ad una velocità di £$343 \ \frac{m}{s}$£; la variazione di pressione e densità che provoca l’onda sonora può essere rappresentata su un piano cartesiano come una funzione sinusoidale.
La velocità di propagazione del suono dipende dalle caratteristiche del materiale in cui si muove l’onda. Hai mai provato a parlare sott’acqua? Chi prova ad ascoltare non sente niente! Questo accade perché l’acqua è 10 000 volte meno comprimibile dell’aria e quindi le onde sonore, dovute a variazioni di pressione e densità, si propagano molto più velocemente che nell’aria. Queste perturbazioni viaggiano a circa £$1484 \frac{m}{s}$£ in acqua e non riescono ad essere catturate dai nostri padiglioni auricolari.
Suoni con frequenza diversa vengono percepiti dal nostro orecchio in modo diverso, ciò significa che la frequenza determina il tono dell’onda. Per esempio, il primo tasto a sinistra del pianoforte ha una frequenza di £$55 \ Hz$£ mentre l’ultimo sulla destra ha una frequenza di £$4187 \ Hz$£.
L’orecchio umano è in grado di udire un intervallo di frequenze molto più ampio, da £$20 \ Hz$£ a £$20 \ 000 \ Hz$£. Onde sonore con frequenze maggiori sono definite ultrasuoni mentre quelle con frequenze inferiori sono dette infrasuoni.
Il suono è prima di tutto uno strumento della natura, infatti diverse specie animali sfruttano infrasuoni e ultrasuoni prodotti biologicamente. I pipistrelli utilizzano ultrasuoni per localizzare le prede al buio mentre le balenottere azzurre usano infrasuoni per comunicare a grandi distanze. Gli ultrasuoni sono utilizzati anche in medicina per terapie, producendo piccole onde d’urto, e per le ecografie, tramite macchine che emettono ultrasuoni e ne rilevano “l’eco” costruendo poi un’immagine del soggetto "colpito".
Un aspetto particolare delle onde sonore è che: la velocità in un certo mezzo è uguale per ogni frequenza.
Perciò, nella relazione £$v= \lambda f $£, se la frequenza dell'onda sonora aumenta, la sua lunghezza d’onda diminuisce perché la £$v$£ di propagazione resta costante.
L’intensità del suono
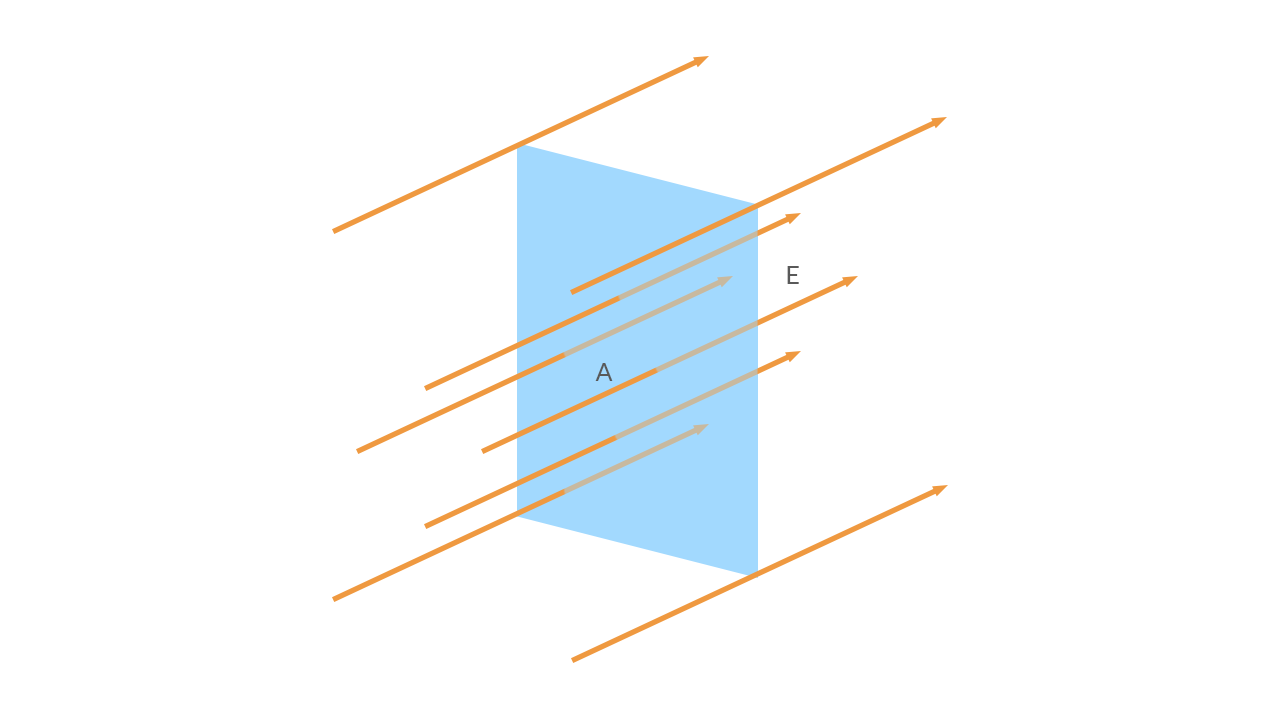
Cosa rende il rumore prodotto da un martello pneumatico e il cinguettio di un uccellino così diversi?
La risposta è: l'intensità del suono, cioè la quantità di energia trasportata dall’onda sonora che insiste su un'unità di superficie in un tempo £$t$£!
£$I = \frac{E}{A \cdot t}$£
Ricordando che la potenza è data dal rapporto tra l’energia e l’intervallo di tempo in cui essa viene sviluppata, possiamo scrivere:
£$I = \frac{P}{A}$£
Infatti, nel Sistema Internazionale, l’intensità si misura in £$\frac{Watt}{m^2}$£.
Per semplificare il discorso, possiamo prendere in considerazione una sorgente puntiforme di superficie £$4\pi r^2$£ e scrivere l’intensità con la seguente formula:
£$I = \frac{P}{4\pi r^2}$£
Il concetto di intensità può essere esteso a tutti i tipi di onda!
La percezione umana del suono e il livello di intensità
L’orecchio umano è molto più sensibile di quanto si pensi.
Siamo in grado di udire suoni estremamente deboli, come un respiro, dell’ordine di £$10^{-11} \frac {W}{m^2}$£, e di sopportare rumori molto elevati, come la musica di un concerto di intensità £$ 1 \ \frac{W}{m^2}$£
Un altro aspetto molto interessante è il modo con il quale percepiamo il volume di un suono. Supponiamo, ad esempio, di sentire prima un suono di intensità £$I_1$£ e successivamente di sentirne un altro di intensità £$I_2$£ che sembra avere un'intensità doppia della prima. Misurando i valori di £$I$£, otterremo che £$I_2$£, in realtà, è approssimativamente 10 volte £$I_1$£. Ciò significa che la nostra percezione del suono è tale che, un aumento uniforme del volume, corrisponde a intensità che crescono in base ad un fattore moltiplicativo.
Per tale ragione è stata istituita una scala, chiamata livello di intensità, che misura il volume di un suono secondo il logaritmo in base 10 di £$I$£ percepita sulla minima intensità percepibile dall’orecchio umano.
$$\beta = (10 \ dB) \ \log\left(\frac{I}{I_0}\right)$$
Dove £$I_0$£ è la più debole intensità che l’orecchio umano possa udire, vale a dire £$10^{-12} \frac{W}{m^2}$£.
Nel Sistema Internazionale il livello di intensità si misura in decibel (dB), che risulta essere una grandezza adimensionale, dato che le uniche dimensioni presenti nella sua definizione sono le intensità che, infine, si semplificano.
Vuoi ripassare i logaritmi? Vai alla lezione da qui!
L’effetto Doppler
Osservatore in movimento e sorgente ferma
Sorgente in movimento e osservatore fermo
Sorgente e osservatore in movimento relativo
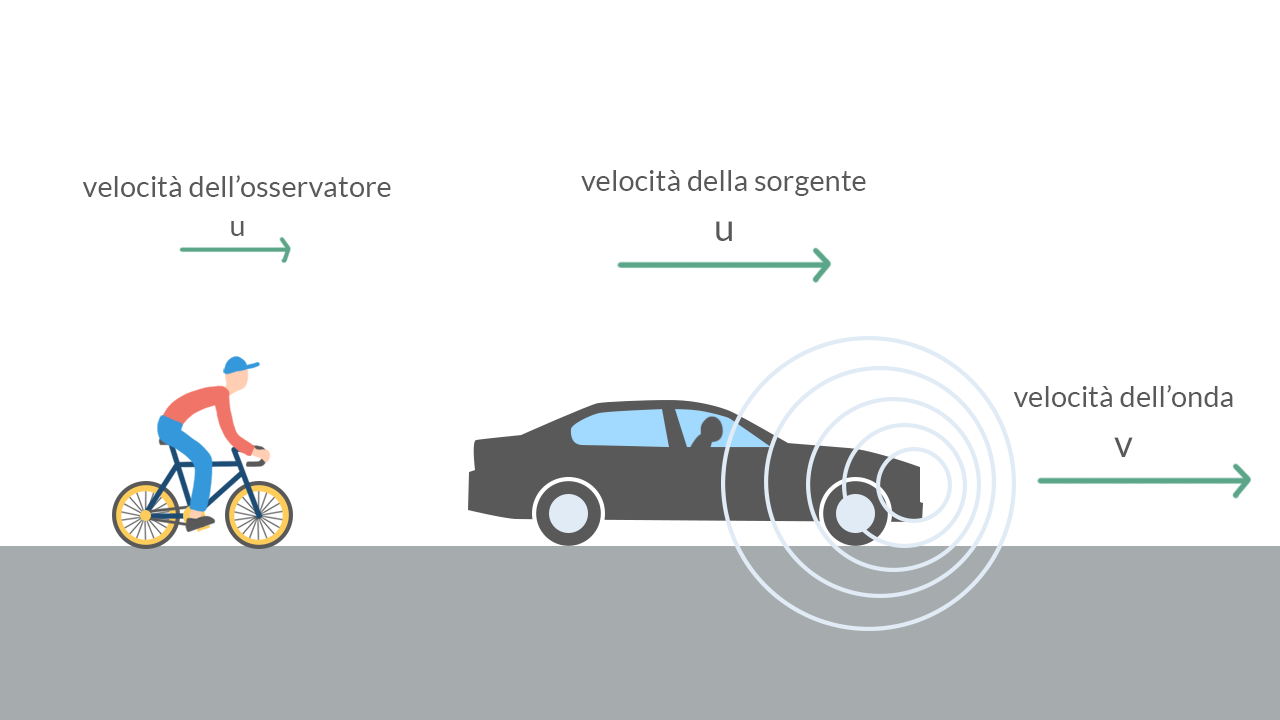
L’effetto Doppler consiste nella variazione di percezione di tono, ovvero di frequenza, di un’onda sonora dovuta al moto relativo della sorgente e dell’osservatore. Tale fenomeno è proprio di tutte le onde; anche la luce presenta un suo effetto Doppler particolare, chiamato “redshift”, usato in particolare in astrofisica per calcolare la velocità dei corpi luminosi. Questo fenomeno consiste nello spostamento del colore della luce verso il rosso o verso il blu in relazione al movimento della sorgente luminosa.
Per quanto riguarda il suono invece, le situazioni possono essere distinte in 3 diversi fenomeni.
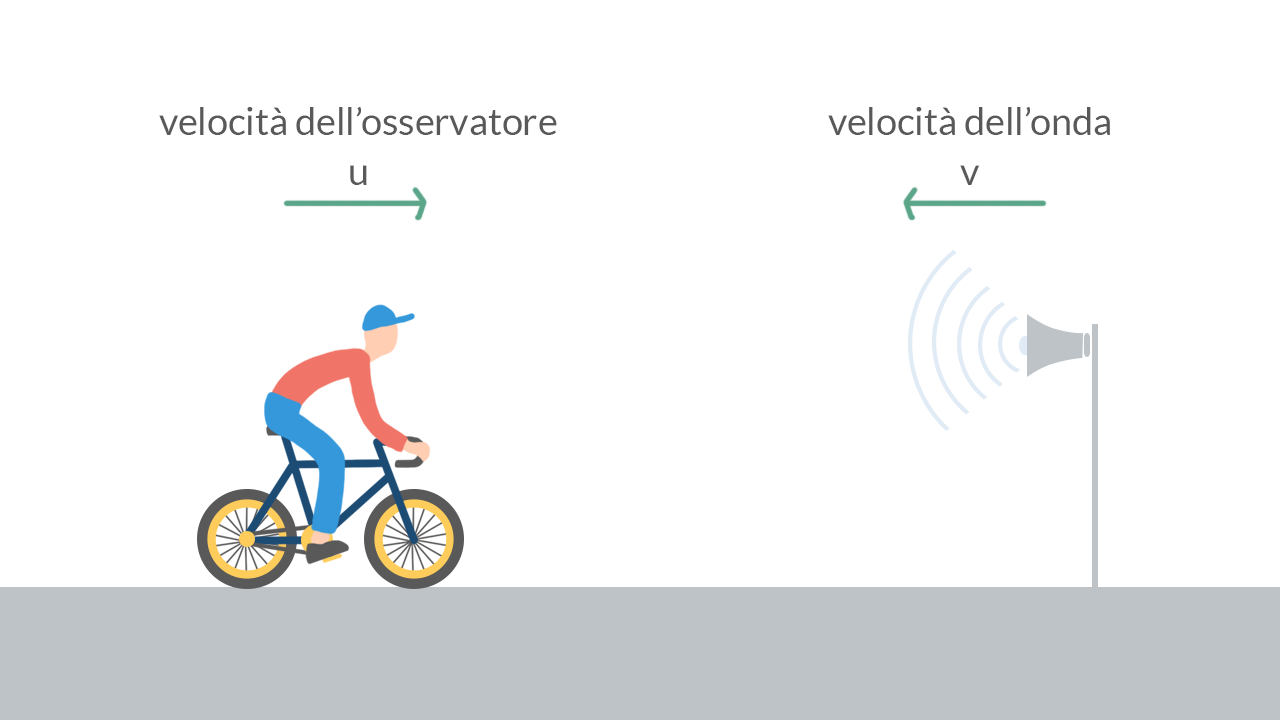
1) Osservatore in movimento e sorgente ferma:
Prendiamo un uomo che si muove alla velocità £$v$£ verso una sorgente sonora stazionaria, la quale emette onde che viaggiano alla velocità £$u$£. Secondo l’osservatore, la velocità del suono risulta £$v \ ’ = v + u$£ (composizione galileiana delle velocità); ciò significa che l’ascoltatore, in un definito intervallo di tempo, viene investito da più compressioni, cioè da una minore lunghezza d’onda, di quante non ne incontrerebbe se fosse fermo. Una lunghezza d’onda minore significa percepire una frequenza £$f’$£ maggiore della £$f$£ reale della sorgente.
Per l’osservatore in moto, la frequenza percepita varia per effetto Doppler secondo: £$f’ = (1 \pm \frac{u}{v}) \ f$£.
Il segno “+” viene utilizzato quando l’osservatore si avvicina alla sorgente; il segno “-” si usa quando l’osservatore si allontana dalla sorgente.
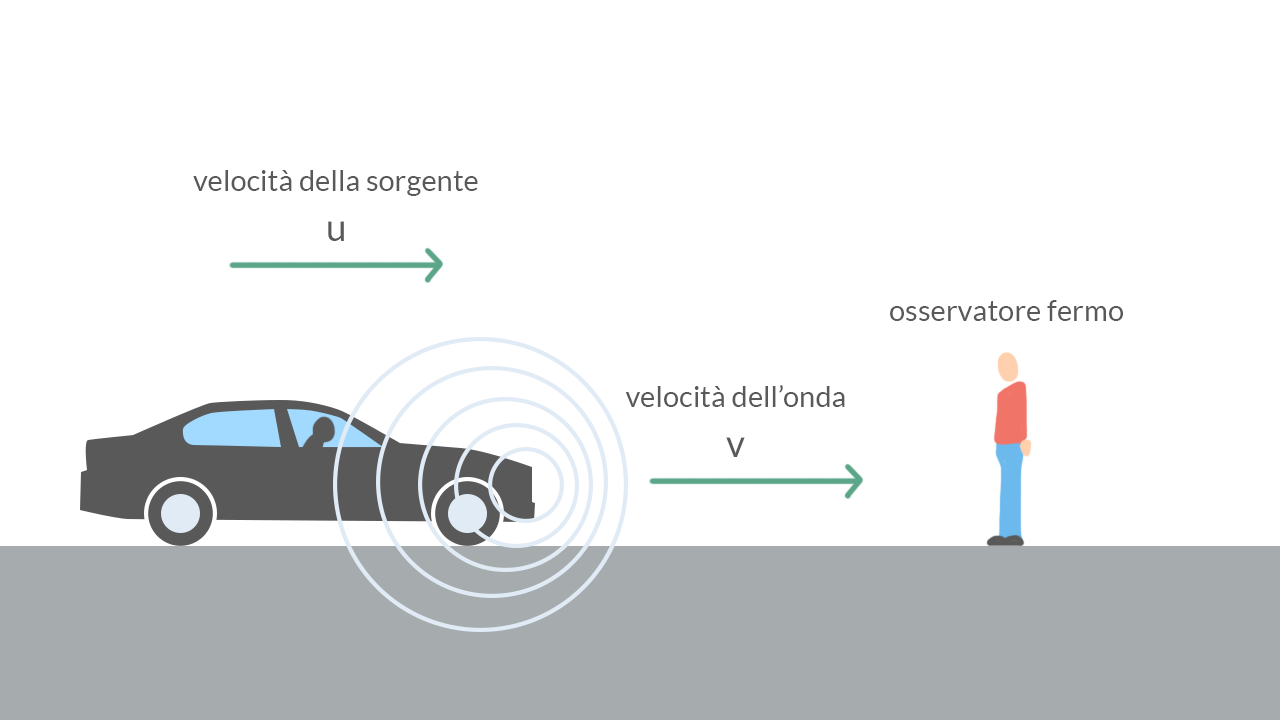
2) Sorgente in movimento:
Consideriamo ora un’ambulanza che si muove verso di noi con una velocità £$u$£. Per via del suo moto, la lunghezza d’onda e quindi la frequenza delle onde sonore percepite da noi, come si vede nell’immagine 2, risultano minori rispetto a quelle che avrebbero se la sorgente fosse ferma.
Questo ci permette di affermare che l’osservatore, in un definito intervallo di tempo, incontra un numero maggiore di compressioni in uno stesso intervallo di tempo, dunque percepisce una frequenza £$f’$£ più elevata di quella reale £$f$£.
A causa del moto della sorgente, l’osservatore percepisce una frequenza che, per effetto Doppler, risulta: £$f’ = \left(\frac {1}{1 \pm \frac{u}{v}}\right) \ f$£
In questo caso, al contrario del precedente, il segno “+” si usa quando la sorgentesi allontana dall’osservatore e il segno “-” quando si avvicina.
Caso generale:
I risultati ottenuti fino ad ora possono essere combinati al fine di ottenere una formula che descriva il caso in cui siano sia la sorgente che l’osservatore a muoversi.
Se indichiamo con £$u_s$£ la velocità della sorgente e con £$u_o$£ quella dell’osservatore, possiamo scrivere:
$$f’ = \left(\frac {1 \pm \frac {u_o}{v}}{1 \mp \frac{u_s}{v}}\right) \ f$$
Al numeratore possiamo trovare il caso in cui l’osservatore si muove verso la sorgente(+) e quando si allontana(-) e al denominatore quello in cui la sorgente si muove verso l’osservatore(-) e quando si allontana(+).
