La cinematica di base: elementi e nozioni
La cinematica di base è il primo ramo della fisica ad essere studiato, perché consente di studiare il moto e il movimento dei corpi, perciò ci consente di determinare tutta una serie di formule e di leggi che descrivono il movimento anche senza prendere in considerazione l’elemento che l’ha causato.
Si contrappone per questo alla dinamica: perché quest’ultima studia proprio le cause del movimento, cioè le forze che l’hanno reso possibile; la cinematica, invece, si occupa di descrivere il moto dei corpi.
In questo articolo scopriremo proprio quali sono gli elementi principali della cinematica e cos’è più nel dettaglio!
- Cos'è la cinematica
- Il movimento di un punto materiale
- Il vettore posizione, il vettore spostamento e la traiettoria
- La velocità
- Diversi modi per esprimere la velocità
Cos’è la cinematica
La cinematica è la branca della fisica che si occupa di studiare il movimento dei corpi, cioè il loro moto. Un corpo, infatti, può essere definito in movimento quando nel tempo la sua posizione e le sue coordinate subiscono una variazione. Se, invece, queste restano invariate, allora il corpo sarà in una condizione di quiete e non di movimento.
Il moto è relativo: dipende dal sistema di riferimento e dall’osservatore. Ad esempio, quando siamo su un veicolo in movimento, guardando dal finestrino ci sembrerà di starci muovendo, ma se provassimo guardare il sedile su cui siamo seduti, invece, ci sembrerebbe di essere fermi.
Il movimento di un punto materiale
La cinematica studia come cambia nel tempo la posizione di un oggetto.
Ogni corpo occupa un volume, perciò ogni corpo di forma irregolare dovrebbe essere molto difficile da studiare. Ma quando la distanza che questo corpo percorre è molto maggiore rispetto al suo volume, quest’ultimo diventa trascurabile.
Quindi il movimento di un corpo si può rappresentare come il movimento di un punto materiale.
Il sistema di riferimento cartesiano è il metodo migliore per studiare il moto di un punto. Il sistema di riferimento è costituito da:
- 3 assi cartesiani, perpendicolari tra loro
- metro, per misurare le distanze
- cronometro, per misurare il tempo.
Il vettore posizione, il vettore spostamento e la traiettoria
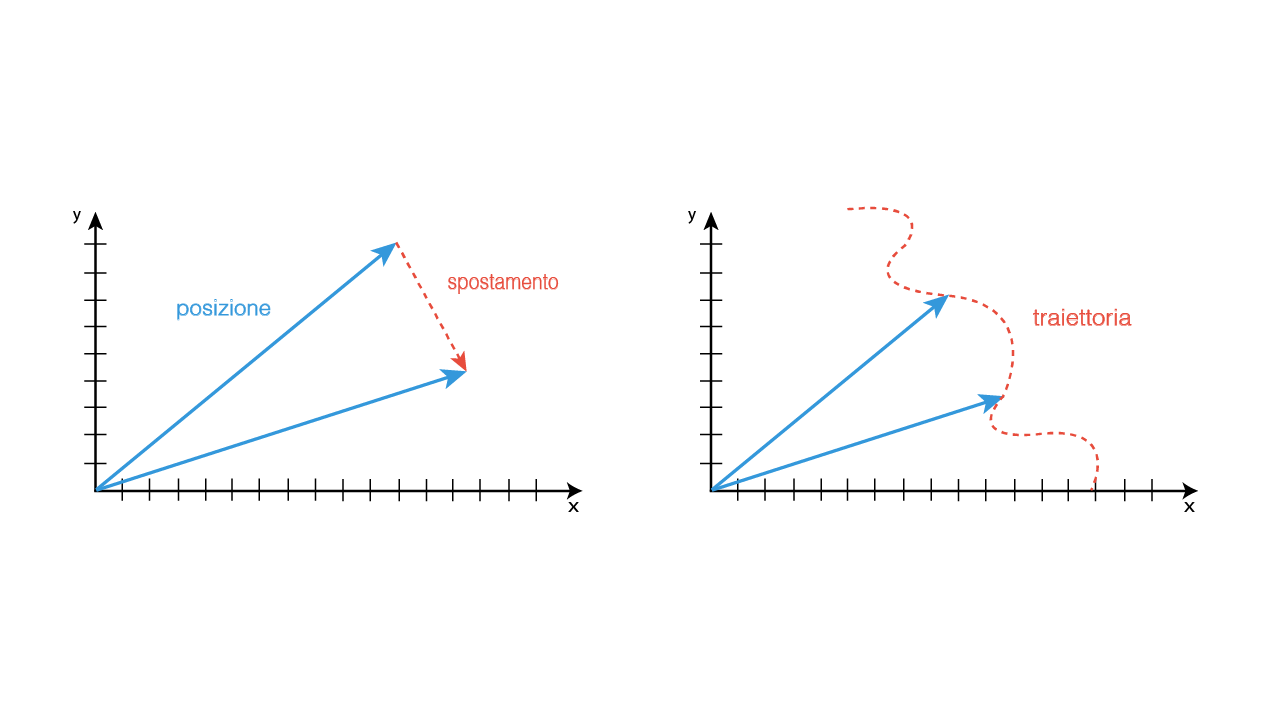
Quando parliamo di spazio dobbiamo tenere in considerazione alcune grandezze vettoriali.
Il vettore posizione è quel vettore che ha come:
- direzione la retta che congiunge l’origine (O) del sistema di riferimento e il punto (P) dove si trova il corpo,
- verso da O a P
- modulo la distanza tra i due punti in £$\text{m}$£.
Il vettore spostamento (£$\Delta{s}$£), invece, è la differenza di due vettori posizione. Quindi ha come:
- direzione la retta che congiunge i due punti £$P_1$£ (posizione iniziale) e £$P_2$£ (posizione finale);
- verso da £$P_1$£ a £$P_2$£
- modulo la distanza tra £$P_1$£ e £$P_2$£.
La traiettoria è, invece, quella linea (non per forza retta) che congiunge tutti i punti in cui si trova il corpo nei vari momenti.
È molto importante, quando si ha a che fare con lo spazio, specificare direzione e verso.
Esempio.
Se cerco il mio amico Andrea, con cui ero fino a cinque minuti fa, e lui mi dice che si trova a £$200 \ \text{m}$£ dal punto in cui era prima, mi deve specificare anche la direzione e il verso, solo così posso trovarlo!
La velocità
Una delle grandezze principali che vengono ricavate dal tempo e dallo spazio è la velocità, definita come il tasso di cambiamento della posizione di un corpo in funzione del tempo.
La velocità è un vettore che ha la stessa direzione e lo stesso verso del vettore spostamento, e il suo modulo varia a seconda del tipo di velocità considerata e anche dal tipo di moto.
La velocità media (£$v_m$£) di un punto materiale si definisce come il rapporto tra la distanza percorsa e l’intervallo di tempo impiegato; praticamente rappresenta in quanto tempo un corpo percorre una distanza £$ \Delta s$£. La velocità media è valida per qualsiasi tipo di moto.
Esempio: £$\Delta{s}$£ = £$34,5 \ \text{m}$£ £$\Delta{t}$£ = £$12\ \text{s}$£ £$V_m$£ =£$ \frac{34,5 \ m}{12 \ s}$£= £$2,875 \ \frac{\text{m}}{\text{s}}$£
La velocità istantanea ( £$\vec{v_i}$£ ), invece, si calcola diversamente a seconda del tipo di moto e definisce la velocità di un corpo in un preciso istante di tempo, prima o dopo il quale il corpo può aver avuto un’altra velocità qualsiasi.
Diversi modi per esprimere la velocità
L’unità di misura della velocità secondo il Sistema Internazionale è £$\frac{\text{m}}{\text{s}}$£.
L’unità di misura più usata quotidianamente è £$\frac{\text{km}}{\text{h}}$£.
Come trasformare l’unità di misura usata quotidianamente in quella usata dal SI? Come trasformare £$\frac{\text{km}}{\text{h}}$£ in £$\frac{\text{m}}{\text{s}}$£ ?
Un chilometro (£$\text{km}$£) equivale a £$10^{3} \ \text{m}$£ mentre un’ora a £$3{,}6 \cdot 10^{3} \ \text{s}$£ (60 minuti da 60 secondi).
Per trasformare i £$\frac{\text{km}}{\text{h}}$£ in £$\frac{\text{m}}{\text{s}}$£ basta moltiplicare tutto per £$\frac{10^{3} \ \text{m}}{3{,}6 \ \cdot \ 10^{3} \ \text{s}}$£, il che equivale a dividere il valore della velocità per £$3{,}6$£ trasformando tutto in £$\frac{\text{m}}{\text{s}}$£.
Esempio.
Un Frecciarossa in media viaggia a £$300 \ \frac{\text{km}}{\text{h}}$£, a quanti £$\frac{\text{m}}{\text{s}}$£ sta viaggiando?
£$300 \ \text{km}$£ = £$300 \ \cdot \ 10^{3} \ \text{m}$£
£$1 \ \text{h}$£ = £$3{,}6 \ \cdot 10^{3 } \ \text{s}$£
Quindi £$300 \ \frac{km}{h}$£ = £$\frac{300 \ \cdot \ 10^{3} \ \text{m}}{3{,}6 \ \cdot \ 10^{3} \ \text{s}}$£ = £$\frac{300 \ \text{m}}{3{,}6 \ \text{s}}$£ = £$83{,}333333333 \ \frac{\text{m}}{\text{s}}$£
