Il moto armonico: definizione e legge oraria
Il moto armonico è una particolare tipologia di moto rettilineo e può essere definito come la proiezione del moto di un corpo che segue un moto circolare uniforme. Si tratta di un moto oscillatorio, periodico come il moto circolare uniforme.
In questo articolo potrai imparare tutto quello che c’è da sapere: cos’è il moto armonico, come si definisce, quali sono le formule e qual è la sua legge oraria!
- Cos'è il moto armonico
- Come ottenere il moto armonico
- Il valore della velocità massima del moto armonico
- Il valore dell'accelerazione massima del moto armonico
- Come si rappresenta il moto armonico sul piano cartesiano
- Dimostrazione delle leggi del moto armonico
Cos’è il moto armonico
Il moto armonico, appunto, è un moto di tipo oscillatorio, periodico proprio come il moto circolare uniforme. Possiamo definirlo come il moto della proiezione di un punto P, che si muove in moto circolare uniforme attorno ad una circonferenza.
In particolare, mentre il punto P ruota seguendo una traiettoria curvilinea, la sua proiezione che potremmo chiamare Q e che di fatto segue invece il moto armonico, continua ad oscillare tra i due estremi del diametro della stessa circonferenza.
Si tratta proprio di una oscillazione, infatti la velocità della proiezione raggiunge il massimo al centro ed è nulla agli estremi del diametro, dove il punto Q inverte il suo moto e cambia direzione. Invece, l’accelerazione è nulla al centro e massima agli estremi.
Come ottenere il moto armonico
Il moto oscillatorio regolare si chiama moto armonico.
Esempio.
Appendiamo ad una molla attaccata al soffitto un pesetto: se spingiamo il pesetto verso il basso osserviamo che la molla oscilla. Prima si muove verso il basso, poi, dopo aver raggiunto una lunghezza massima, torna verso l’alto. Il moto della molla compie oscillazioni regolari in tempi regolari, fino a fermarsi per attrito.
Il moto armonico è la proiezione di un punto che si muove di moto circolare uniforme su un diametro della circonferenza stessa.
La proiezione è il segmento perpendicolare a un diametro £$PQ$£ che unisce un punto £$A$£, appartenente alla circonferenza, ad un punto £$B$£ sul diametro.
Riprendendo l’esempio iniziale, gli estremi del diametro sono corrispondenti al punto più alto e più basso raggiunti dal pesetto mentre il centro della circonferenza corrisponde al centro del moto.
Il valore della velocità massima del moto armonico
Nel centro della circonferenza la velocità del moto assume il massimo valore possibile ed è equivalente alla velocità tangenziale del punto sulla circonferenza corrispondente perché in questo punto la direzione del vettore velocità è una retta parallela al diametro considerato, perciò la proiezione di un vettore parallelo al diametro su quest’ultimo sarà uguale al vettore stesso.
La velocità massima è pari al rapporto tra la circonferenza e il periodo.
£$v_{max}$£ = £$\frac{2\pi r}{T}$£
Nella rappresentazione precedente la velocità massima è raggiunta nel punto £$O$£.
La velocità massima si mantiene costante ad ogni oscillazione se si suppone che l’attrito dell’aria sia nullo (caso ideale).
Negli estremi del diametro considerato la velocità è nulla, ovvero di 0 £$\frac{\text{m}}{\text{s}}$£, perchè in quei punti la direzione del vettore velocità è perpendicolare al diametro.
Il valore dell’accelerazione massima del moto armonico

Se la proiezione di un vettore tangente alla circonferenza è massima al centro e nulla agli estremi, quella di un vettore diretto verso il centro è nulla al centro e massima agli estremi. Questo perché il vettore accelerazione ( £$\vec{a}$£ ) e il vettore velocità ( £$\vec{v}$£ ) nel moto circolare uniforme sono perpendicolari!
Nel moto armonico l’accelerazione agli estremi misura £$\frac{v^2}{r}$£ oppure £$\omega^{2}\cdot r$£, infatti agli estremi l’accelerazione del punto £$B$£ sul diametro è equivalente all’accelerazione centripeta del punto £$A$£ corrispondente sulla circonferenza.
Come si rappresenta il moto armonico sul piano cartesiano
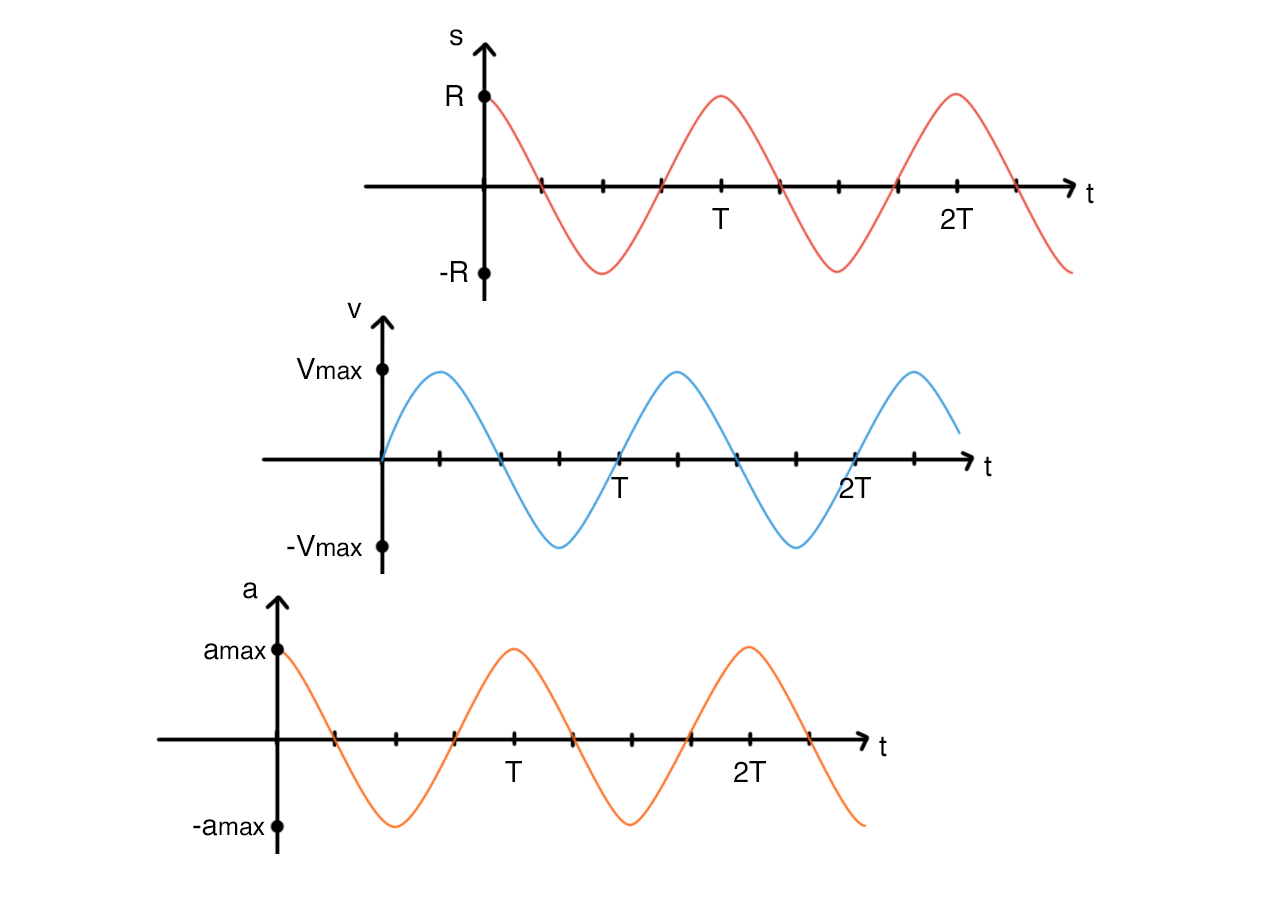
Anche il moto armonico di un punto può essere rappresntato su un piano cartesiano.
In un ipotetico grafico spazio-tempo, dove in £$t = 0$£ il punto si trova sull’estremo £$P$£, il moto da origine ad una cosinusoide, con periodo uguale al periodo del moto (£$T$£), e ampiezza (£$R$£) equivalente al raggio £$r$£ della circonferenza considerata.
La legge oraria è £$S$£ = £$R \cos(\theta)$£ dove £$S$£ è la distanza di B dal centro e £$\theta$£ è l’angolo compreso tra uno dei due raggi del diametro £$PQ$£ e il raggio a cui appartiene il punto £$A$£ sulla circonferenza. Dato che £$\theta$£ è uguale al prodotto £$\omega \cdot t$£ la legge oraria si può scrivere anche: £$S = R\cos(\omega t)$£.
Si considera positivo il valore di £$S$£ quando B è compreso tra £$P$£ e £$O$£, negativo quando è compreso tra £$O$£ e £$Q$£.
Per trovare il valore della velocità in un qualsiasi punto del moto si utilizza la legge: £$v = R\omega \sin(\omega t)$£ che rappresenta una sinusoide, nel grafico velocità-tempo, dove la velocità massima è £$\omega r$£, cioè la velocità tangenziale del punto £$A$£.
Si considera positivo il valore della velocità quando il punto B si muove da £$P$£ a £$Q$£, negativo se si muove nel senso opposto. La sinusoide passa per l’origine e infatti quando £$t = 0$£ e £$S = 0$£.
L’accelerazione agli estremi, invece, è massima, quindi nel grafico accelerazione-tempo il moto rappresenta una cosinusoide, e la legge è:
£$a = \omega^{2}R\cos{(\omega t)}$£ dove il valore massimo dell’accelerazione è £$\omega^{2} r$£ cioè l’accelerazione centripeta del punto £$A$£.
Si considera positivo il valore dell’accelerazione quando il punto £$B$£ è compreso tra £$P$£ e £$O$£, negativo se si trova dall’altra parte del diametro rispetto al centro.
Dimostrazione delle leggi del moto armonico
Le leggi enunciate precedentemente possono essere dimostrate con la trigonometria:
la legge oraria, la distanza £$BO$£ di £$B$£ dal centro £$O$£, è un cateto del triangolo rettangolo £$A \stackrel\triangle{O} B$£, quindi il rapporto tra la distanza £$BO$£ e il raggio £$AO$£ è equivalente al coseno dell’angolo £$\theta$£:
£$\frac{OB}{AO} = \cos{(\theta)}$£
Il vettore velocità (£$\vec{v_B}$£) del punto B, se traslato, forma con il vettore £$\vec{v_A}$£ un triangolo rettangolo simile ad £$A \stackrel\triangle{O} B$£ per il primo criterio dei triangoli, poiché £$\vec{v_A}$£ è perpendicolare a £$\vec{r}$£ ed il lato £$CD$£ è parallelo a £$AB$£. Quindi i triangoli hanno tutti gli angoli congruenti, e £$\theta$£ corrisponde all’angolo £$A\hat{C}D$£. Il rapporto tra la velocità del moto armonico e la velocità tangenziale di A è uguale al seno dell’angolo £$\theta$£:
£$\frac{v_B}{v_A} = \text{sen}{(\theta)}$£.
Il vettore accelerazione del punto £$A$£ (£$\vec{a_A}$£) è parallelo al raggio £$OA$£, mentre l’accelerazione di £$B$£ (£$\vec{a_B}$£) è parallela al segmento £$OB$£. Quindi anche quest’ultimo triangolo formato dai vettori accelerazione è simile ad £$A \stackrel\triangle{O} B$£ e £$\theta$£ è compreso tra il vettore £$\vec{a_A}$£ ed il vettore £$\vec{a_B}$£. Quindi:
£$\frac{a_B}{a_A} = \text{cos}{(\theta)}$£.
L’accelerazione di £$B$£ si trova con: £$\vec{a_B}$£ = £$\omega^2R\text{cos}{(\omega t)}$£, ma £$R\text{cos}{(\omega t)}$£ è uguale alla distanza (£$s$£) dal centro £$O$£, quindi l’accelerazione si può trovare anche con: £$a_B$£ = £$\omega^{2} s$£
