Moto rettilineo uniformemente accelerato: definizione e formule
Il moto rettilineo uniformemente accelerato è un moto nel quale un corpo si muove lungo una retta, mantenendo sempre una accelerazione costante.
Possiamo definire il moto come uniformemente accelerato se il corpo mantiene l’accelerazione costante, mentre se avviene lungo una linea retta possiamo definirlo non soltanto uniformemente accelerato, ma anche rettilineo.
Utilizziamo la parola uniformemente proprio per intendere che l’accelerazione non cambia, né aumenta, né diminuisce e resta sempre costante. Cerchiamo di capire meglio insieme quali sono le definizioni e come riconoscere il moto rettilineo uniformemente accelerato.
- Cos'è l'accelerazione
- Caratteristiche del vettore accelerazione
- La legge oraria nel moto uniformemente accelerato
- Il grafico spazio-tempo del moto rettilineo uniformemente accelerato
- Il grafico velocità-tempo del moto rettilineo uniformemente accelerato
- Dimostrazione della legge oraria
- Formulario per il moto rettilineo uniformemente accelerato
- Legge oraria della caduta di un capodoglio
Cos’è l’accelerazione
La velocità di un oggetto non è sempre costante, ma può diminuire o aumentare.
Esempio.
- Una bicicletta che corre su una strada a velocità costante ha un moto uniforme (grafico spazio-tempo: retta)
- Un pallone che rimbalza ha un moto vario (grafico spazio-tempo: non è una retta).
Per studiare i moti dove la velocità varia (moto vario) è necessario introdurre una nuova grandezza: l’accelerazione (£$\vec{a}$£).
L’accelerazione è una grandezza che ha come unità di misura £$\frac{\text{m}}{\text{s}^2}$£.
L’accelerazione è una grandezza vettoriale che misura la variazione della velocità nell’unità di tempo.
Prima di proseguire, vai a ripassare i concetti di base sui vettori.
Caratteristiche del vettore accelerazione

Il vettore accelerazione ha:
- direzione del vettore velocità (quindi uguale allo spostamento)
- verso uguale a quello della velocità se l’accelerazione è positiva
- oppure verso opposto a quello della velocità se l’accelerazione è negativa.
Quando un corpo diminuisce la sua velocità:
- il vettore spostamento e il vettore velocità sono concordi,
- il vettore accelerazione, invece, è discorde agli altri due, dato che la differenza di velocità £$V_f-V_i$£ è negativa.
Esempio.
Se l’accelerazione di una macchina è + £$3,5 \ \frac{\text{m}}{\text{s}^2}$£ vuol dire che la sua velocità sta aumentando; se, invece essa misura £$– 3,5 \ \frac{\text{m}}{\text{s}^2}$£ allora la velocità della macchina sta diminuendo.
Il modulo del vettore accelerazione varia a seconda del tipo di moto. Nel moto rettilineo uniformemente accelerato l’accelerazione è costante in ogni punto e il suo modulo equivale al rapporto tra la variazione della velocità e la variazione del tempo:
£$a$£ = £$\frac{\Delta{v}}{\Delta{t}}$£.
In qualsiasi moto l’accelerazione media (£$a_m$£) è uguale a £$\frac{\Delta{v}}{\Delta{t}}$£.
La legge oraria nel moto uniformemente accelerato
Il moto rettilineo uniformemente accelerato è un moto dove la traiettoria è una linea retta e l’accelerazione è costante in ogni punto.
La legge oraria in un moto rettilineo uniformemente accelerato con partenza da fermo è: £$S$£ = £$\frac{at^2}{2}$£
Esempio.
Se £$t$£ = £$2 \ \text{s}$£, £$a$£ = £$2 \ \frac{\text{m}}{\text{s}^2}$£ e il corpo ha velocità iniziale uguale a 0 perché parte da fermo, allora $$S=\frac{2 \ \frac{\text{m}}{\text{s}^2} \ \cdot \ 2^{2} \ \text{s}^2}{2}=4 m$$
Se, invece, il corpo sta viaggiando con una velocità costante diversa da £$ prima di intraprendere un moto uniformemente accelerato è necessario tenere in considerazione il fatto che è partito con una velocità iniziale diversa da [iol_placeholder type="formula" engine="katex" display="inline"/].
In un moto rettilineo uniformemente accelerato con partenza con velocità iniziale diversa da 0 la legge oraria è [iol_placeholder type="formula" engine="katex" display="inline"]S$£ = £$\frac{at^2}{2}$£ + £$v_0 \ \cdot \ t$£ con £$v_0$£ = velocità iniziale.
Esempio.
Se £$t$£ = £$2 \ \text{s}$£, £$a$£ = £$2 \ \frac{\text{m}}{\text{s}^2}$£ e £$v_0$£ = £$7 \ \frac{\text{m}}{\text{s}}$£
allora £$S$£ = £$\frac{2 \ \frac{\text{m}}{\text{s}^2} \ \cdot \ 2^2 \ \text{s}^2}{2}$£ + £$7 \ \frac{\text{m}}{\text{s}} \ \cdot \ 2 \ \text{s}$£ = £$4 \ \text{m}$£ + £$14 \ \text{m}$£ = £$18 \ \text{m}$£
La legge oraria vale anche in caso di accelerazione negativa.
In un moto curvilineo l’accelerazione istantanea non è uguale a quella del moto rettilineo uniformemente accelerato dato che quando sono presenti delle curve entra in gioco un altro tipo di accelerazione: l’accelerazione centripeta.
Il grafico spazio-tempo del moto rettilineo uniformemente accelerato
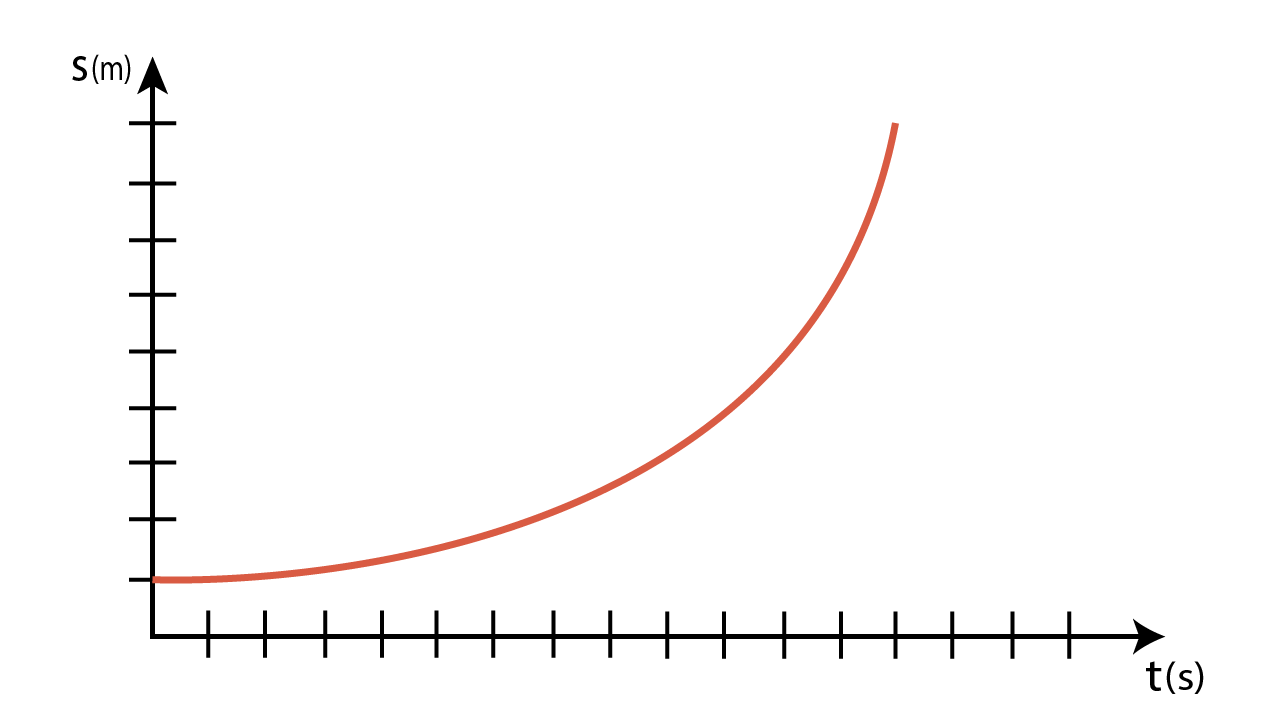
Anche il moto rettilineo uniformemente accelerato si può rappresentare su un piano cartesiano spazio-tempo. Non è identificato da una retta, ma da un ramo di parabola.
Infatti, mettendo lo spazio in funzione del tempo, si trova un’equazione di secondo grado:
£$S$£ = £$\frac{at^2}{2}$£ se £$v_0 = 0$£
£$S$£ = £$\frac{at^2}{2}$£ + £$v_0 \ \cdot \ t$£ se £$v_0 \ne 0$£
Il grafico velocità-tempo del moto rettilineo uniformemente accelerato

Se, invece, mettiamo la velocità sulle ordinate troveremo una retta. Infatti l’accelerazione si trova facendo il rapporto £$\frac{\Delta{v}}{\Delta{t}}$£, quindi l’equazione di questa retta è
£$v_f$£ = £$a \ \cdot \ t$£ + £$v_0$£
L’accelerazione è il coefficiente angolare della retta. Maggiore è l’accelerazione, maggiore è la inclinazione verso l’asse y della retta (sempre che si usino le stesse unità per le ascisse e per le ordinate).
Variazione di velocità e variazione di tempo sono direttamente proporzionali e la loro costante è l’accelerazione.
Se £$v_0=0$£, la retta passa per l’origine,
Se £$v_0 \neq 0$£, la retta interseca l’asse y nel punto £$(0; v_o)$£.
Dimostrazione della legge oraria
Velocità iniziale uguale a 0
Velocità iniziale diversa da 0
Proviamo a capire perché la legge oraria del moto rettilineo uniformemente accelerato è £$S$£ = £$\dfrac{at^2}{2}$£ + £$v_0 \ \cdot \ t$£
Abbiamo detto che nel grafico velocità-tempo lo spazio è uguale all’area sottostante la funzione, quindi se la funzione è una retta che passa per l’origine (£$v_0 = 0$£) l’area sotto la funzione sarà uguale all’area del triangolo rettangolo che ha per cateti £$\Delta{v}$£ e £$\Delta{t}$£.
Per calcolare la sua area si userà l’equazione £$S$£ = £$\dfrac{\Delta{v} \ \cdot \ \Delta{t}}{2}$£,
ma siccome £$\Delta{v}$£ = £$a \ \cdot \ t$£ allora possiamo scrivere:
£$S$£ = £$\dfrac{at^{2}}{2}$£
Se £$v_0$£ £$\ne$£ 0 allora la retta intersecherà l’asse delle y nel punto £$(0;v_o)$£ e quindi l’area sottostante la funzione sarà un trapezio con basi £$v_0$£ e £$v_f$£ e altezza £$\Delta{t}$£ . Quindi l’area si calolerà:
£$A$£ = £$\dfrac{(v_f + v_0) \ \cdot \ t}{2}$£
Ma £$v_f$£ = £$v_0$£ + £$\Delta{v}$£, quindi l’equazione si può scrivere: £$S$£ = £$\dfrac{(2v_0 + \Delta{v}) \ \cdot \ \Delta{t}}{2}$£ e quindi
£$S$£ = £$\dfrac{at^2}{2}$£ + £$v_0 \ \cdot \ t$£
Nel caso in cui il resto del problema ci fornisca £$v_0$£, £$v$£ e £$t$£, possiamo trovare lo spazio percorso usando l’area del trapezio: £$s= \dfrac{v_0 + v_f}{2} t$£
Formulario per il moto rettilineo uniformemente accelerato
Proviamo a fare un elenco di tutte le formule del moto rettilineo uniformemente accelerato viste fino ad ora:
Legge oraria della velocità: £$v=v_o+at$£
Non è altro che un modo alternativo di scrivere la definizione di accelerazione: £$a=\dfrac{v-v_o}{t}$£
La legge oraria della velocità è rappresentata da una retta nel grafico velocità-tempo, dove l’accelerazione è il coefficiente angolare e lo spazio percorso può essere ricavato come area sottesa dal grafico ovvero, nel caso generale, come area del trapezio rettangolo:
£$s=\dfrac{v+v_o}{2} t$£
Legge oraria: £$\Delta{s}=v_ot+\frac{1}{2}at^2$£
Dalla definizione di accelerazione: £$a=v-v_ot$£, possiamo ricavare il tempo £$t=v-v_oa$£ e sostituirlo nella formula dello spazio percorso come area sottesa dal grafico:
£$s=\dfrac{v+v_o}{2} \cdot \dfrac{v-v_o}{a} \Rightarrow s=\dfrac{v^2-v_o^2}{2a}$£
Legge oraria della caduta di un capodoglio
Uno degli effetti collaterali dell’utilizzo del motore a improbabilità infinita, la forma di propulsione utilizzata dai protagonisti della “Guida Galattica per Autostoppisti”, è il manifestarsi di fenomeni, nello spazio, caratterizzati da altissima improbabilità, come la materializzazione di un capodoglio a molte miglia (nel Sistema Internazionale diremmo “a molti chilometri”) dalla superficie di un pianeta. Lo sventurato animale, appena venuto al mondo, ha a malapena il tempo di diventare consapevole di sé prima di schiantarsi rovinosamente al suolo dopo una vertiginosa caduta, governata dall’attrazione gravitazionale del pianeta in questione. Ma andiamo con ordine, e permettiamo ancora una volta a un cetaceo di spiegarci un argomento di fisica.
Ammettiamo di materializzarci a nostra volta accanto al capodoglio, al sicuro nella nostra astronave dotata di motore a improbabilità infinita, e dotati di un cronometro per misurare il tempo, di un tachimetro per misurare la velocità e di un sonar per misurare la posizione.
Indichiamo con £$t_0$£ e £$x_0$£ il tempo e la posizione iniziale del moto del capodoglio, ossia l’istante e il luogo in cui il malcapitato cetaceo si materializza, nell’atmosfera del pianeta.
Poiché su questo pianeta si può fare un dispetto alla fisica e materializzarsi, ma l’attrazione gravitazionale funziona esattamente come sulla Terra, l’animale comincerà a precipitare verso il suolo: possiamo segnare, misurando £$i$£ volte, coppie di dati posizione/tempo (£$x_i, t_i$£) e/o coppie di dati velocità/tempo (£$v_i, t_i$£), allo scopo di individuare la legge oraria del capodoglio in caduta libera.
Legge oraria di un capodoglio in caduta: moto uniformemente accelerato
Le coppie di dati (£$x_i, t_i$£) ci mostrano come posizioni più lontane dal punto di partenza (e più vicine al suolo) vengono raggiunte sempre più velocemente dal capodoglio in caduta; le coppie di punti (£$v_i, t_i$£), confermano questa misurazione, dicendoci che la velocità aumenta, uniformemente, quanto più ci avviciniamo al suolo.
Esiste quindi un’accelerazione costante, che è proprio l’accelerazione gravitazionale caratteristica del pianeta sul quale ci troviamo.
Descriviamo la velocità del capodoglio in caduta: ad ogni istante £$t$£, £$v(t) = v_0+a\cdot t$£, dove £$v_0$£ è la velocità iniziale (che può essere posta uguale a zero, nel momento della materializzazione del capodoglio) e £$a$£ è l’accelerazione gravitazionale presente sul pianeta.
Qual è la legge oraria che descrive la caduta del capodoglio, ossia la legge che mette in relazione la sua posizione £$x$£ al tempo trascorso £$t$£ per tutto il tempo trascorso da £$t_0$£ a £$t$£, partendo dalla posizione £$x_0$£?
Integrando sull’intervallo di tempo da £$t_0$£ a £$t$£, e utilizzando la relazione £$v = \frac xt$£, otteniamo che
£$x(t) = x_0 + v_0\cdot t +\frac 12 \cdot a\cdot t^2$£
Il secondo membro a destra dell’equazione, £$v_0\cdot t$£, è naturalmente £$=0$£ se poniamo la velocità iniziale del capodoglio uguale a £$0 \frac ms$£. Analogamente, se decidiamo di far coincidere con la posizione £$=0$£ il dato £$x_0$£, anche £$x_0 = 0 m$£.
Prova a disegnare i grafici anche tu:
Il grafico (£$x_i, t_i$£) mostra che posizioni più avanzate, ossia più vicine alla rovinosa fine della vita del capodoglio, vengono raggiunte più velocemente: la curva si piega verso l’alto.
Il grafico (£$v_i, t_i$£) mostra invece una linea retta. Così come avveniva per il moto rettilineo uniforme, ove ottenevamo una retta il cui coefficiente angolare era la velocità costante del moto, nel caso della caduta libera del capodoglio otteniamo una retta, il cui coefficiente angolare è l’accelerazione costante del moto: nel caso specifico, la costante gravitazionale del pianeta sul quale ci troviamo.
