L'equilibrio dei solidi: quali sono le condizioni
L’equilibrio dei corpi è un concetto chiave in fisica che descrive lo stato di un corpo quando le forze agiscono su di esso in modo tale che la sua velocità rimanga costante. Quando parliamo di equilibrio, ci riferiamo spesso a due tipi: equilibrio statico e equilibrio dinamico.
L’equilibrio statico si verifica quando un corpo è a riposo e le forze esterne bilanciano esattamente l’effetto delle forze interne, senza alcuna accelerazione. L’equilibrio dinamico, invece, si verifica quando un corpo si muove con una velocità costante, e le forze che agiscono su di esso si bilanciano in modo che non ci sia accelerazione.
Un caso interessante di equilibrio è quando un corpo è posto su un piano inclinato. Mettere in equilibrio un corpo su un piano inclinato richiede una comprensione di come le forze agiscono su un oggetto su una superficie inclinata. Le forze principali coinvolte in questa situazione sono la forza gravitazionale, la forza normale (perpendicolare alla superficie del piano) e, se c’è attrito, la forza di attrito.
Per mantenere il corpo in equilibrio su un piano inclinato, le componenti delle forze devono essere bilanciate in modo che non ci sia alcuna accelerazione netta. Ciò può richiedere una configurazione particolare o l’uso di supporti o contropesi per bilanciare le forze.
Il concetto di equilibrio dei corpi e il problema specifico del corpo su un piano inclinato sono temi affascinanti che toccano molte aree della fisica, dall’ingegneria alla meccanica. In questo articolo, esploreremo in dettaglio come si analizzano e si bilanciano queste forze, con particolare attenzione alla realizzazione pratica dell’equilibrio in varie situazioni, come l’equilibrio di un corpo su un piano inclinato. Pronti? Cominciamo!
- Condizioni di equilibrio di un punto materiale e di un corpo rigido
- Baricentro o centro di massa nell'equilibrio dei solidi
- Il momento di una forza
- Momento di una coppia di forze nell'equilibrio dei solidi
- Equilibrio di un solido su un piano inclinato
- Modulo delle componenti della forza peso per l'equilibrio dei solidi
- Come mettere in equilibrio un solido su un piano inclinato
Condizioni di equilibrio di un punto materiale e di un corpo rigido
Un corpo si dice in equilibrio statico quando è fermo e continua a stare fermo.
Nel caso di un punto materiale, ovvero di un oggetto piccolo rispetto all’ambiente in cui si trova, esso è fermo se la somma di tutte le forze è uguale a 0.
Un punto materiale si trova in equilibrio quando la risultante £$F_{tot}$£ di tutte le forze è nulla, quindi uguale a £$0 \ \text{N}$£.
Ma le cose cambiano quando consideriamo un corpo rigido, ovvero un oggetto esteso che non subisce deformazioni quando gli vengono applicate delle forze.
Un corpo rigido, invece, è in equilibrio quando la somma vettoriale delle forze applicate è uguale a £$0 \ \text{N}$£ e quando la somma vettoriale di tutti i momenti delle forze ad esso applicate è uguale a £$0 \ \text{N} \cdot m$£.
Quindi un corpo rigido è in equilibrio quando: £$\begin{cases} \vec{F_{tot}} = 0 \\ \vec{M_{tot}} = 0 \end{cases}$£
Baricentro o centro di massa nell’equilibrio dei solidi
Il baricentro, chiamato anche centro di massa, è il punto geometrico corrispondente al valor medio della distribuzione della massa del corpo, o del sistema, nello spazio. Per questo motivo risulta essere il punto di applicazione della forza-peso di un corpo rigido. Nel caso particolare di un corpo rigido, infatti, il centro di massa ha una posizione fissa rispetto al sistema.
In particolare, se un corpo ha una forma regolare (es. sfera, cubo…) il suo centro di massa corrisponde al centro geometrico del corpo. Se un corpo è simmetrico ed omogeneo (stessa densità in ogni punto), il baricentro corrisponde con il suo centro di simmetria.
Una forza che agisce su un corpo rigido con…
- la sua direzione che passa per il baricentro, provoca un movimento traslatorio (sempre se non ci sono vincoli, cioè ostacoli)
- la sua direzione che non passa per il baricentro, provoca un movimento rotazionale.
Il momento di una forza
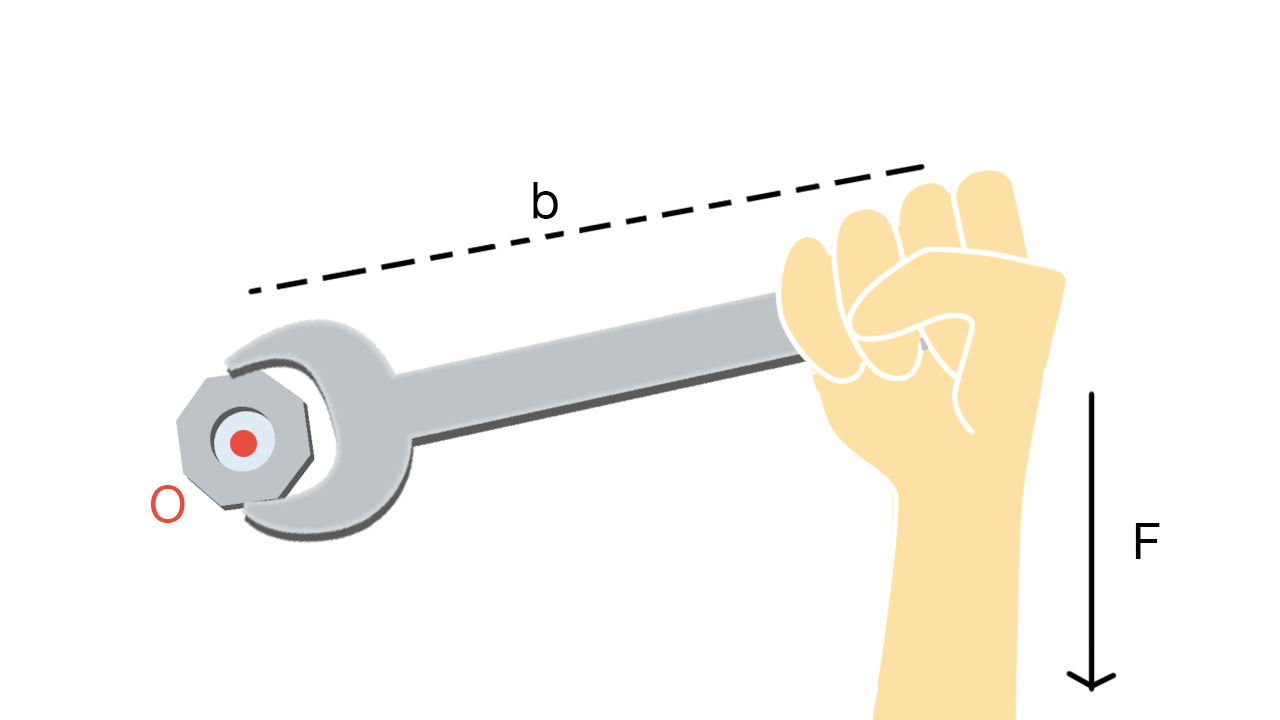
Perché per stringere i bulloni usiamo la chiave inglese? Perché l’effetto della rotazione è direttamente proporzionale non solo alla forza, ma anche al braccio.
Il braccio di una forza rispetto ad un punto £$O$£ è la distanza tra il punto £$O$£ e la retta che contiene il vettore £$\vec{F}$£.
Questo effetto di rotazione è un vettore e si chiama momento di una forza (£$\vec{M}$£) e si misura in £${N \ \cdot \ m}$£. Il momento di una forza è un vettore che ha:
- direzione perpendicolare al piano di rotazione
- verso uscente dal piano se il senso di rotazione è antiorario, entrante se è orario
- modulo equivalente al prodotto tra la Forza (£$\vec{F}$£), il braccio e il il seno dell’angolo compreso tra i due vettori.
Questo tipo di prodotto si chiama prodotto vettoriale. Se £$\theta$£, l’angolo compreso tra la forza e il braccio, sarà di 90° allora si otterrà l’effetto maggiore.
La formula si può riassumere in: £$M = F \cdot \ b \cdot \sin{\theta}$£
Il momento è direttamente proporzionale al raggio, quindi, per avvitare un bullone, se la chiave inglese è più corta occorre applicare più forza!
Esempio.
Se per avvitare un bullone uso una chiave inglese lunga £$0,2 \ \text{m}$£ e applico una forza perpendicolare ad essa di £$10 \ \text{N}$£:
£$M = F \cdot b \cdot \sin{90°} = $£ £$ 10 \ \text{N} \cdot 0,2 \ \text{m} \cdot 1 = $£ £$ 2 \ \text{N} \cdot \text{m}$£
Momento di una coppia di forze nell’equilibrio dei solidi
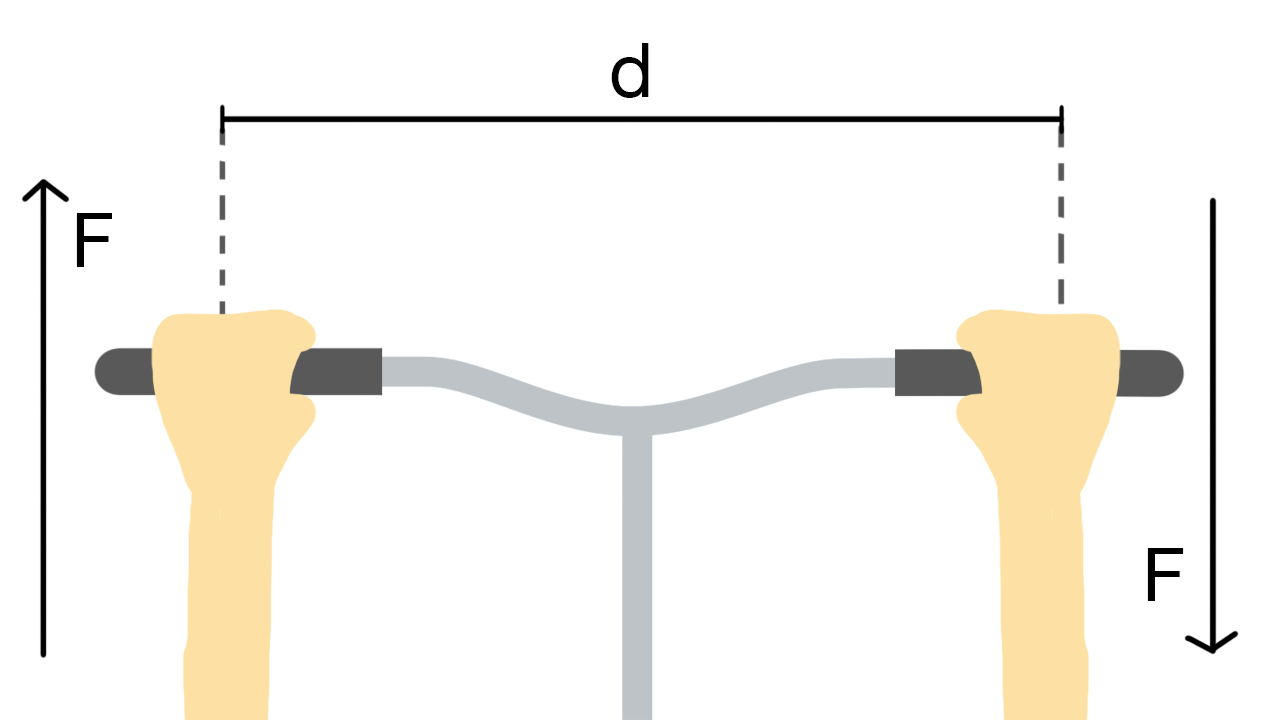
Nel manubrio di una bicicletta il momento è dato da una coppia di forze parallele e con lo stesso modulo che agiscono su due bracci adiacenti e della stessa lunghezza. In questo caso il momento è dato dalla somma di due momenti uguali e quindi il doppio di un singolo momento.
Questo momento si chiama momento di una coppia (£$M_c$£).
£$M_{c} = 2 \cdot F \cdot b = F \cdot d$£
dove £$d$£ è uguale alla distanza delle due rette parallele sulle quali giacciono i vettori Forza.
Equilibrio di un solido su un piano inclinato
Quando un corpo è appoggiato su un piano inclinato su di lui agiscono tre forze:
- la forza peso (£$\vec{F_p}$£), che ha direzione perpendicolare al suolo e verso diretto verso il basso
- la forza vincolare (£$\vec{N}$£), che ha direzione perpendicolare al piano e verso uscente dal piano
- un’eventuale forza esterna equilibrante (£$\vec{F_e}$£).
Attenzione!
La forza peso agisce sul piano ma verso il basso, se il piano è inclinato essa si deve scomporre in due componenti:
- La componente parallela al piano (£$F_{//}$£), con direzione parallela al piano e verso rivolto verso la base
- La componente perpendicolare al piano (£$F_⊥$£), con direzione perpendicolare al piano e verso rivolto verso il basso.
Modulo delle componenti della forza peso per l’equilibrio dei solidi
Il modulo della componente parallela al piano si trova moltiplicando la forza peso per il seno dell’angolo £$\alpha$£ compreso tra la base e la lunghezza del piano (ipotenusa).
Il seno dell’angolo £$\alpha$£ può essere trovato anche dividendo il cateto opposto all’angolo (£$h$£) e l’ipotenusa (£$l$£).
£$F_{//} = F_p \cdot \text{sen}{\alpha}$£ £$F_{//} = F_p \cdot \frac{h}{l}$£
Questo perché il triangolo formato dalla forza peso e dalle sue componenti è simile al triangolo £$A \stackrel\triangle{B} C$£ del piano inclinato.
Il modulo della componente perpendicolare della forza peso, invece, rappresenta l’altro cateto del triangolo rettangolo, quindi si può trovare moltiplicando la forza peso per il coseno dell’angolo £$\alpha$£.
£$F_⊥ = F_p \cdot \text{cos}{\alpha}$£ £$F_{⊥} = F_p \cdot \frac{b}{l}$£
Dove £$b$£ è la base del piano inclinato.
Come mettere in equilibrio un solido su un piano inclinato
Su un piano inclinato potrebbe agire una forza d’attrito radente statico (£$F_a$£) non trascurabile, che ha direzione parallela al piano e verso rivolto verso l’alto.
Il modulo massimo di questa forza si ricava dal prodotto tra la componente perpendicolare della forza peso e il coefficiente di attrito radente statico:
£$F_a = F_p \cdot \cos{\alpha} \cdot \mu_s$£
Alla forza d’attrito è opposta la componente parallela della forza peso, la quale agisce per spingere il corpo verso il basso. Se la forza d’attrito di distacco (£$F_p \cdot \cos{\alpha} \cdot \mu_s$£) è maggiore della componente parallela alla forza peso, il corpo resterà in equilibrio, viceversa se quest’ultima forza è maggiore, allora il corpo si muoverà verso il basso spinto da una forza risultante £$\vec{R}$£ che si ricava grazie alla differenza dei vettori £$\vec{F_a}$£ e £$\vec{F_{//}}$£.
Quando £$R$£ è diversa da [iol_placeholder type="formula" engine="katex" display="inline"/] per mantenere il corpo in equilibrio è necessario imprimergli una forza con lo stesso modulo e la stessa direzione ma verso opposto, quindi verso l’alto.
Esempio.
Se un armadio ha massa uguale a £$200 \ \text{kg}$£ ed è posizionato sopra un piano inclinato di £$30°$£, con un coefficiente d’attrito statico di £$\mu_s$£ di £$0,2$£ dovremmo applicare una forza di £$641\ \text{N}$£ per tenerlo in equilibrio poiché £$F_{//} = 980 \ \text{N} $£, £$F_a = 339 \ \text{N}$£ e £$\vec{R} = F_{//} – F_a$£
