Caricamento in corso...
Il lavoro termodinamico
Scopri cos’è il lavoro termodinamico e come si calcola nelle trasformazioni che abbiamo visto.
Appunti
Il lavoro termodinamico è molto importante per determinare alcune caratteristiche del sistema termodinamico in esame. Si calcola in maniera diversa a seconda della trasformazione presa in considerazione, inoltre, a differenza dell’energia interna, non è una funzione di stato.
Contenuti di questa lezione su: Il lavoro termodinamico
Il lavoro in una trasformazione isobara
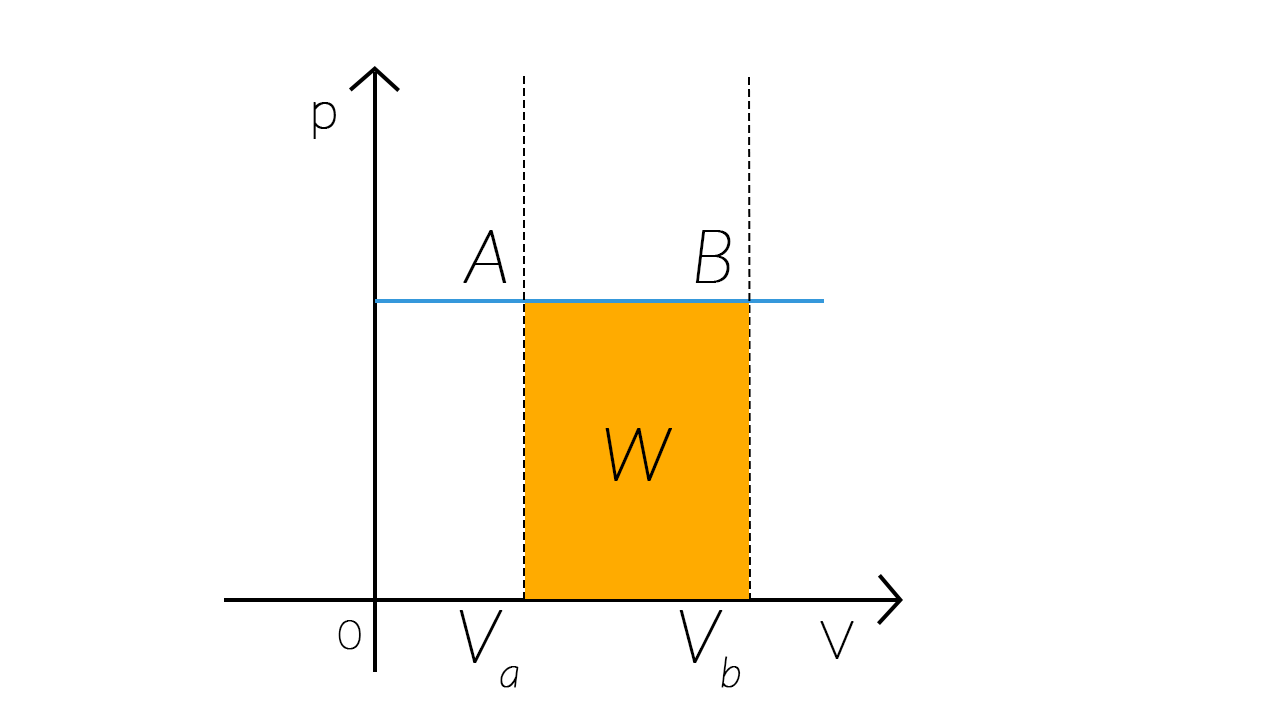
Per comprendere come varia il lavoro in una trasformazione isobara prendiamo ancora una volta il nostro cilindro (contenente del gas perfetto, riscaldato da una fiamma posta al di sotto e con un pistone che lo chiude).
Scaldiamo lentamente il gas contenuto nel cilindro, in modo che si espanda a pressione costante e lasciamo che il volume del gas aumenti in maniera quasistatica. Poiché il pistone si solleva, il sistema compie un lavoro positivo.
Pensa: si potrebbe utilizzare questo meccanismo per sollevare un oggetto tramite una carrucola.
Da un punto di vista quantitativo, il lavoro £$W$£ che il sistema compie, è uguale al prodotto tra la forza £$F$£, che spinge verso l’alto il pistone, e lo spostamento £$h$£ del pistone:
£$W=F\cdot h$£
Poiché la forza è uguale al prodotto della pressione £$p$£ del gas per la superficie £$S$£ del pistone, si ha:
£$W=F\cdot h=(p\cdot S)\cdot h=p\cdot(S\cdot h)=p\cdot \Delta V$£
dove £$\Delta V$£, uguale al prodotto £$Sh$£, è l’aumento di volume del gas.
Quindi il lavoro compiuto dal sistema a pressione costante è:
£$W=p\cdot \Delta V$£
Da questa considerazione si può dedurre che, in una qualsiasi trasformazione, il lavoro sia uguale all’area del rettangolo compreso tra l’asse dei volumi e il grafico della trasformazione in esame.
Il lavoro in una trasformazione isocora
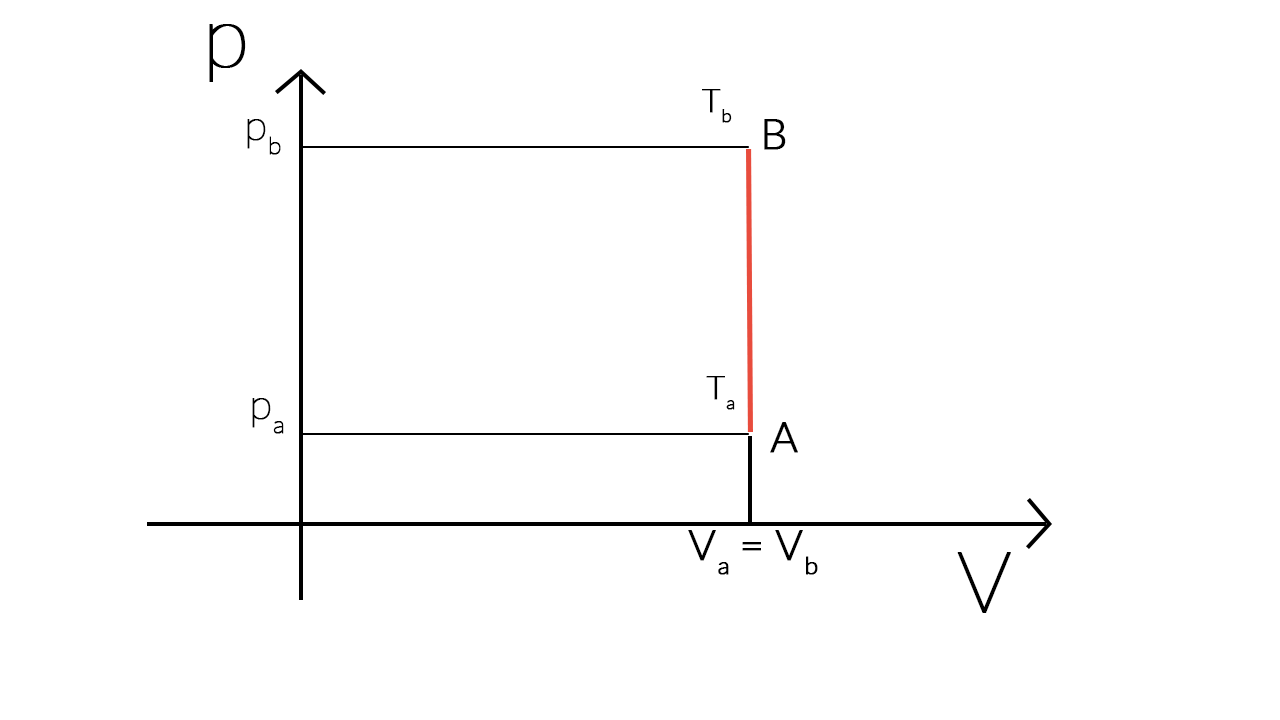
Ora che conosci le caratteristiche di una trasformazione isocora, calcolare il lavoro in una trasformazione di questo tipo ti risulterà molto facile. Infatti, essendo il lavoro pari all’area sottostante al grafico della trasformazione, ed essendo il grafico in questione un segmento verticale, è intuitivo che nelle trasformazioni isocore:
£$W=0$£
Oltre a questo possiamo anche aggiungere che, sostituendo nella relazione:
£$W=p\cdot\Delta V$£
il valore di £$\Delta V$£ è nullo, quindi il lavoro è nullo.
Il lavoro in una trasformazione ciclica
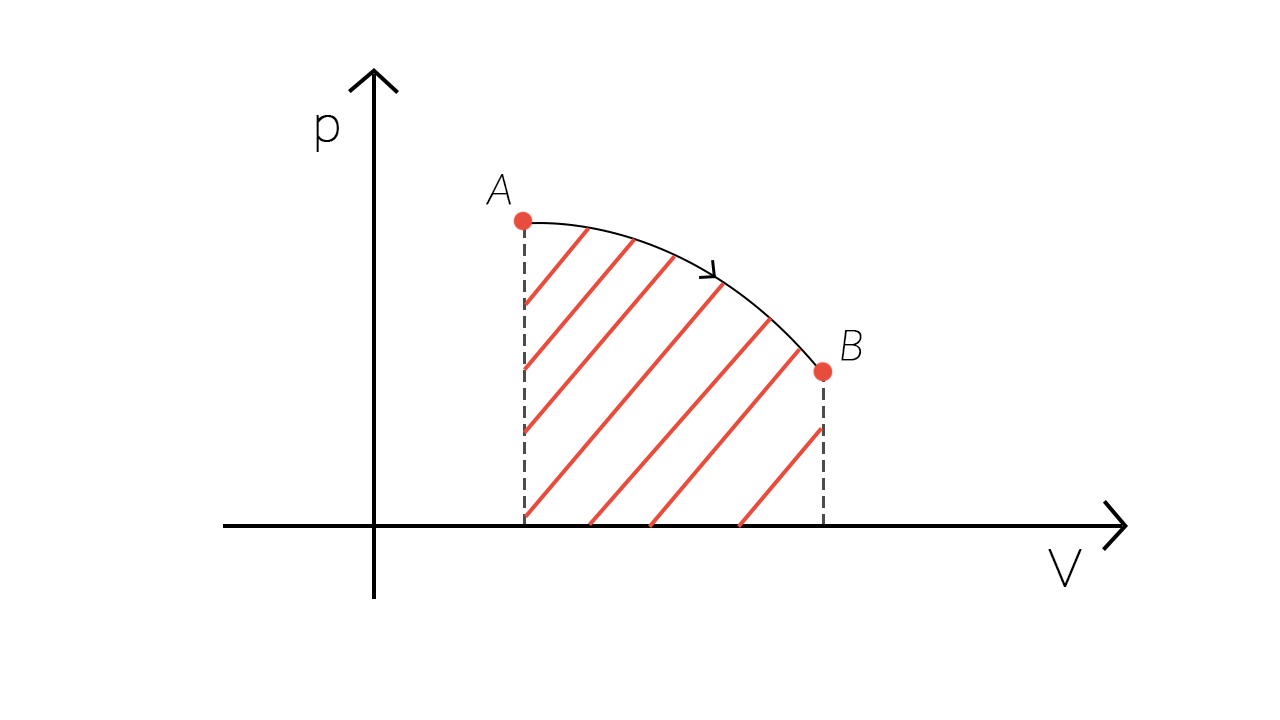
Espansione
Compressione
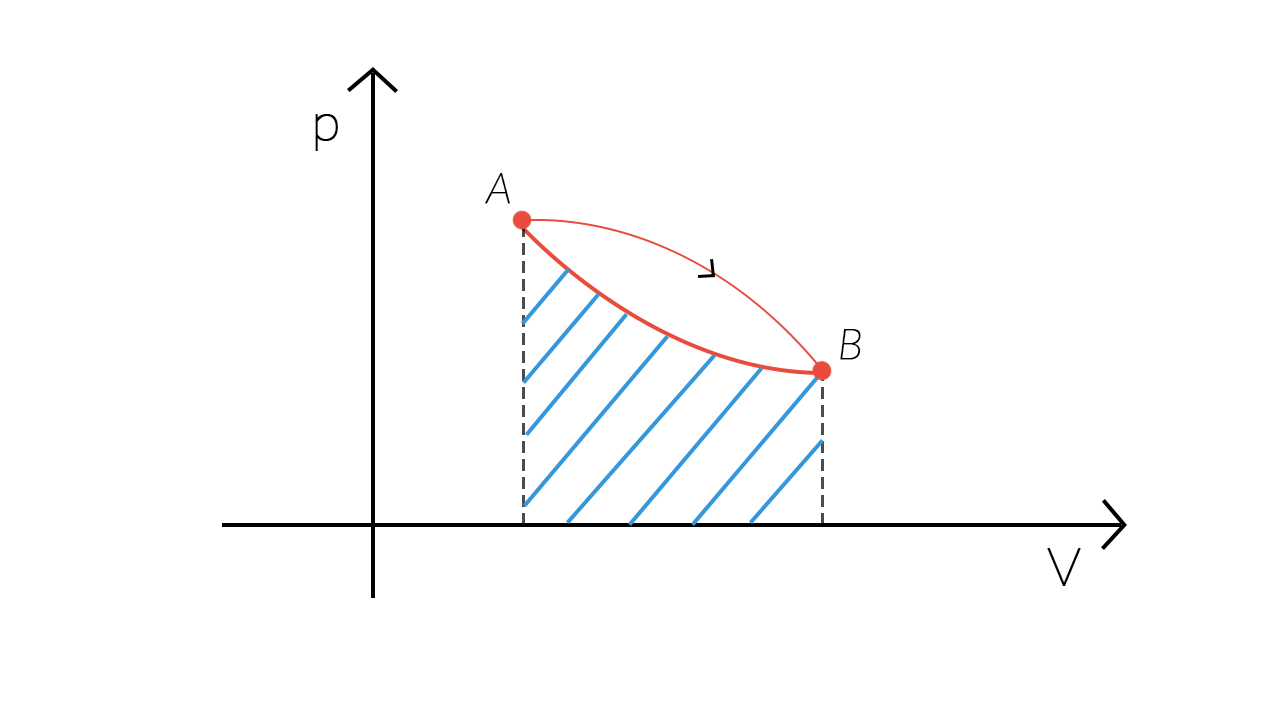
Trasformazione ciclica
Quando un gas si espande, durante una espansione, la variazione di volume £$\Delta V$£ è positiva, quindi il lavoro £$W$£ è positivo.
Durante una compressione, invece, la variazione di volume £$\Delta V$£ è negativa, e di conseguenza, il lavoro £$W$£ è negativo.
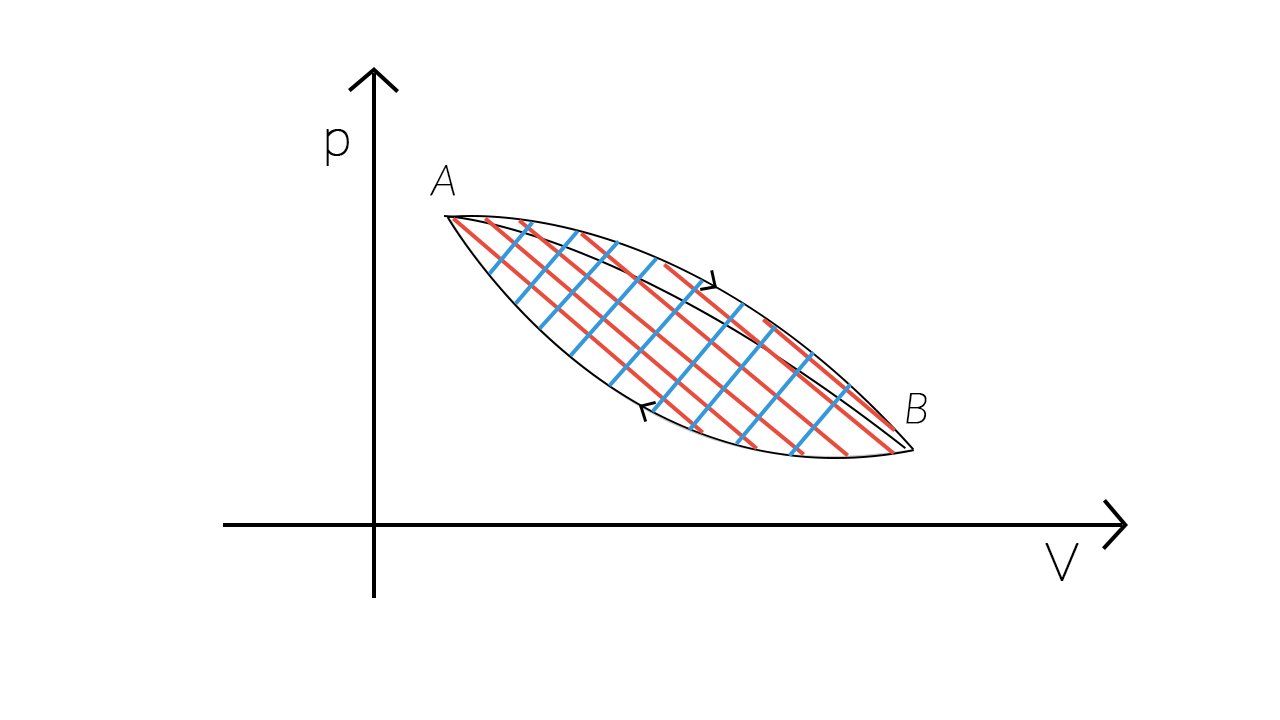
Durante una trasformazione ciclica del tipo mostrato nell’immagine ci sono una fase di espansione e una di compressione.
Durante la fase di espansione il sistema compie un lavoro positivo pari all’area della parte di piano tratteggiata in rosso.
Durante la fase di compressione il sistema compie un lavoro negativo, il cui valore assoluto è dato dall’area tratteggiata in grigio.
Il lavoro totale compiuto è uguale alla somma algebrica dei due lavori.
Il lavoro non è una funzione di stato
Esempio - Trasformazione 1
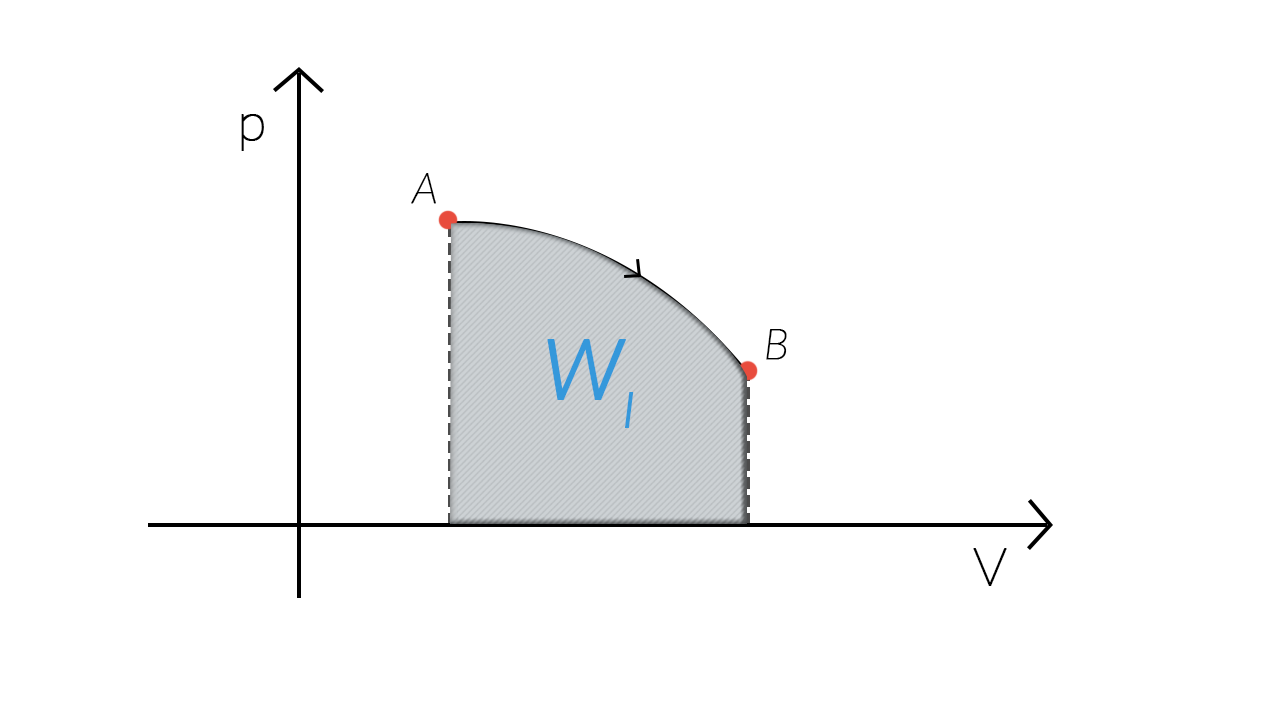
Esempio - Trasformazione 2
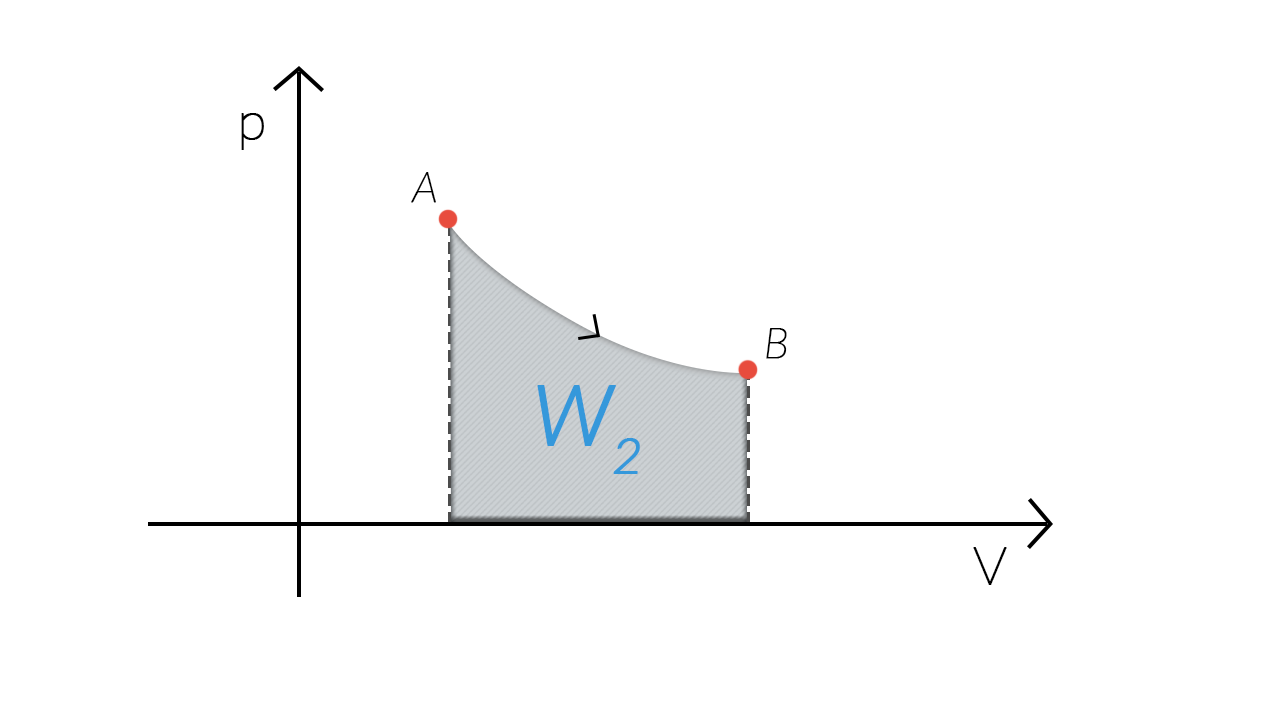
Consideriamo due trasformazioni quasistatiche che fanno passare un sistema dallo stesso stato iniziale £$A$£ allo stesso stato finale £$B$£ seguendo due percorsi diversi.
Il lavoro £$W_1$£ compiuto nella prima trasformazione è diverso dal lavoro £$W_2$£ compiuto nella seconda. Quindi il lavoro compiuto in una trasformazione non dipende soltanto dallo stato iniziale e da quello finale, ma anche dalla particolare trasformazione seguita nel passare da £$A$£ a £$B$£.
Quindi, al contrario dell’energia interna, il lavoro non è una funzione di stato.
