Il momento angolare e il momento d'inerzia
Il momento angolare, spesso sottovalutato nelle discussioni quotidiane sulla fisica, riveste un ruolo fondamentale nella descrizione e comprensione dei moti rotazionali. Si può immaginare come la “quantità di movimento” di un oggetto che ruota attorno a un punto, una sorta di controparte rotazionale della quantità di moto lineare.
In termini semplici, il momento angolare quantifica quanto velocemente e in che modo un corpo ruota attorno a un punto. Per un pianeta che orbita intorno al sole, per esempio, il momento angolare descrive la sua velocità e orientazione di rotazione.
Ma come si collega all’energia cinetica e al movimento? Bene, proprio come la quantità di moto lineare è legata all’energia cinetica di un oggetto in movimento rettilineo, il momento angolare è strettamente collegato all’energia cinetica rotazionale. Quando un oggetto ruota o orbita, possiede energia cinetica a causa di quel movimento. La relazione tra il momento angolare e questa energia è fondamentale per comprendere molti aspetti dei moti rotazionali, dai ghiaccioli che girano sul ghiaccio ai pianeti che orbitano attorno alle stelle.
Scopriamo insieme di più!
- Il momento angolare: la definizione
- La conservazione del momento angolare
- Il momento di inerzia
- Energia cinetica di un corpo rigido in rotazione
Il momento angolare: la definizione
Il momento angolare è una grandezza fisica vettoriale legata alle rotazioni spaziali: è la quantità che si conserva se un sistema fisico è invariante sotto rotazioni.
Costituisce l’equivalente per le rotazioni della quantità di moto per le traslazioni.
Nella meccanica newtoniana il momento angolare £$\vec {L}$£ di un punto materiale rispetto a un polo £$ \Omega $£ è definito come il prodotto vettoriale del vettore posizione £$\vec {r}$£ (con origine in £$\Omega$£ ) e del vettore quantità di moto £$\vec {Q}$£.
Omettendo la dipendenza dal polo:
£$\vec {L}=\vec {r}\times \vec {Q}=\vec {r}\times m\ \vec {v}$£
La conservazione del momento angolare
Il momento angolare è importante in tutti i moti dipendenti da variazioni che riguardano angoli.
Nei sistemi non soggetti a forze esterne, vale la legge di conservazione del momento angolare.
La conservazione del momento angolare è fondamentale nello studio dei moti dei pianeti e delle leggi di Keplero e nello studio del moto del pendolo.
Questa legge è conseguente alla seconda equazione cardinale:
£$ \frac{d\vec {L}}{dt}=\vec {M}_{tot} $£
in questa formula
- £$L$£ rappresenta il momento angolare del sistema
- £$\vec {L} = \vec {r} \times \vec {Q}$£ dove £$\vec {Q}$£ è la quantità di moto del sistema, applicata al centro di massa ed £$\vec {r}$£ è il vettore posizione del centro di massa rispetto all’asse di rotazione
- £$\vec {M}_{tot}$£ rappresenta il momento meccanico delle forze esterne £$\vec {F}_{tot}$£ (anch’esse applicate al baricentro)
- £$\vec {M}_{tot} = \vec {r} \times \vec {F}_{tot}$£
- Se tale momento è nullo, £$\vec {M}_{tot}=0$£ , risulta £$ \frac{d\vec {L}}{dt}=0 $£
Questo significa che £$L$£ è una costante del moto, ovvero che si conserva.
Il momento delle forze esterne può essere nullo (e quindi il momento angolare è costante) in questi tre casi:
- la forza esterna è nulla (il sistema è meccanicamente isolato)
- la forza è applicata in un punto dell’asse di rotazione (per cui £$r =0$£)
- la forza è diretta verso l’asse di rotazione, per cui £$\vec {F}$£ è parallelo ad £$\vec {r}$£, ovvero il loro prodotto vettoriale è nullo.
Esempio.
Una ruota di bicicletta in rotazione, se gli attriti sono trascurabili, tende a ruotare con la stessa frequenza e sullo stesso piano.
Il momento di inerzia
Per inerzia si intende la capacità dei corpi di opporsi ad una variazione del loro stato di quiete o moto.
Nel caso di moto di traslazione di un punto materiale, l’inerzia è rappresentata dalla massa. Nel caso, invece, della rotazione di un corpo rigido o di un punto materiale, l’inerzia è data dal momento d’inerzia, che dipende non solo dalla massa, ma anche dalla sua distribuzione attorno al punto (o all’asse) di rotazione.
Nel caso di un punto materiale (il caso più semplice), il momento di inerzia è £$I=mr^2$£. È una grandezza scalare che ha come unità di misura £$\text{kg}\cdot(\text{m}^2)$£.
Maggiore è il momento di inerzia, maggiore è la forza necessaria per variare la velocità di rotazione del corpo.
Per aumentare il momento di inerzia si può aumentare la massa e/o la distanza dall’asse, ponendo attenzione che al raddoppiare della distanza il momento quadruplica, perché il momento d’inerzia è direttamente proporzionale alla massa e direttamente proporzionale al quadrato della distanza.
Attenzione!
Il momento di inerzia può variare a seconda dell’asse di rotazione scelto attorno al quale si ruota. Bisogna quindi capire a quale asse riferirsi durante gli esercizi!
Il momento di inerzia può essere ricavato anche dal rapporto tra il modulo del momento angolare £$L$£ e quello della velocità angolare £$\omega$£: £$I = \frac{L}{\omega}$£.
Quindi, se il momento angolare è costante nel moto, momento di inerzia e velocità angolare sono inversamente proporzionali.
Esempio.
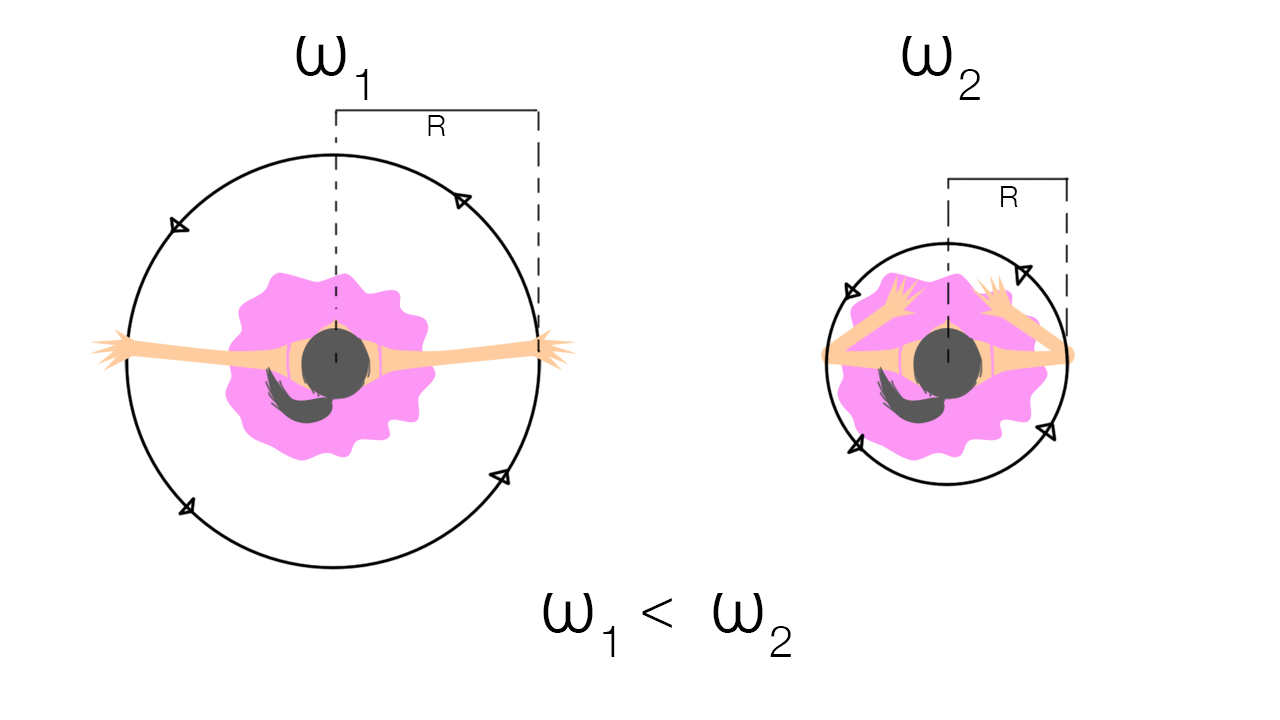
Se una ballerina fa una piroetta e allarga tutto ad un tratto le braccia o le gambe, la sua velocità angolare diminuisce poiché aumentando il raggio (braccia) aumenta anche il momento d’inerzia.
Energia cinetica di un corpo rigido in rotazione
L’energia cinetica associata al moto di rotazione di un corpo rigido viene anche detta energia rotazionale.
Nel caso di un corpo rigido a simmetria assiale e che ruoti attorno all’asse di simmetria, l’energia rotazionale risulta proporzionale al prodotto del momento di inerzia £$I$£ del corpo per il quadrato della sua velocità angolare £$\omega$£:
£$E={\frac {1}{2}}I\omega ^{2}$£
Attenzione!
L’espressione ricorda quella dell’energia cinetica, £$E={\frac {1}{2}}mv^{2}$£ ma:
- al posto della massa £$m$£ c’è il momento di inerzia e
- al posto della velocità lineare £$v$£ c’è la velocità angolare.
Nel caso in cui si parli di un oggetto puntiforme che ruota a distanza r dal centro di rotazione con una velocità angolare £$\omega$£, sostituendo £$I=mr^2$£ e £$\omega={\frac {v}{r}}$£…
Moti di traslazione e rotazione a confronto
Moto di traslazione:
Un corpo rigido trasla se tutti i suoi punti si spostano ad una distanza fissa nella stessa direzione.
L’orientamento del corpo nello spazio rimane lo stesso.
Un corpo può traslare se ha una velocità propria £$v$£, oppure se mosso da una o più forze.
Moto di rotazione:
Una rotazione è il movimento di un corpo che segue una traiettoria circolare.
In due dimensioni, cioè sul piano, una figura può ruotare attorno ad un punto detto centro di rotazione; in tre dimensioni, la rotazione avviene intorno ad una retta detta asse di rotazione.
Un corpo rigido ruota se ha una velocità di rotazione propria £$\omega$£, oppure se spinto a ruotare da una o più forze.
