I postulati di Einstein: enunciato e conseguenze

Il XX secolo ha rappresentato un periodo di profonde riformulazioni nel campo della fisica e uno dei protagonisti indiscussi di questa rivoluzione scientifica è stato Albert Einstein. Con le sue teorie sulla relatività, Einstein non solo ha rivoluzionato il modo in cui comprendiamo lo spazio, il tempo e l’energia, ma ha anche gettato le basi per gran parte della fisica moderna, influenzando discipline che vanno dalla cosmologia alla fisica delle particelle.

Alla base della teoria della relatività ristretta, pubblicata nel 1905, ci sono due postulati fondamentali: il primo sostiene che le leggi della fisica sono le stesse in tutti i sistemi di riferimento inerziali, cioè non accelerati; il secondo, forse ancora più rivoluzionario, afferma che la velocità della luce nel vuoto è sempre la stessa, indipendentemente dal movimento della sorgente luminosa o dell’osservatore.

Ma come è giunto Einstein a tali conclusioni? Le radici dei suoi postulati possono essere rintracciate in una serie di esperimenti e osservazioni sperimentali, in particolare l’esperimento Michelson-Morley, che aveva cercato senza successo di rilevare l’effetto del moto della Terra attraverso l’etere, il presunto mezzo attraverso il quale la luce si propagava. La mancanza di tale effetto pose un dilemma che le teorie fisiche dell’epoca non potevano spiegare. Invece di accettare l’idea dell’etere, Einstein ha proposto una soluzione audace: rifiutare il concetto di etere e riformulare completamente la nostra comprensione di spazio e tempo, attraverso formule complesse ma estremamente affascinanti.

Questi postulati hanno dato origine a una serie di predizioni e conclusioni, tra cui l’equivalenza tra massa ed energia, espressa dalla celebre equazione £$E=mc^2$£.

Scopriamoli insieme!

• Il primo postulato di Einstein
• Il secondo postulato di Einstein
• Il concetto di perdita del tempo assoluto per i postulati di Einstein

Il primo postulato di Einstein

Il primo postulato, chiamato principio della relatività ristretta (da non confondere con quello della relatività generale), afferma che le leggi e i principi della fisica hanno la stessa forma in qualsiasi sistema di riferimento inerziale. Questa ipotesi, già valida nella relatività galileiana, può sembrare scontata e banale, ma racchiude in sé molte conseguenze che hanno cambiato il modo di vedere il mondo. La prima di queste è la non esistenza dell’etere, sostanza che ai tempi si pensava fosse dispersa in tutto l’universo. Questa sostanza, trascinata dal moto di rotazione terrestre, avrebbe reso gli esperimenti sulla meccanica della luce condotti sulla terra inutili. La seconda osservazione da fare è che questo principio non viola la relatività galileiana, ma la conferma. Infatti la relatività ristretta non è una negazione di ciò che è stato affermato da Galilei, ma un superamento, una correzione per poter spiegare il comportamento dei corpi ad alte velocità e per poter introdurre i principi già pubblicati da Maxwell dell’elettromagnetismo.

Il secondo postulato di Einstein

Il secondo postulato, chiamato anche principio di invarianza della velocità della luce, afferma che la luce si muove nel vuoto a velocità costante (circa £$3 \cdot 10^8$£ £$\frac{m}{s}$£) in tutti i sistemi di riferimento inerziali, indipendentemente dal moto del sistema stesso o della sorgente da cui la luce è emessa. Questo postulato colpisce le fondamenta della relatività galileiana, per cui la velocità di un corpo non è costante, ma dipende dalla velocità di chi lo osserva. Per la luce non è così, infatti, se osserviamo la luce nel vuoto, questa si muoverà sempre alla stessa velocità (per saperne di più va a ELETTROMAGNETISMO (link)). La velocità della luce è infatti una costante che viene chiamata £$c$£. La prima importantissima conseguenza di questo postulato è che £$c$£ non solo è costante, ma è la massima velocità universale, nessun corpo dotato di massa può raggiungerla o anche solo avvicinarvisi.

Il concetto di perdita del tempo assoluto per i postulati di Einstein

Proviamo ora a risolvere un piccolo problema utilizzando ciò che abbiamo imparato nella relatività galileiana ed applicando i due postulati.

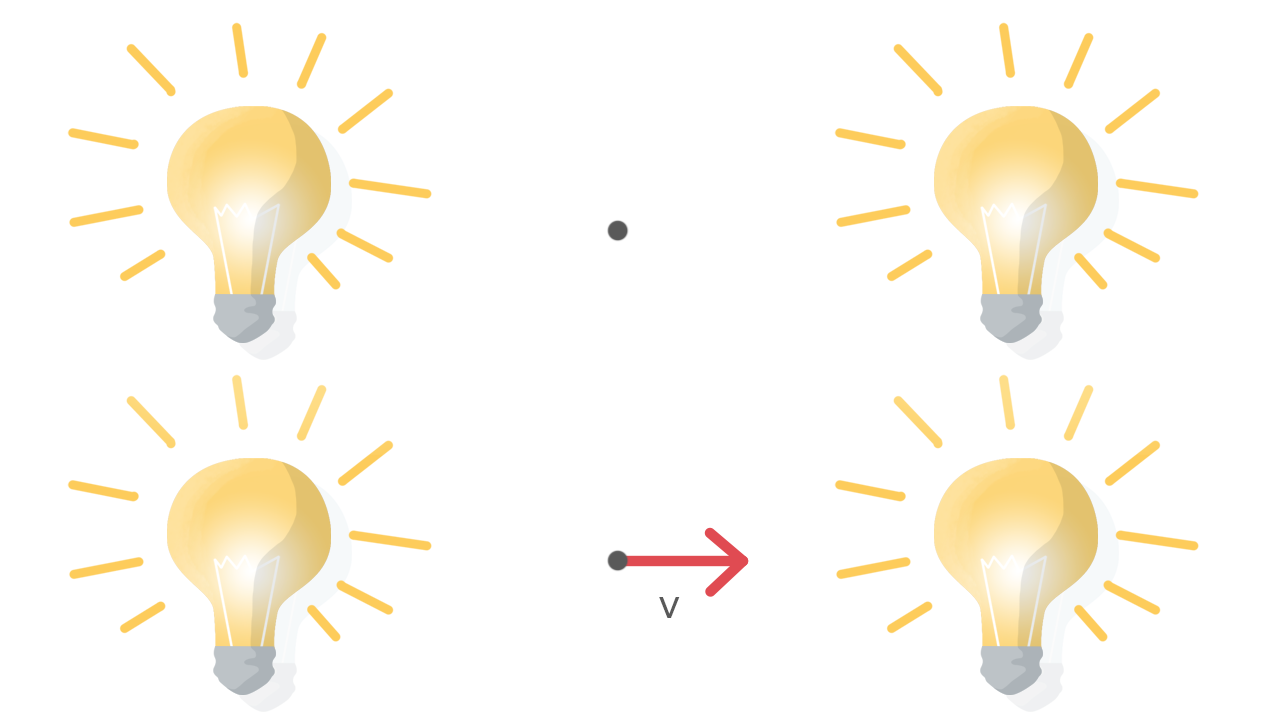
Un osservatore vede due lampadine ferme ed equidistanti accendersi insieme. Facilmente ne deduce che, perché la luce delle due lampadine arrivi a lui contemporaneamente, le due lampadine si devono essere accese simultaneamente. In relatività galileiana questo risultato sarebbe assoluto, le lampadine si sono accese nello stesso momento per chiunque.

Poniamo ora un secondo osservatore, nella stessa posizione del primo, ma con velocità £$v$£ verso una delle due lampadine. L’osservatore vedrà una lampadina accendersi prima dell’altra, infatti nel tempo che la luce impiega ad arrivare a lui, egli non sarà più nel mezzo e vedrà prima accendersi la lampadina verso cui si sta spostando.

Svolgendo i calcoli classici troveremmo ancora che le due lampadine si sono accese contemporaneamente, ma applicando il secondo principio (£$c+v=c$£ e £$c-v=c$£ dal momento che la velocità della luce nel vuoto è costante) i calcoli non tornano e risulterebbe che le due lampadine non si sono accese nello stesso momento.

Questo problema ci mostra come nella relatività ristretta il tempo non sia assoluto, ma anch’esso dipenda dal sistema di riferimento. Dalla perdita di questa invariante nasce la necessità di un nuovo sistema per svolgere i calcoli, chiamato trasformazioni di Lorentz. E’ importante ricordare che questo “esperimento” mette in crisi anche il concetto classico di simultaneità.

La simultaneità diventa così un concetto relativo perché ciò che è simultaneo per un sistema di riferimento potrebbe non esserlo per un altro.