Il principio di Archimede e il rapporto con la forza peso

In questa lezione imparerai a capire come la capacità di un corpo di restare a galla sia determinata da un bilancio di forze. Comprenderai come ogni corpo cerchi di stabilire una situazione di equilibrio, posizionandosi ad una determinata quota all’interno del fluido in cui è immerso. Scoprirai inoltre come stabilire a priori se un determinato corpo sarà in grado di galleggiare o affonderà nel fluido in cui viene immerso.

Il principio di Archimede descrive il comportamento di un corpo all’interno di un fluido, prevedendone la sua capacità a galleggiare o affondare. Per poter stabilire la posizione esatta che quest’ultimo assumerà all’interno del fluido è però necessario conoscerne il peso e, solo dopo, confrontare quest’ultimo con la spinta di Archimede ricevuta dal fluido. Scopriamolo insieme!

• La storia del principio di Archimede: come è stato scoperto
• La forza peso nel principio di Archimede
• Galleggiamento o affondamento: il principio di Archimede
• Bilancio di forze nel principio di Archimede
• Prevedere se un corpo galleggerà in acqua secondo il principio di Archimede

La storia del principio di Archimede: come è stato scoperto

Il principio di Archimede è uno dei concetti fondamentali che governano il comportamento dei fluidi, e il suo impatto si estende a molteplici domini, dalla scienza alla tecnologia e all’ingegneria. Nominato in onore del grande matematico e fisico greco Archimede di Siracusa, questo principio stabilisce che un corpo immerso in un fluido sperimenta una forza verso l’alto, chiamata spinta, pari al peso del fluido spostato dal corpo. In altre parole, la spinta su un oggetto sommerso è uguale al peso del liquido che l’oggetto sposta.

La storia racconta che Archimede scoprì questo principio mentre faceva il bagno nella sua vasca. Notò che l’acqua traboccava dalla vasca quando lui vi entrava, e questo lo portò a riflettere sul rapporto tra il volume dell’acqua spostata e il volume del suo corpo immerso. La leggenda vuole che fosse così entusiasta della sua scoperta da saltare fuori dalla vasca e correre nudo per le strade di Siracusa esclamando “Eureka!” (Ho trovato!).

Ma fu l’applicazione pratica di questa scoperta che fece guadagnare ad Archimede il riconoscimento eterno. Il re di Siracusa gli chiese di verificare se una corona d’oro che aveva ordinato fosse stata realizzata con oro puro o se l’artigiano avesse sostituito parte dell’oro con un metallo meno prezioso. Archimede risolse il problema immergendo la corona in un recipiente colmo d’acqua e misurando il volume di liquido spostato, confrontandolo poi con il volume di un pezzo d’oro dello stesso peso. In questo modo, poté determinare se la densità della corona corrispondesse a quella dell’oro puro.

Nel nostro articolo, esploreremo in profondità il principio di Archimede, i dettagli del suo esperimento storico e l’impatto duraturo di questa scoperta sulla scienza e sulla tecnologia. Analizzeremo come il principio venga utilizzato in contesti moderni, come la progettazione di navi e sottomarini, e come continui ad essere un elemento fondamentale nella comprensione dei fluidi.

La forza peso nel principio di Archimede

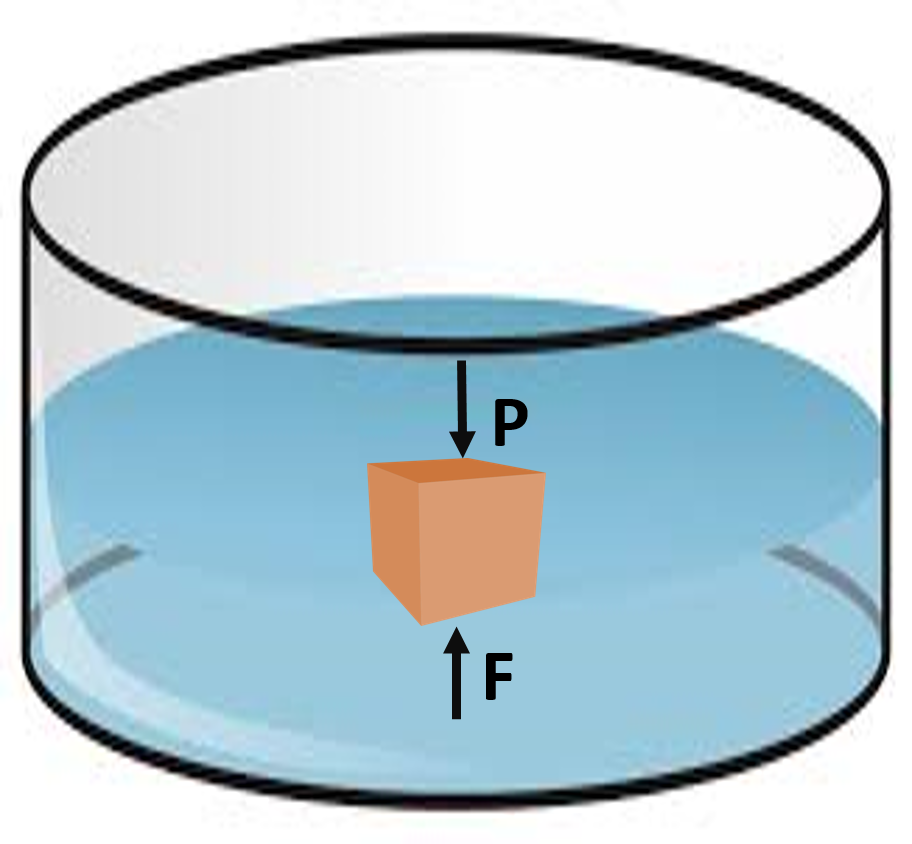
Il principio di Archimede ci permette di calcolare la spinta ricevuta da un qualsiasi corpo immerso in un fluido, di conseguenza potremmo essere in grado di valutare se un corpo sarà in grado di galleggiare o meno. Immaginiamo di avere un corpo immerso in acqua e di valutare tutte le forze che insistono su di esso. Oltre alla spinta di Archimede diretta verso l’alto, vi sarà la forza peso del corpo stesso che tenderà a portarlo verso il basso.

È intuitivo pensare che il corpo sarà in grado di galleggiare se la spinta di Archimede sarà grande a sufficienza da battere la forza peso del corpo, mentre affonderà quando il suo peso sarà tale da non venire contrastato a sufficienza dalla forza esercitata dal fluido su di esso. Per poter fare questo confronto matematico si compareranno i due valori seguenti:

£$F = \varrho_{f}\cdot V_{imm}\cdot g$£

e

£$P = \varrho_{s}\cdot V_{tot}\cdot g$£

Dove:

• £$F$£ è la forza esercitata del fluido, nota come spinta di Archimede, in £$[N]$£, già analizzata in precedenza
• £$P$£ è la forza peso del corpo, in £$[N]$£. Essa potrebbe essere nota a priori, oppure potrebbe essere calcolata noti i dati riportati di seguito
• £$\varrho_{f}$£ è la densità del fluido, in £$[kg/m^3]$£
• £$\varrho_{s}$£ è la densità del solido immerso, in £$[kg/m^3]$£
• £$V_{imm}$£ è il volume del solido immerso, in £$[m^3]$£
• £$V_{tot}$£ è il volume totale di corpo, non sono la parte immersa, in £$[m^3]$£
• £$g$£ è l’accelerazione di gravità, in £$[m/s^2]$£

Galleggiamento o affondamento: il principio di Archimede

Il confronto tra la spinta di Archimede e la forza peso del corpo immerso ci può portare a capire se un corpo galleggerà o affonderà in un fluido.

Immaginiamo di immergere un corpo in acqua ad una data profondità e di mantenerlo manualmente in quella posizione; quando lasceremo il corpo libero di muoversi potranno verificarsi quattro situazioni diverse:

• Caso A: Il corpo resta esattamente nella stessa posizione senza muoversi affatto
• Caso B: Il corpo risale leggermente trovando una situazione di equilibrio ad una quota più alta
• Caso C: Il corpo scende leggermente trovando una situazione di equilibrio ad una quota più bassa
• Caso D: Il corpo affonda del tutto fino ad appoggiarsi sul fondo del contenitore

Ciascuna delle situazioni qui elencate può essere matematicamente spiegata con il confronto tra la forza peso e la spinta di Archimede.

Nel Caso A il corpo non si muove affatto: questo significa che il volume immerso è tale da provocare una spinta di Archimede verso l’alto che sta eguagliando perfettamente la forza peso del corpo. Di conseguenza esso si trova già in una situazione di equilibrio.

Nel Caso B il corpo è posizionato da noi ad una quota tale per cui la parte di volume immerso sta determinando una spinta di Archimede superiore alla forza peso dello stesso. Come conseguenza, essa tenderà a far risalire leggermente il corpo. Quest’ultimo si fermerà ad una quota più alta in corrispondenza della quale il volume immerso determinerà una spinta di Archimede uguale alla forza peso, in una situazione di perfetto equilibrio.

Nel Caso C avremo una situazione analoga al caso precedente, ma invertita: il corpo è posizionato da noi ad una quota tale per cui la parte di volume immerso sta determinando una spinta di Archimede inferiore alla forza peso dello stesso. Come conseguenza, il peso tenderà a far scendere leggermente il corpo. Quest’ultimo si fermerà ad una quota più bassa in corrispondenza della quale il volume immerso determinerà una spinta di Archimede uguale alla forza peso, in una situazione di perfetto equilibrio.

Nel Caso D infine, avremo una forza peso nettamente superiore alla spinta di Archimede, di conseguenza il corpo tenderà ad affondare completamente nel fluido fino a toccare il fondo.

Bilancio di forze nel principio di Archimede

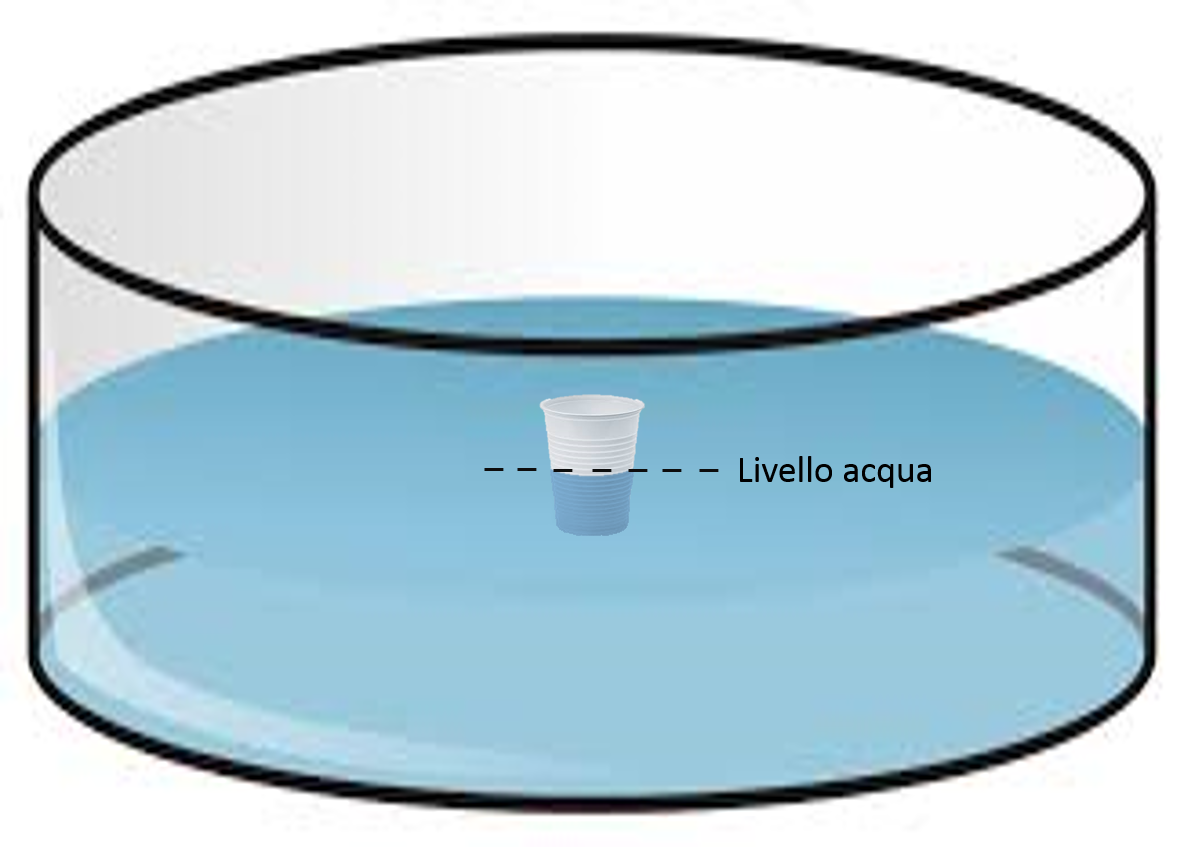
Abbiamo imparato come ogni corpo cerchi di posizionarsi in una situazione di equilibrio in cui la sua porzione di volume immerso sia in grado di provocare una spinta di Archimede tale da eguagliare la forza peso del corpo stesso. Riprendiamo quindi l’esperimento del bicchiere di plastica nella bacinella visto nella lezione precedente e proviamo a fare qualche considerazione in più.

Quando rilasciamo il bicchiere ed esso è in una situazione in cui la spinta di Archimede supera la forza peso, il bicchiere risalirà riducendo la porzione di volume immerso. Così facendo si starà automaticamente diminuendo anche il valore della spinta di Archimede, fino a portarla ad eguagliare la forza peso dell’intero bicchiere.

Nella situazione in cui invece, rilasciando il bicchiere, lo si lascia in una posizione in cui la spinta di Archimede non è abbastanza alta da eguagliare il peso, esso inizierà ad affondare. Il bicchiere in questione, o un corpo in generale, potrà essere in grado di trovare una nuova situazione di equilibrio se, avanzando lungo il basso ed incrementando in contemporanea la sua porzione di volume immerso, l’incremento di spinta di Archimede ottenuto sarà tale da eguagliare la forza peso. Per raggiungere tale equità potrebbe essere necessario che tutto il volume del corpo sia immerso, in tal caso saremmo in una situazione in cui la spinta di Archimede eguaglia il peso solo se tutto il corpo contribuisce al volume immerso. Potrebbe però accadere che, anche sfruttando l’intero volume di corpo a disposizione, la spinta di Archimede non sia sufficientemente alta da contrastarne il peso: in tal caso esso affonderà inesorabilmente verso il fondo.

In conclusione, un corpo affonderà sicuramente se la sua forza peso supera la massima spinta di Archimede ottenibile sfruttando tutto il volume del corpo £$V_{tot}$£ e sostituendolo al termine £$V_{imm}$£ nella formula classica della spinta di Archimede:

£$F_{max} = \varrho_{f}\cdot V_{}\cdot g$£

Un corpo potrà invece galleggiare se la massima spinta di Archimede è inferiore alla forza peso dello stesso. In tal caso infatti, esso si posizionerà in modo da raggiungere la situazione di equilibrio in cui:

£$F=P$£

Prevedere se un corpo galleggerà in acqua secondo il principio di Archimede

È possibile indovinare a priori se un corpo galleggerà in acqua? La risposta è si, e il motivo è molto semplice.

Dato un qualsiasi corpo, siamo sicuri che esso avrà modo di galleggiare se la sua densità è inferiore a quella del fluido in cui è immerso, poiché, data una certa porzione di volume immerso, la spinta di Archimede risultante eguaglierà già il peso del corpo.

Se la sua densità eguaglia quella del fluido in cui è immerso, il corpo si posizionerà a filo del pelo libero poiché l’equilibrio tra la forza peso del corpo e la spinta di Archimede sarà raggiunto quando il volume immerso eguaglierà il volume totale.

Da ultimo, un corpo affonderà sicuramente se la sua densità supera quella del fluido in cui è immerso poiché, anche utilizzando tutto il volume di corpo nell’espressione della spinta di Archimede, non si riuscirebbe a ricavare un valore di forza sufficientemente alto da contrastare il peso dell’oggetto.