Grandezze scalari e grandezze vettoriali: la differenza
La fisica, in quanto disciplina che esplora la natura e i suoi principi fondamentali, utilizza una vasta gamma di termini e concetti per descrivere il mondo intorno a noi. Tra questi, due concetti fondamentali sono le grandezze scalari e le grandezze vettoriali. Queste due categorie rappresentano non solo le basi della fisica classica, ma influenzano anche profondamente la nostra comprensione dei fenomeni complessi in fisica moderna e quantistica.
Nella vita di tutti i giorni, spesso inconsciamente, ci imbattiamo in esempi di entrambe le grandezze. Quando controlliamo la temperatura, stiamo considerando una grandezza scalare; mentre quando controlliamo la velocità e la direzione del vento, stiamo lavorando con una grandezza vettoriale. Queste distinzioni, apparentemente semplici, diventano di fondamentale importanza quando ci addentriamo in studi più avanzati, come la dinamica dei fluidi o la teoria della relatività.
Le grandezze scalari e vettoriali differiscono principalmente nella natura delle informazioni che trasmettono. Mentre le grandezze scalari forniscono un valore assoluto, come la massa o l’energia, le grandezze vettoriali offrono un quadro più completo, dando informazioni sia sulla magnitudine che sulla direzione, come nel caso della forza o della velocità. Questa distinzione diventa ancora più cruciale quando affrontiamo problemi che richiedono un’analisi vettoriale, come nel caso della meccanica dei corpi rigidi o degli studi sull’elettromagnetismo.
Scopriamole insieme!
- Il DNA dei dati fisici
- Com'è fatto un dato
- Cosa sono e a che cosa servono i vettori
- Definizione di direzione e verso ed esempi di grandezze scalari e vettoriali
- Come rappresentare geometricamente un vettore
- Cosa significa scomporre un vettore nelle sue componenti
- Come scomporre un vettore nelle sue componenti
- Vettori e quadranti
- Cosa sono i versori
- Dalle componenti al vettore
Il DNA dei dati fisici
Il DNA dei dati: come è fatto, dentro, un dato fisico?
Abbiamo visto come il fare una misura significa, per un fenomeno fisico, associare un numero a una unità di misura. Questo non ci basta: come sono fatti, davvero, questi dati?
Guardiamo all’interno del dato così come guarderemmo all’interno di un essere vivente per scoprire le informazioni fondamentali che lo definiscono, ossia il suo DNA. In fisica i dati hanno un loro proprio DNA, che non è composto da quattro basi azotate (A-T-C-G, adenina, timina, citosina, guanina) come per gli esseri viventi, ma da una, o da tre informazioni fondamentali:
- modulo
- direzione
- verso.
Esempio.
Prendiamo una grandezza fisica come il volume di una balenottera azzurra, l’animale più grande che si trova sul nostro pianeta. Il Volume è una grandezza fisica che, nel Sistema Internazionale, si misura in metri cubi.
Per misurare il Volume della balenottera, la immergiamo in una piscina d’acqua salata per la sua sicurezza e per la nostra facilità di misura: la balenottera si mantiene ferma perché, da animale intelligente, è a sua volta curiosa di conoscere il risultato.
Ipotizziamo che la piscina abbia la forma di un cubo il cui lato ci è noto e che sia quasi piena d’acqua; immergiamo completamente la balenottera, sempre ferma e collaborativa, osserviamo l’innalzamento del livello dell’acqua, ringraziamo Archimede e misuriamo il Volume dell’acqua dal livello precedente senza balena al nuovo livello con balena immersa. Otteniamo un Volume di, proviamoci, 230 £$m^3$£.
Ci serve sapere altro? No, la misura è completa: abbiamo una valore numerico, il modulo, pari a 230, e un’unità di misura, i £$m^3$£, e non occorre altro. Lo comunichiamo alla balena, che se ne compiace e che si offre di continuare a lavorare con noi, ma che chiede, giustamente, di essere liberata in mare aperto.
Liberiamo la balenottera in mare aperto, quindi ci poniamo la questione di valutare la sua velocità espressa, nel SI, in metri al secondo (£$\frac{m}{s}$£) e che può essere anche espressa in una delle sue unità di misura derivate e più comuni, come i kilometri all’ora (£$\frac{km}{h}$£).
Per osservare la velocità della balenottera, libera di muoversi nell’oceano, e per descriverla, non ci basta sapere a quanti km/h si stia muovendo, ossia non ci basta il modulo della velocità, ma occorre avere due informazioni aggiuntive:
- la direzione, ossia la linea retta immaginaria lungo la quale la balenottera si sta muovendo, istante per istante
- il verso, ossia sapere se la balenottera, lungo questa retta, sta andando in avanti o in retromarcia.
Associamo quindi, istante per istante, al modulo della velocità della balenottera la sua direzione e il suo verso, e indichiamo più propriamente la velocità con £$\vec{v}$£
Com’è fatto un dato
I dati non sono tutti uguali: ad alcuni basta solo un numero e un’unità di misura, altri invece hanno bisogno di qualcos’altro: direzione e verso!
Stiamo parlando degli scalari e dei vettori.
Scopriamo ora quali grandezze possono essere considerate scalari e quali vettoriali!
Il volume (£$V$£) è una grandezza scalare perché per definirlo basta solo un numero e un’unità di misura (£$m^3$£ o multipli e sottomultipli). Non c’è bisogno di stabilire altri dati.
La velocità (£$\vec{v}$£), invece, necessita un modulo, una direzione e un verso per essere definita. La velocità è una grandezza vettoriale.
Cosa sono e a che cosa servono i vettori
In fisica ci sono due tipi di grandezze:
- quelle che possono essere espresse semplicemente tramite un numero, riferito a un’unità di misura (ad esempio, la lunghezza, il tempo, la temperatura, l’energia)
- quelle per le quali un numero e un’unità di misura non bastano (ad esempio, lo spostamento, la velocità, l’accelerazione)
Le prime si dicono grandezze scalari, le seconde grandezze vettoriali. Per esprimere una grandezza vettoriale, cioè per descrivere un vettore, abbiamo bisogno di tre informazioni:
- un modulo (detto anche intensità), cioè l’informazione numerica rapportata a un’unità di misura
- una direzione
- un verso
Definizione di direzione e verso ed esempi di grandezze scalari e vettoriali
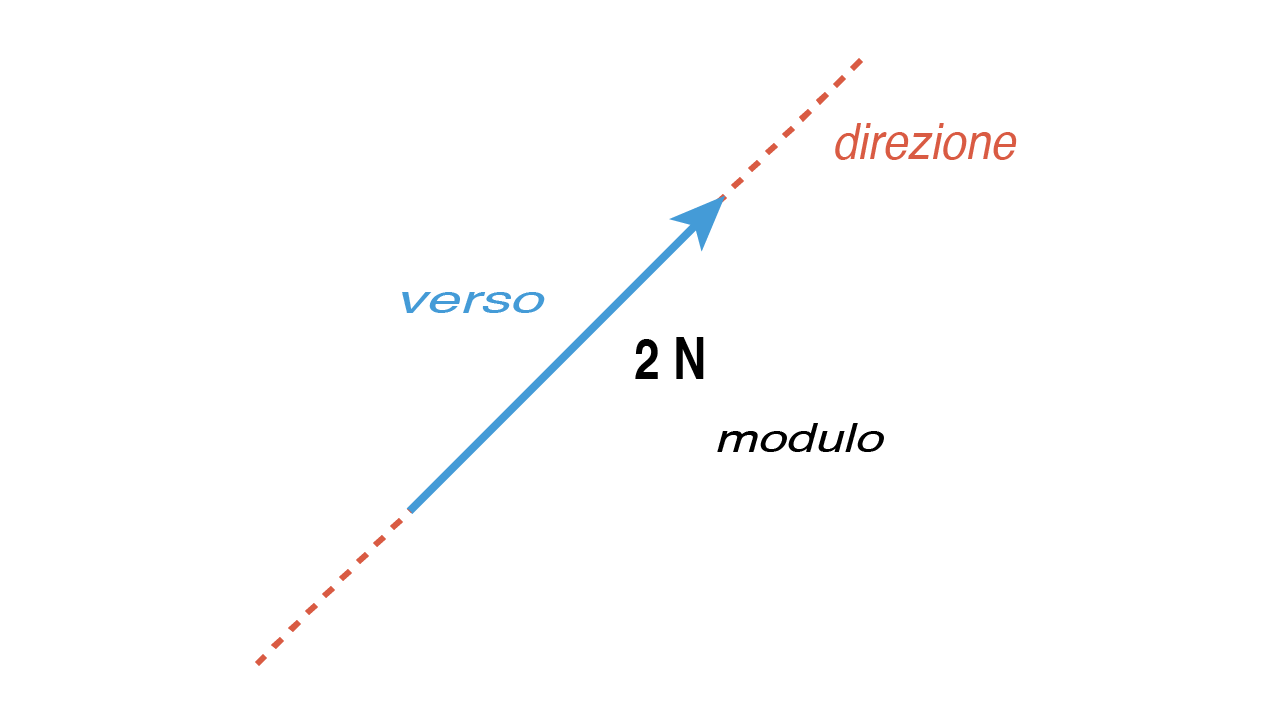
La direzione è il fascio improprio di rette a cui appartiene anche la retta lungo cui agisce il vettore.
Il verso è il senso verso il quale agisce il vettore.
Esempi di grandezze scalari:
- massa (£$m$£)
- temperatura (£$T$£)
- volume (£$V$£)
- densità (£$d$£)
- pressione (£$P$£)
Esempi di grandezze vettoriali:
- forza (£$\vec{F}$£)
- velocità (£$\vec{v}$£)
- accelerazione (£$\vec{a}$£)
- quantità di moto (£$\vec{p}$£)
- momento angolare (£$\vec{L}$£)
Attenzione!
Le informazioni di direzione e verso di una grandezza fisica uniscono le caratteristiche statiche di un corpo (il suo volume, ma anche la sua massa, la sua temperatura, la sua carica elettrica, tutte grandezze scalari), con le caratteristiche dinamiche di un corpo (la sua velocità, la sua accelerazione, la forza che imprime, grandezze vettoriali).
Il potere contagioso delle grandezze vettoriali!
In un’equazione fisica, la presenza di una grandezza vettoriale (es. la velocità espressa in termini di modulo direzione e verso) contagia le grandezze da essa derivate. In termini semplici, l’accelerazione è la variazione della velocità con il tempo ed è essa stessa una grandezza vettoriale, necessitando di informazioni dinamiche come direzione e verso.
Come rappresentare geometricamente un vettore
Per rappresentare geometricamente un vettore puoi disegnare un segmento orientato, cioè un segmento con una freccia. In questo modo:
- il modulo del vettore è indicato dalla lunghezza del segmento;
- la direzione del vettore corrisponde alla retta alla quale appartiene il segmento orientato, o a una qualsiasi altra retta parallela;
- il verso del vettore è indicato dalla punta della freccia.
I due punti estremi di un vettore non sono intercambiabili: uno è il “punto iniziale” e l’altro il “punto finale” del vettore. Puoi indicare un vettore con la scrittura £$\overrightarrow{AB}$£, oppure, in alternativa, usando una lettera, ad esempio con £$\overrightarrow{v}$£. Un altro modo frequente di indicare un vettore è utilizzare il grassetto: £$\mathbf{v}$£. Il vettore £$\overrightarrow{BA}$£ non è uguale al vettore £$\overrightarrow{AB}$£: questi due vettori hanno infatti uguale modulo (£$\overline{AB} = \overline{BA}$£), uguale direzione, ma versi opposti, e si dicono opposti tra di loro.
Cosa significa scomporre un vettore nelle sue componenti
Se tracci in un piano cartesiano le due rette passanti per gli estremi di un vettore £$\overrightarrow{v}$£ e perpendicolari agli assi, ottieni le proiezioni del vettore sui due assi. Le lunghezze di tali proiezioni sono dette componenti del vettore lungo gli assi cartesiani.
Altrimenti utilizzando la goniometria puoi trovare anche le componenti del vettore tramite il seno ed il coseno dell’angolo £$\alpha$£
Attenzione!: la componente del vettore lungo l’asse £$x$£ devi considerarla col segno negativo se il verso del vettore punta a sinistra; la componente lungo l’asse £$y$£ devi considerarla negativa se il verso del vettore punta in basso.
Applicando i teoremi della trigonometria e il teorema di Pitagora al triangolo rettangolo formato dal vettore £$\overrightarrow{v}$£ e dalle rette perpendicolari agli assi, puoi determinare:
- le componenti del vettore, dati il suo modulo e l’angolo £$\alpha$£ compreso tra la direzione del vettore e l’asse £$x$£;
- l’angolo £$\alpha$£, date le componenti del vettore;
- il modulo del vettore, date le sue componenti.
Di seguito scopriremo nel dettaglio come scomporre un vettore nelle sue componenti.
Come scomporre un vettore nelle sue componenti
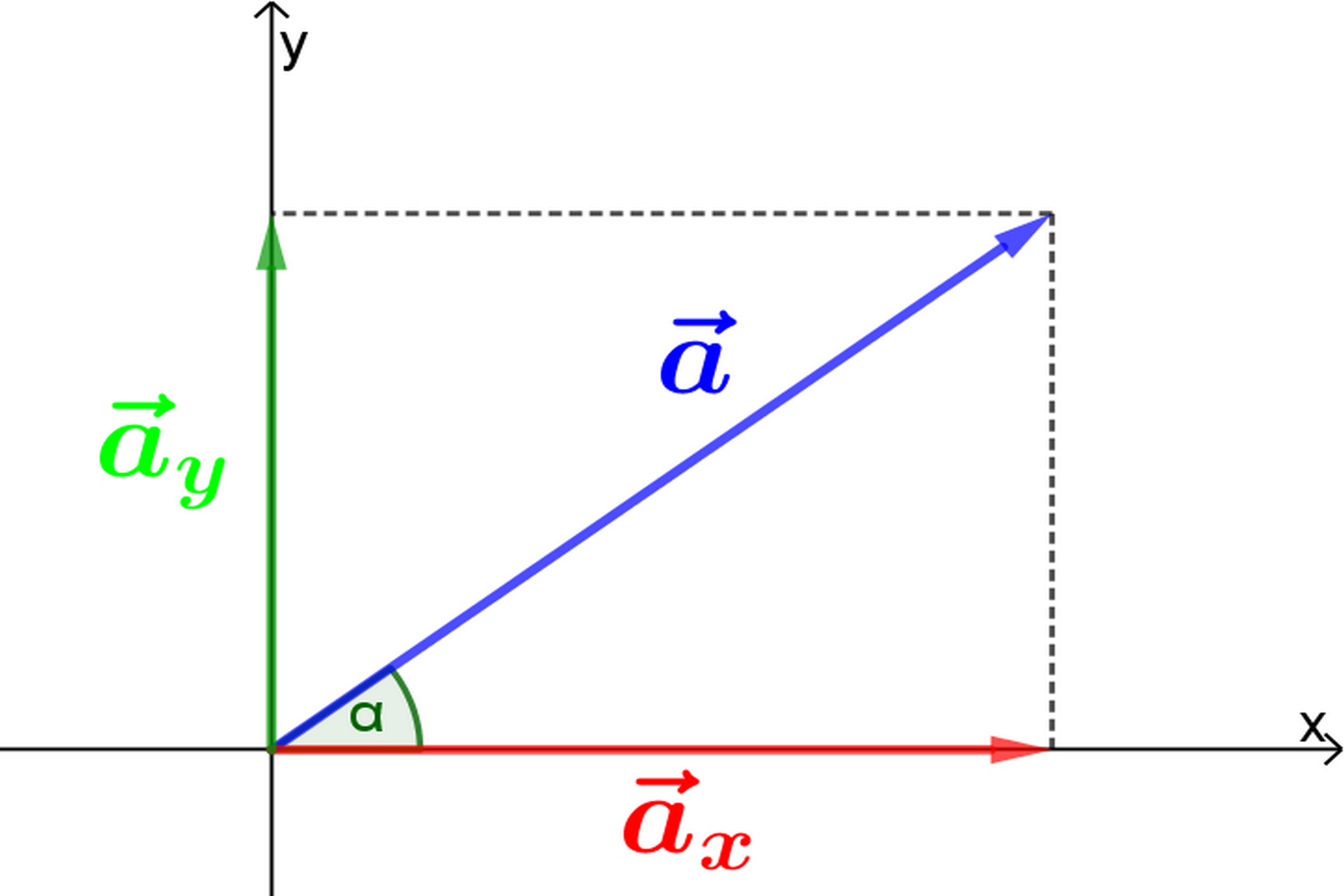
Se tracci in un piano cartesiano le due rette passanti per gli estremi di un vettore £$\overrightarrow{v}$£ e perpendicolari agli assi, ottieni le proiezioni del vettore sui due assi. Le lunghezze di tali proiezioni sono dette componenti del vettore lungo gli assi cartesiani.
Geometricamente: traccio il vettore £$\overrightarrow{a}$£, in modo che la sua coda coincida con l’origine del piano cartesiano; dalla punta del vettore £$\overrightarrow{a}$£ traccio le perpendicolari ai due assi cartesiani, individuando sui due assi le componenti, che partono dalla coda del vettore e arrivano fino al punti di intersezione.
Analiticamente: indicando con £$\alpha$£, ponendo per esempio £$\alpha=30°$£, l’angolo formato dal vettore £$\overrightarrow{a}$£, di modulo £$|a| = 5$£, con il semiasse positivo dell’asse x, otteniamo le due componenti applicando i teoremi della trigonometria:
£$a_x = |a| \cdot cos \alpha =5 \cdot \dfrac{\sqrt{3}}{2} $£ £$a_y = |a| \cdot sin \alpha = 5 \cdot \dfrac{1}{2}$£
Il vettore può essere a questo punto individuato anche mediante le sue componenti, indicandolo in due diversi modi:
£$\overrightarrow{a} (a_x;a_y) = a_x\hat{i} + a_y\hat{j} = 5\dfrac{\sqrt{3}}{2}\hat{i} + \dfrac{5}{2}\hat{j}$£
dove £$\hat{i}$£ e £$\hat{j}$£ sono, rispettivamente, i versori associati agli assi x e y del piano cartesiano.
Vettori e quadranti
Si può verificare (sia analiticamente che geometricamente) che:
se £$0° 0; a_y>0$£: in questo caso il vettore £$\overrightarrow{a}$£ con coda nell’origine del piano cartesiano ha la punta nel primo quadrante;
un esempio è il vettore £$3\hat{i} + 2 \hat{j}$£
se £$90° 0$£: in questo caso il vettore £$\overrightarrow{a}$£ con coda nell’origine del piano cartesiano ha la punta nel secondo quadrante;
un esempio è il vettore £$-3\hat{i} + 2 \hat{j}$£ o un vettore di modulo £$5$£ e £$\alpha = 120°$£
se [iol_placeholder type="formula" engine="katex" display="inline"]180°
come ad esempio il vettore di modulo £$3$£ ed £$\alpha = 225°$£, che si trova lungo la bisettrice del £$1°$£ e £$3°$£ quadrante
se [iol_placeholder type="formula" engine="katex" display="inline"]270° 0; a_y
un esempio di questo caso è il vettore £$5\hat{i} – 2 \hat{j}$£
Cosa sono i versori
Un vettore con direzione e verso qualsiasi, ma con modulo uguale a 1 viene chiamato vettore unitario, o versore, e viene indicato di solito con £$\hat v$£.
Un versore è utile per identificare una specifica direzione. Ogni vettore che si trovi lungo questa direzione può essere espresso con riferimento a questo versore: basta moltiplicare il versore per il modulo del vettore in questione, per ottenere il vettore stesso.
In un piano cartesiano possiamo definire i versori £$\hat i$£ e £$\hat j$£ associati rispettivamente alle direzioni dell’asse x e dell’asse y.
Quindi, ad esempio, otterremo il vettore £$\overrightarrow{a}$£ di modulo £$5$£ lungo l’asse x con £$5 \cdot \hat{i}$£, che ha come componenti £$a_x = 5$£ e £$a_y = 0$£
Analogamente, in uno spazio cartesiano a 3 dimensioni, possiamo definire i versori £$\hat i$£, £$\hat j$£ e £$\hat k$£ associati rispettivamente alle direzioni dell’asse £$x$£, dell’asse £$y$£ e dell’asse £$z$£.
Dato un qualunque vettore £$\overrightarrow{v}$£ con componenti £$v_x, v_y$£, si ha £$\overrightarrow{v} = v_x \hat i + v_y \hat j$£. Un ragionamento del tutto analogo può essere applicato a spazi cartesiani a più di 2 dimensioni.
Sono esempi di versori £$\dfrac{\sqrt{3}}{2} \hat{i} + \dfrac{1}{2} \hat{j}$£ , oppure £$\dfrac{\sqrt{2}}{2} \hat{i} – \dfrac{\sqrt{2}}{2} \hat{j}$£, che indica la direzione della bisettrice del £$2°$£ e £$4°$£ quadrante
Dalle componenti al vettore
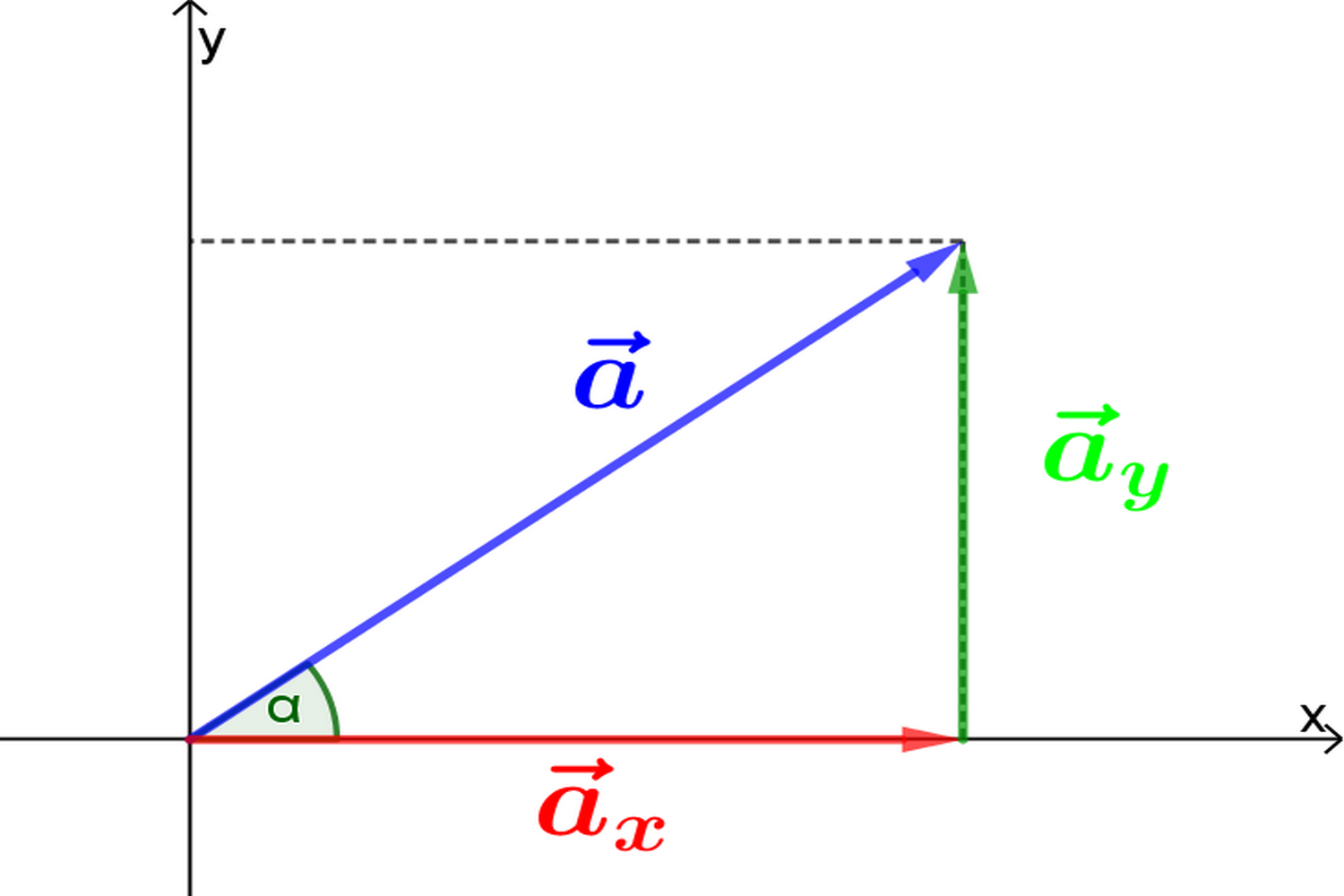
Per individuare univocamente un vettore possono essere date le sue componenti nel piano cartesiano, oppure il suo modulo e l’angolo che il vettore forma con il semiasse positivo dell’asse x. Abbiamo già visto che, dati modulo e angolo, possiamo ricavare la lunghezza delle componenti del vettore. Viceversa, possiamo determinare modulo e angolo a partire dalle componenti del vettore. Per determinare il modulo, è sufficiente applicare il teorema di Pitagora al triangolo rettangolo che ha come cateti le componenti del vettore e come ipotenusa il vettore stesso:
£$a = \sqrt{a_x^2 + a_y^2}$£
Per determinare l’angolo, è necessario usare le relazioni della trigonometria:
£$\alpha = arc tan\: \dfrac{a_y}{a_x}$£
Ad esempio se prendiamo il vettore £$\overrightarrow{a} = 3 \hat{i} + 4 \hat{j} $£, di componenti £$a_x = 3$£ ed £$a_y = 4$£ possiamo trovare il modulo:
£$a = \sqrt{3^2 + 4^2} = 5$£
e l’angolo:
£$\alpha = arctan\: \dfrac{4}{3} \simeq 53,13°$£
Questa funzione è individuata sulla calcolatrice scientifica come seconda funzione del tasto £$tan$£, ovvero £$tan^{-1}$£
Se hai ancora poca dimestichezza con le funzioni goniometriche, tieni presente la seguente osservazione:
Se £$a_x0$£ :
£$\alpha = arc tan\: \dfrac{a_y}{a_x} + 180°$£
Se £$a_x>0$£ e [iol_placeholder type="formula" engine="katex" display="inline"]a_y £$\alpha = arc tan\: \dfrac{a_y}{a_x} + 360°$£
Nel caso in cui il vettore sia nel primo quadrante, il risultato della calcolatrice ti fornirà l’angolo formato dal vettore con la direzione positiva dell’asse x in gradi, senza bisogno di fare altro.
