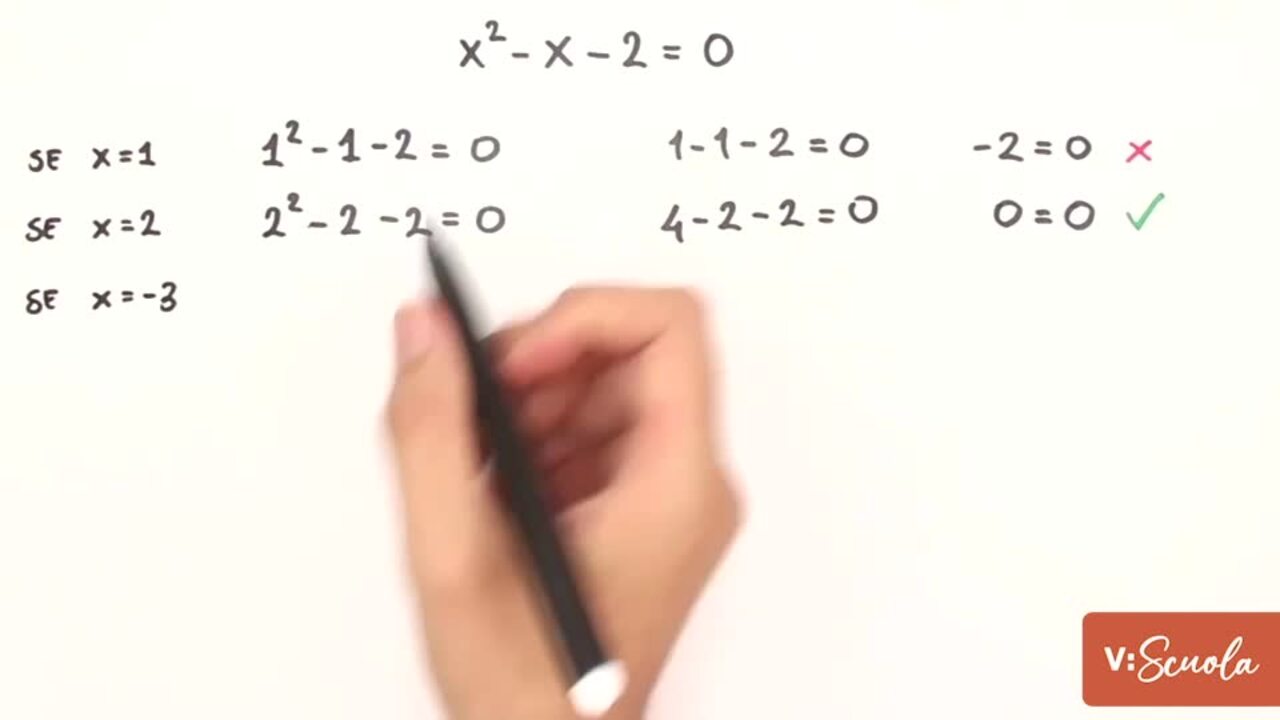Come si risolvono le equazioni di secondo grado
Equazioni di secondo grado: cosa sono e come si risolvono? A che cosa servono le radici in matematica? Se cerchi le risposte a queste domande leggi questa lezione sulle equazioni di secondo grado.
Le equazioni di secondo grado ad un’incognita sono anche chiamate equazioni di grado 2 o equazioni quadratiche: sono delle equazioni nelle quali ritroviamo un’incognita che ha un esponente di secondo grado.
Scoprirai in questa lezione che, se ridurrai l’equazione alla forma normale, potrai risolverla con un’unica e semplice formula. Vediamola insieme!
- Cosa sono le equazioni di secondo grado
- Definizione di equazione di secondo grado
- Come risolvere le equazioni di secondo grado
- Formula per risolvere le equazioni di secondo grado
Cosa sono le equazioni di secondo grado
Le equazioni di secondo grado o quadratiche sono equazioni algebriche del tipo £$ax^2+bx+c=0$£, dove £$a, b$£ e £$c$£ si chiamano coefficienti e £$c$£ in particolare si dice termine noto.
Un’equazione di secondo grado, ridotta in forma normale al tipo £$ax^2+bx+c=0$£, è detta anche equazione di secondo grado completa poichè l’incognita £$x$£ compare al grado £$2$£ e al grado £$1$£ prima del termine noto.
Il tuo scopo sarà quello di trovare i valori dell’incognita £$x$£ che rendano l’equazione di secondo grado un’identità.
Allora come risolvere le equazioni di secondo grado? I valori di £$x$£ che devi cercare sono detti soluzioni o radici dell’equazione.
Esiste una formula risolutiva che ti permette di risolvere qualunque equazione di secondo grado: £$x_{1,2}=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$£ dove la quantità sotto radice £$\Delta=b^2-4ac$£ è chiamata discriminante o delta. Le equazioni lineari ammettevano al massimo una sola soluzione mentre le equazioni di secondo grado possono averne fino a due: calcolando il delta saprai subito quante soluzioni ha la tua equazione di secondo grado: due soluzioni se £$\Delta>0$£, una soluzione se £$\Delta=0$£, zero soluzioni se £$\Delta<0$£.
Definizione di equazione di secondo grado
Che cos’è un’equazione di secondo grado e che cosa sono le radici
Cosa sono le equazioni di secondo grado? £$3x^2-7x+3=0$£ è un’equazione di secondo grado come £$-x^2=0$£ o £$2x^2+3=0$£. Le equazioni di secondo grado complete sono quindi della forma normale £$ax^2+bx+c=0$£
Ricordati che £$a$£ non può essere uguale a zero altrimenti l’equazione diventa £$bx+c=0$£ che è di primo grado! £$a$£, £$b$£ e £$c$£ si chiamano coefficienti e £$c$£ ha anche un altro nome: termine noto!
I valori che sostituiti all’incognita £$x$£ rendono vera l’uguaglianza sono detti soluzioni o radici dell’equazione di secondo grado. Per esempio £$x^2-x-2=0$£ ha per soluzioni £$x=-1$£ e £$x=2$£ infatti:
- £$(-1)^2-(-1)-2=0 \to 1+1-2=0 \to 0=0 $£ che è un’identità
- £$ 2^2-(2)-2=0 \to 4-2-2=0 \to 0=0 $£ che è un’identità
Scoprirai che le equazioni di secondo grado possono avere una, due o nessuna soluzione nell’insieme dei numeri reali!
Come risolvere le equazioni di secondo grado
Metodo geometrico del completamento del quadrato
Metodo algebrico del completamento del quadrato
C’è un metodo per risolvere le equazioni di secondo grado: il metodo del completamento del quadrato!
Questa tecnica consiste nel trasformare un’equazione di secondo grado come £$-3x^2+5x+2=0$£ in "£$(x+…..)^2=\text{numero}$£" cioè al primo membro vogliamo un quadrato di un binomio e a secondo membro un numero. I passaggi da seguire sono:
- Se il coefficiente di £$x^2$£ è negativo cambiamo i segni a tutti i membri dell’equazione, quindi £$-3x^2+5x+2=0$£ diventa £$3x^2-5x-2=0$£
- Porta a secondo membro il termine noto £$3x^2-5x=2$£
- Se il coefficiente di £$x^2$£ è diverso da £$1$£ dividi tutti i termini per il coefficiente di £$x^2$£ che hai, quindi £$3x^2-5x=2$£ diventa £$x^2-\frac{5}{3}x=\frac{2}{3}$£
- Ora devi trovare il numero da mettere al posto dei puntini £$x^2-\frac{5}{3}x+\ldots =\frac{2}{3}+\ldots $£ per fare in modo che a primo membro ci sia lo sviluppo del quadrato di un binomio: prendi il coefficiente di £$x$£, dividilo per £$2$£ ed elevalo al quadrato £$(\frac{5}{3}:2)^2=\frac{25}{36}$£. Quindi abbiamo £$x^2-\frac{5}{3}x+\frac{25}{36}=\frac{2}{3}+\frac{25}{36}$£ che diventa £$(x-\frac{5}{6})^2=\frac{49}{36}$£
- Fai la radice quadrata di entrambi i membri, ricordandoti di mettere il £$+$£ e £$–$£ al secondo membro! £$\sqrt{(x-\frac{5}{6})^2}=\pm \sqrt{\frac{49}{36}}$£ che diventa £$x-\frac{5}{6}=\pm \frac{7}{6}$£
- Ottieni quindi due equazioni lineari! £$x-\frac{5}{6}=\frac{7}{6}$£ che ha soluzione £$x=2$£ e £$x-\frac{5}{6}=-\frac{7}{6}$£ che ha soluzione £$x=-\frac{1}{3}$£
Con questo metodo puoi risolvere tutti i tipi di equazione di secondo grado tranne quelle del tipo £$ax^2+c=0$£, cioè quelle spurie.
Formula per risolvere le equazioni di secondo grado
Qual è la formula risolutiva?
Cos’è il delta?
Vogliamo trovare una formula da applicare sempre per risolvere una qualsiasi equazione di secondo grado. Per trovarla usiamo il metodo del completamento del quadrato all’equazione di secondo grado scritta in forma normale £$ax^2+bx+c=0$£. Facendo i calcoli abbiamo £$ x_{1,2}=\frac{-b \pm \sqrt{b^2-4ac}}{2a}$£ che è la formula risolutiva delle equazioni di secondo grado!
Ma quante soluzioni ha un’equazione di secondo grado? Dalla formula sembrerebbe sempre due, ma dipende dalla quantità sotto radice, cioè £$b^2-4ac$£. Questa quantità è chiamata delta £$\Delta$£ o discriminante dell’equazione di secondo grado. Se il delta è £$ > 0$£ avremo due soluzioni distinte (perché rimane il £$\pm$£), se è £$=0$£ avremo due soluzioni coincidenti £$x_{1}=x_{2}$£ e se è £$ < 0$£ non esistono soluzioni reali, perché non esiste la radice quadrata di un numero negativo!