Numeri complessi: forma trigonometrica ed esponenziale
Hai visto che i numeri complessi si possono esprimere nella forma algebrica £$a+ib$£. Questo però non è l’unico modo che hai per scrivere un numero complesso. Ce ne sono altri due:
- forma trigonometrica £$\rho(cos\ \theta +isen\, \theta)$£
- forma esponenziale £$\rho e^{i\theta}$£
In questo articolo scoprirai cosa sono il modulo e l’argomento di un numero complesso, e imparerai come si scrivono i numeri complessi in forma trigonometrica e in forma esponenziale.
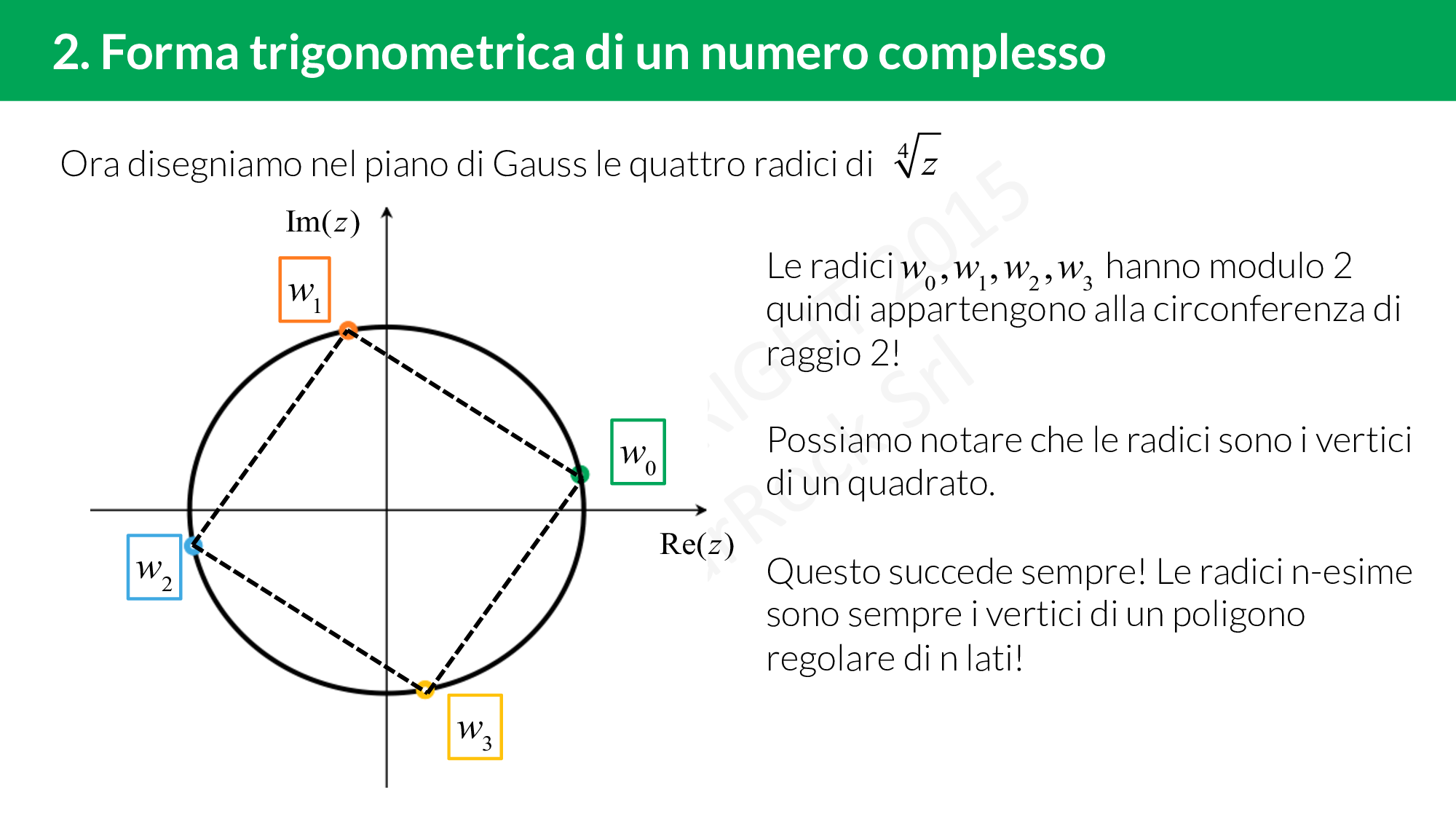
- Forma trigonometrica di un numero complesso
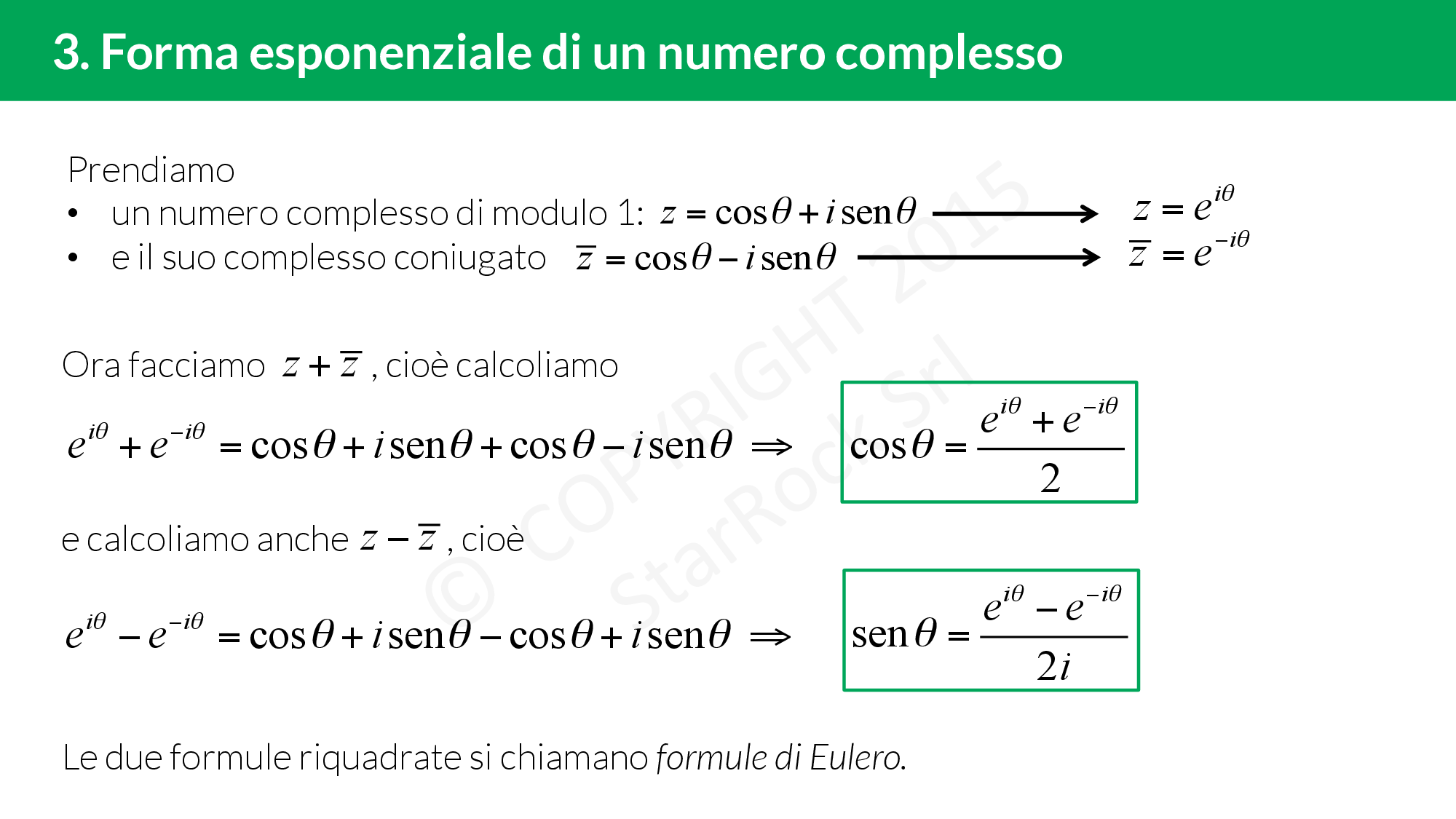
- Forma esponenziale di un numero complesso
- Esercizio su forma trigonometrica ed esponenziale esponenziale
Forma trigonometrica di un numero complesso
Modulo e argomento di un numero complesso
Forma trigonometrica
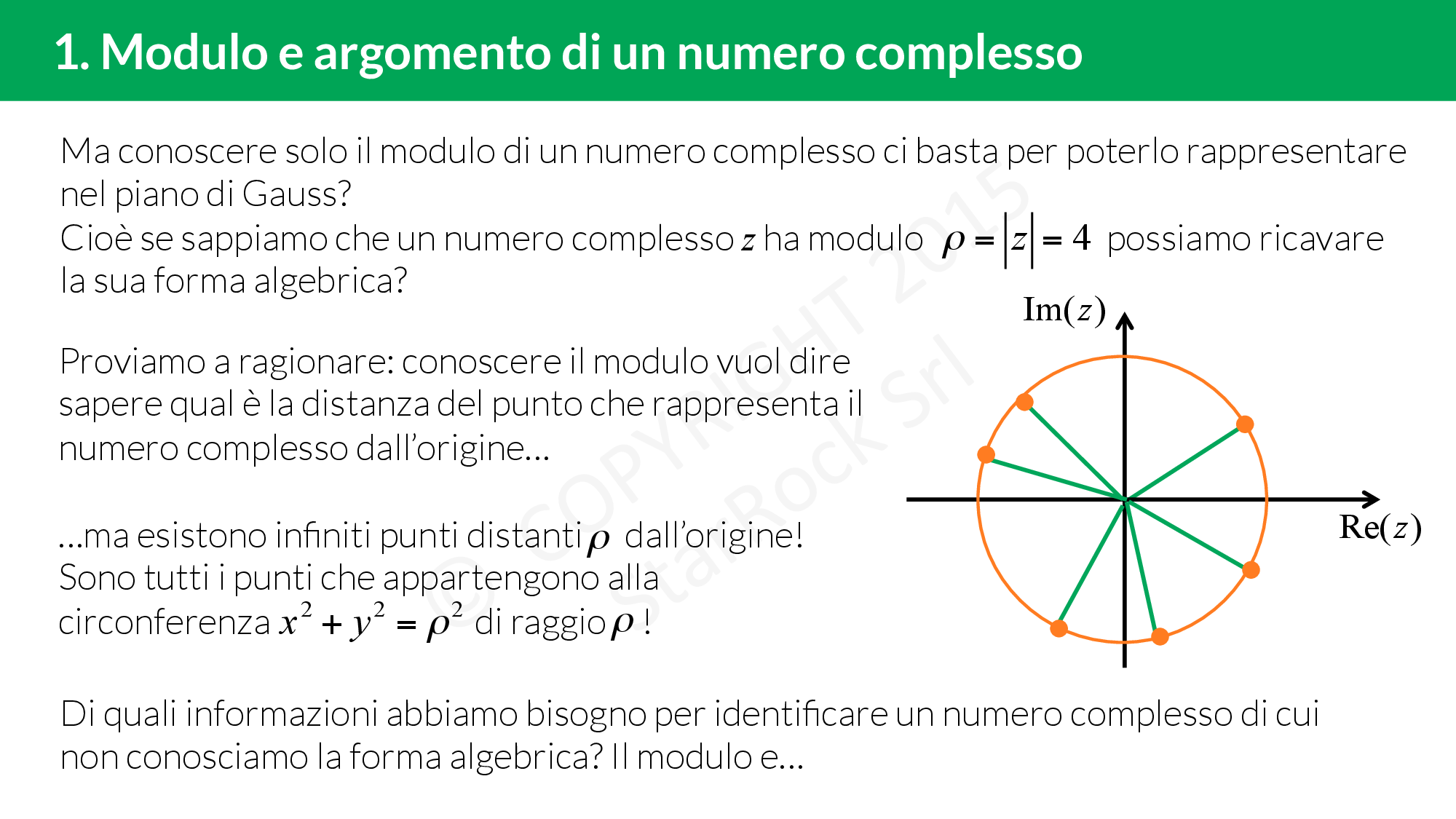
Ogni numero complesso può essere rappresentato graficamente nel piano di Gauss: immagina il tradizionale piano cartesiano, dove l’asse orizzontale rappresenta la parte reale dei numeri complessi e l’asse verticale la loro parte immaginaria. Ogni punto sul piano di Gauss corrisponde quindi a un numero complesso unico, con la sua coordinata orizzontale che indica la parte reale e quella verticale la parte immaginaria.
Ci viene subito in mente una cosa: possiamo identificare ciascun numero complesso anche in base alla distanza dall’origine e all’angolo che forma il segmento che unisce l’origine e il numero con l’asse delle ascisse.
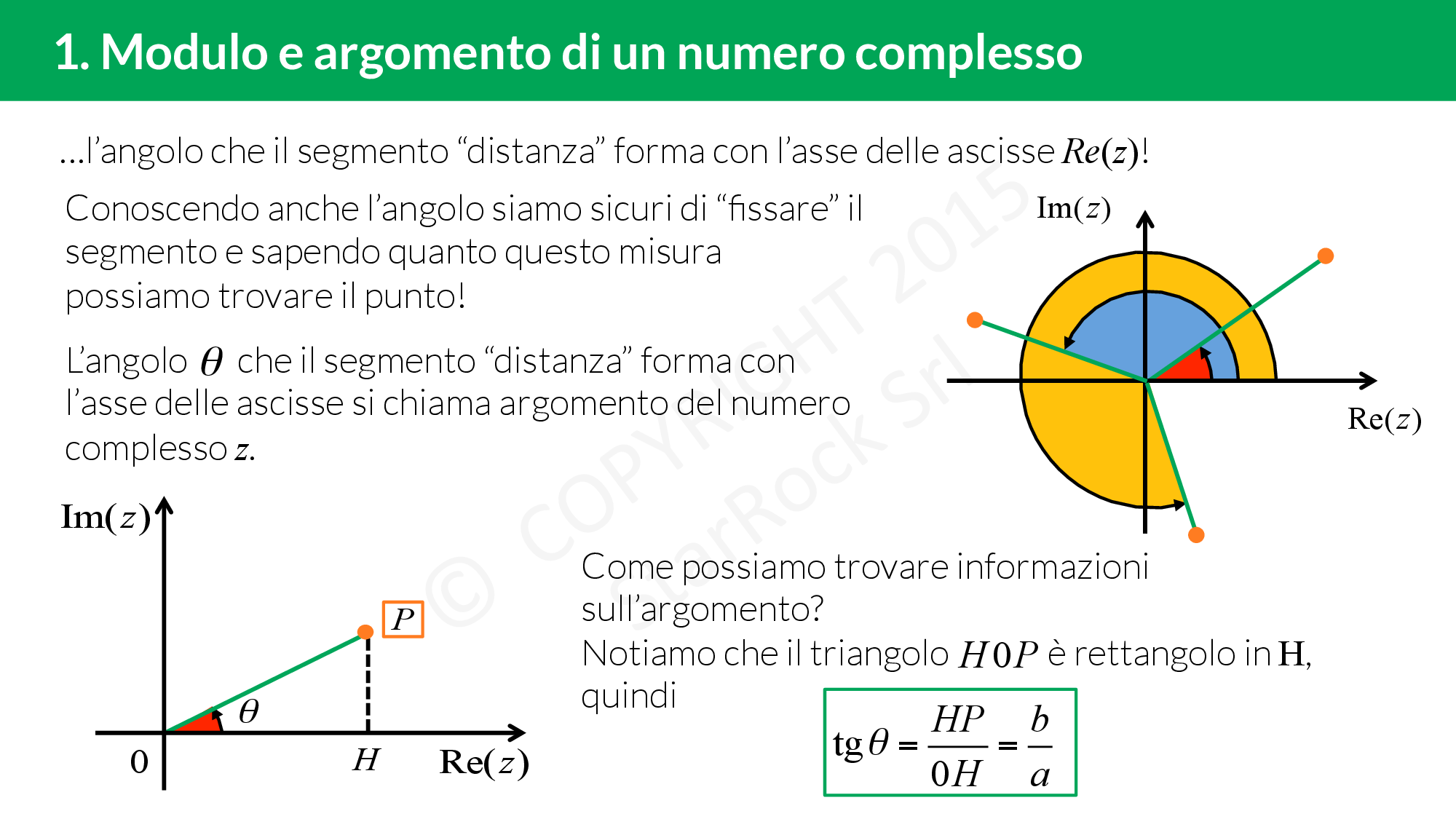
La distanza dall’origine viene chiama modulo del numero complesso, mentre l’angolo è l’argomento del numero complesso. Così abbiamo un nuovo modo per rappresentare i numeri complessi, che si chiama forma trigonometrica. Se £$z=a+ib$£ è il nostro numero complesso scritto in forma algebrica, avremo:
- £$ d(z,O)=\sqrt{a^2+b^2}=\rho $£ è il modulo
- se £$\theta $£ è l’argomento, abbiamo che £$tg\,\theta=\frac{b}{a}$£
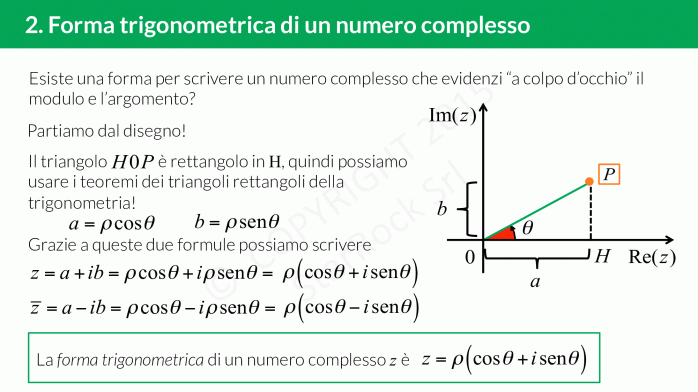
e il nostro numero complesso in forma trigonometrica sarà £$z=\rho(cos\,\theta+isen\,\theta)$£
Per trovare la forma trigonometrica dovrai trovare:
- il modulo £$\rho$£ del numero complesso £$a+ib$£ con la formula £$\rho=\sqrt{a^2+b^2} $£. Il modulo indica la distanza del punto £$(a;b)$£ dall’origine del piano di Gauss
- l’argomento £$\theta$£ (teta) del numero complesso £$a+ib$£ con la formula £$tg\theta=\frac{b}{a} $£. L’argomento indica, essendo un angolo, la distanza del segmento, congiungente £$(a;b)$£ con l’origine, dall’asse delle ascisse.
De Moivre: un po’ di storia

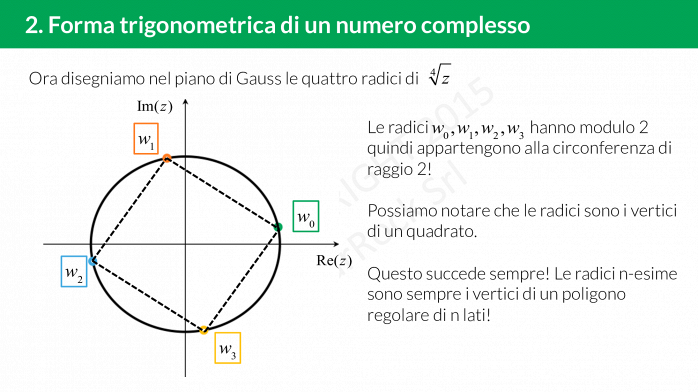
Il matematico francese Abraham De Moivre (1667-1754) introduce la forma trigonometrica dei numeri complessi cercando un metodo generale per estrarre la radice cubica da un numero complesso £$a+ib$£.
Sai come va a finire questa storia?
Forma esponenziale di un numero complesso
Ogni numero complesso può essere rappresentato anche in forma esponenziale.
Se £$z=\rho(cos\,\theta+isen\,\theta)$£ è il numero complesso, vale l’uguaglianza
$$\rho(cos\,\theta+isen\,\theta)=\rho e^{i \theta}$$
dove £$e$£ è il numero di Nepero.
La forma esponenziale è una diretta conseguenza di quella trigonometrica poiché si definisce £$e^{i\theta}= cos\, \theta+isen\, \theta$£.
Esercizio su forma trigonometrica ed esponenziale esponenziale

Ecco alcuni esercizi per allenarti con la forma trigonometrica e quella esponenziale dei numeri complessi. Sei capace di passare da una forma all’altra senza fare errori? Mettiti subito alla prova!