Angolo tra due rette: come si calcola
Calcolare l’angolo tra due rette è un concetto matematico fondamentale, particolarmente utile in geometria, design, architettura e in varie applicazioni ingegneristiche. Questo calcolo permette di determinare la misura dell’angolo formato dall’intersezione di due rette nel piano, fornendo una comprensione visiva e quantitativa della loro relazione spaziale.
Il processo per calcolare l’angolo tra due rette inizia con la determinazione delle pendenze di ciascuna retta. La pendenza di una retta, espressa matematicamente come il coefficiente angolare, è un indicatore della sua inclinazione rispetto all’asse orizzontale. In termini più semplici, la pendenza descrive quanto “ripida” è una retta: una pendenza maggiore indica una retta più inclinata.
Una volta note le pendenze delle due rette, si utilizza una formula specifica che mette in relazione queste pendenze con l’angolo cercato. Questa formula si basa sul concetto che l’angolo tra due rette è strettamente legato alla differenza delle loro inclinazioni. Matematicamente, l’angolo tra due rette può essere calcolato utilizzando la funzione arctangente delle loro pendenze, permettendo di ottenere la misura dell’angolo in gradi o radianti.
Scopriamolo insieme!
Tabella angolo aggiunto, angolo tra due rette, coefficiente angolare di rette perpendicolari
Tabella di riepilogo:
- metodo dell’angolo aggiunto,
- calcolo dell’angolo tra due rette e
- calcolo del coefficiente angolare di rette perpendicolari.
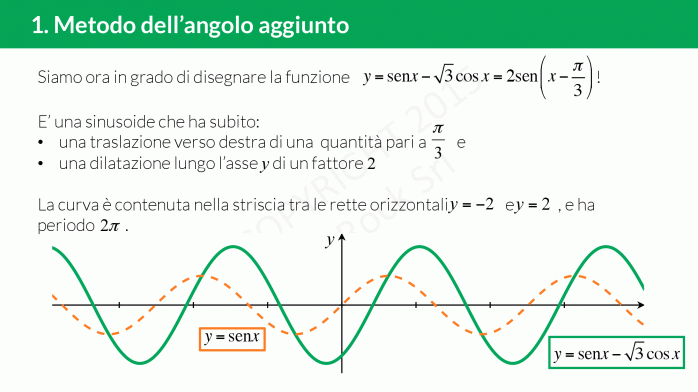
Metodo dell’angolo aggiunto
Metodo dell'angolo aggiunto e calcolo dell'angolo tra due rette: formule e dimostrazioni - Galleria
Il metodo dell’angolo aggiunto serve per trasformare, per mezzo delle formule di addizione e sottrazione, una funzione nella forma £$y=a \ sen \ x + b \ cos \ x $£ in una forma che sappiamo disegnare, cioè:
- £$y=Asen(x+\varphi)$£ oppure
- £$y=Acos(x+ \varphi)$£
L’angolo £$\varphi$£ (da cui prende il nome il metodo) si chiama angolo aggiunto.
Questo metodo è utile solo se conosciamo £$tg \varphi$£, altrimenti diventa comunque difficile disegnare la funzione!
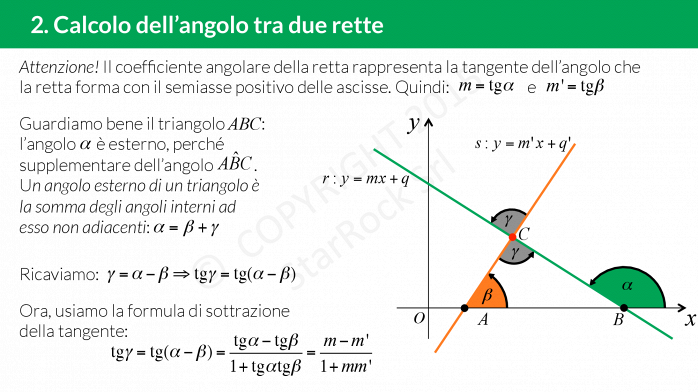
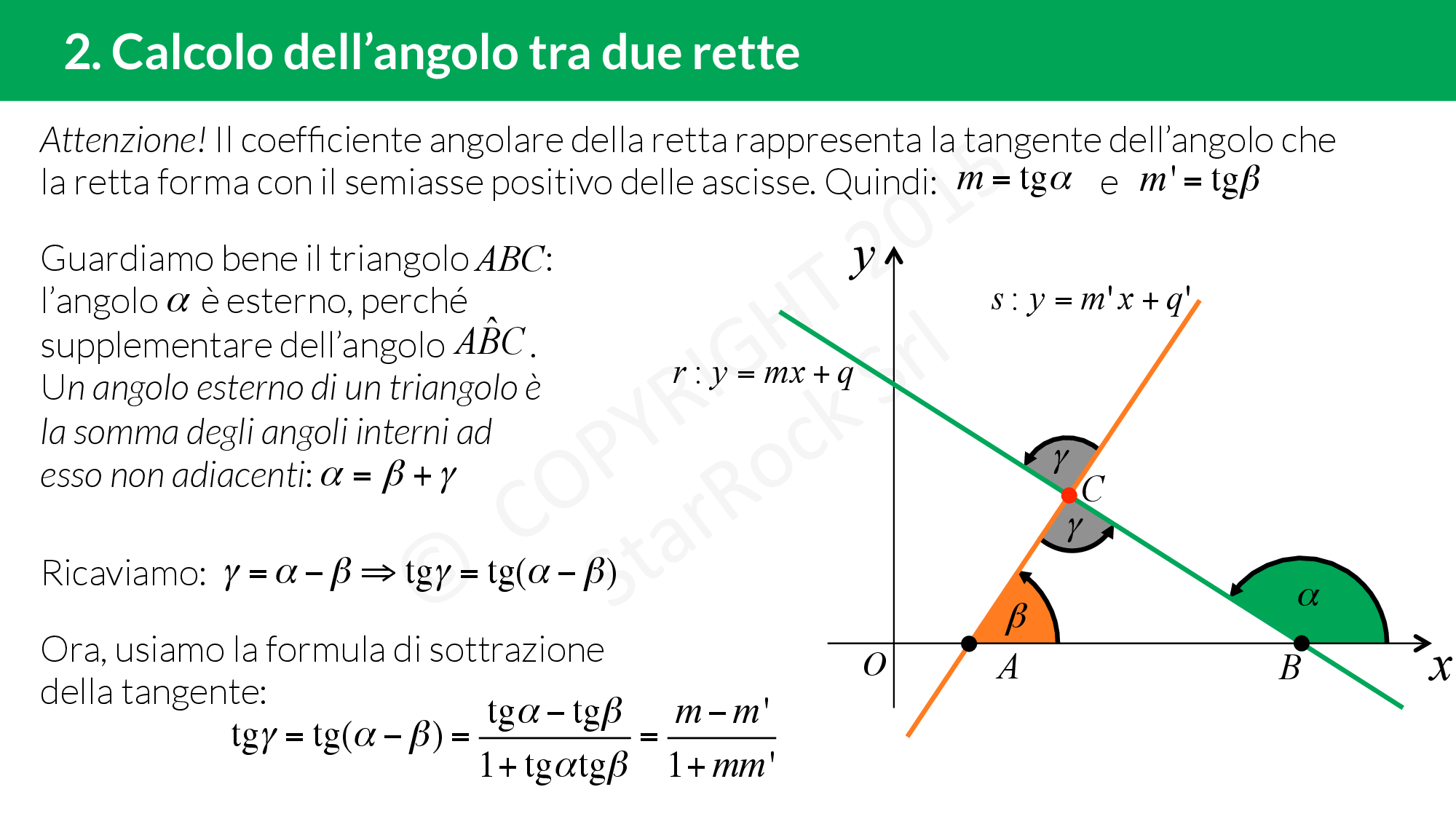
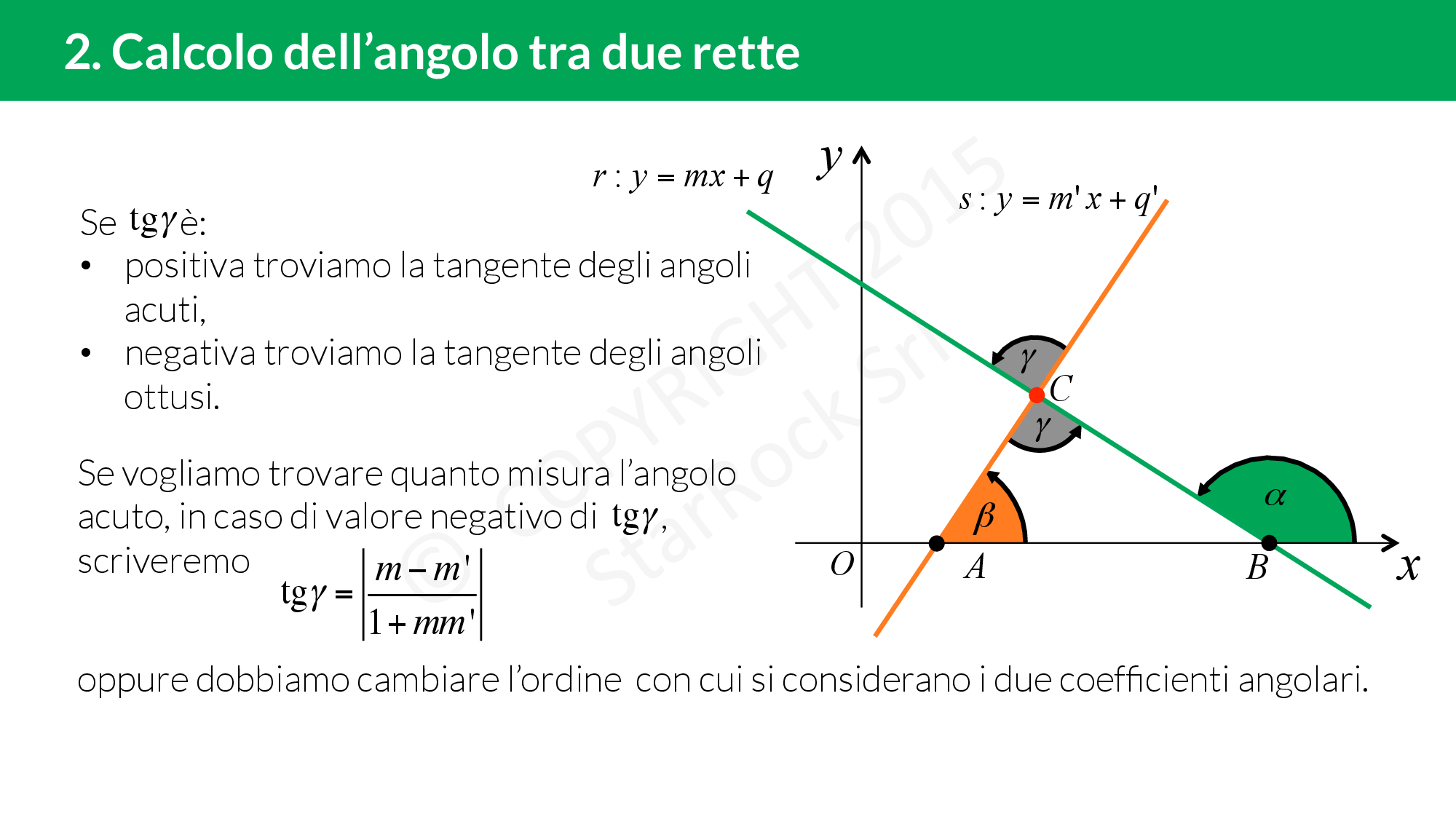
Calcolo dell’angolo tra due rette
Metodo dell'angolo aggiunto e calcolo dell'angolo tra due rette: formule e dimostrazioni - Galleria
Calcoliamo l’angolo tra due rette incidenti data l’equazione delle due rette.
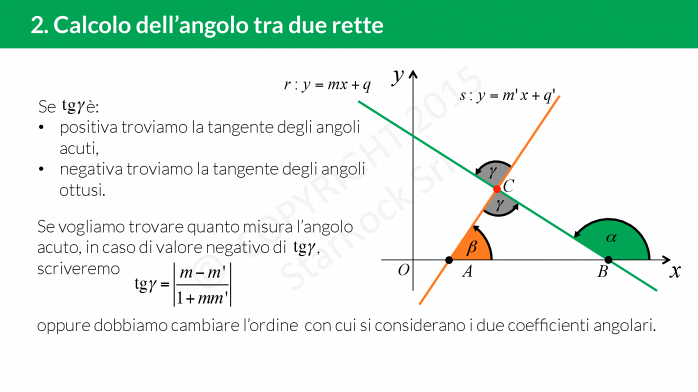
Possiamo determinare la tangente degli angoli che hanno come vertice comune il punto di incidenza delle due rette. Sia £$\gamma$£ uno degli angoli che vogliamo determinare, £$m$£ e £$m’$£ i coefficienti angolari delle rette, allora: £$tg \gamma=\left| \dfrac{m-m’}{1+mm’} \right|$£. Se:
- £$tg\gamma>0$£ allora £$\gamma$£ è un angolo acuto;
- [iol_placeholder type="formula" engine="katex" display="inline"]tg\gamma
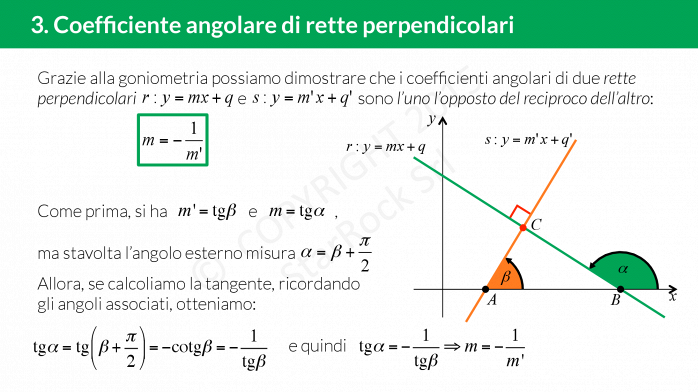
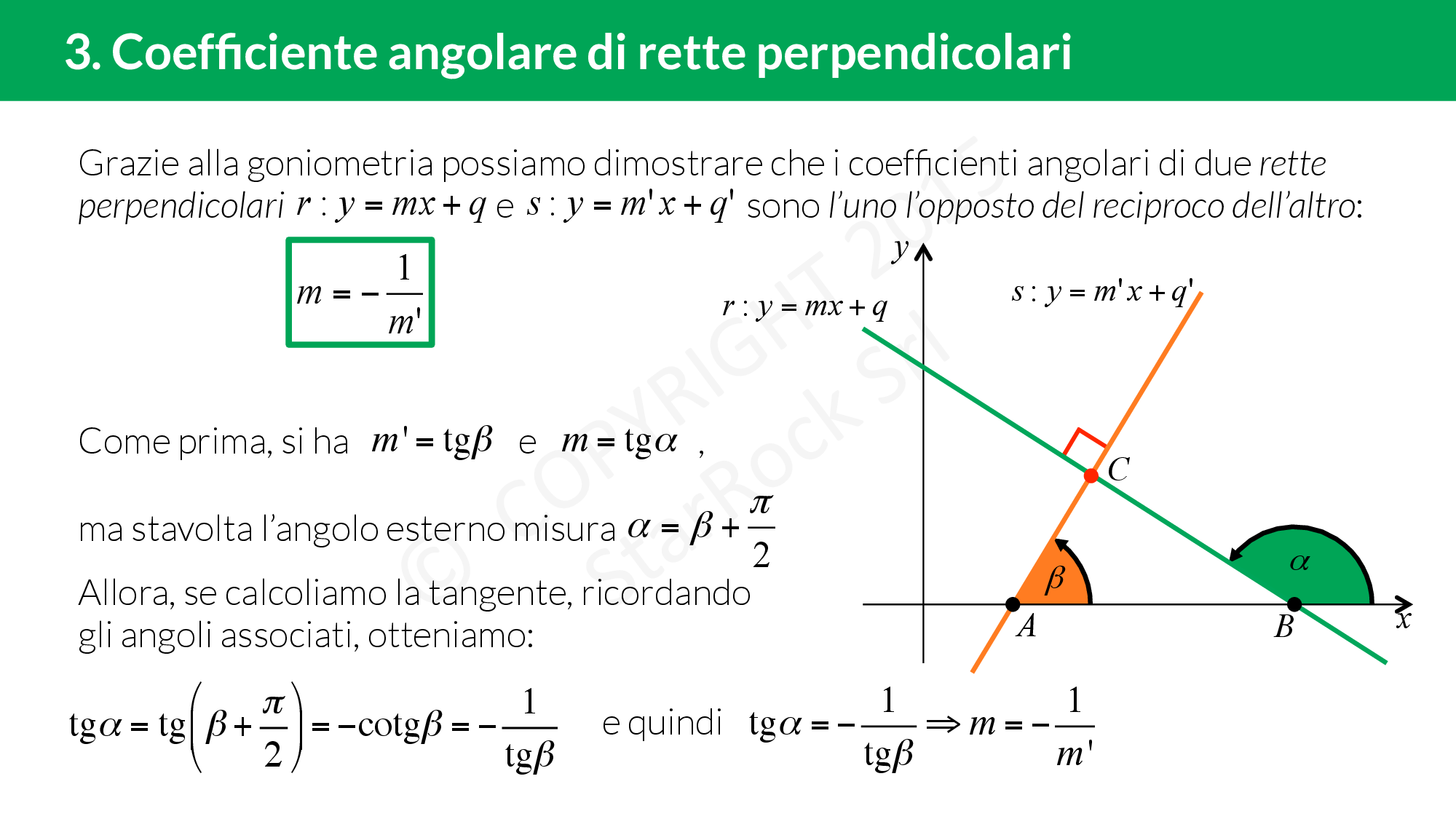
Coefficiente angolare di rette perpendicolari
Metodo dell'angolo aggiunto e calcolo dell'angolo tra due rette: formule e dimostrazioni - Galleria
Due rette perpendicolari hanno il coefficiente antireciproco, cioè date due rette con coefficiente angolare £$m$£ ed £$m’$£ queste sono perpendicolari se e solo se £$m=-\frac{1}{m’}$£.
Per la dimostrazione del legame fra i coefficienti angolari di rette perpendicolari possiamo usare il calcolo dell’angolo tra due rette.
Esercizi sul calcolo dell’angolo tra due rette
Metodo dell'angolo aggiunto e calcolo dell'angolo tra due rette: formule e dimostrazioni - Galleria
Ora che hai visto alcune tecniche per semplificare le espressioni goniometriche e il significato della tangente di un angolo, mettiti alla prova con gli esercizi!