Massimi e minimi: funzioni in due variabili
Massimi e minimi di una funzione: cosa sono
Spesso abbiamo parlato di massimi e minimi per le funzioni in una variabile reale.
Ora vediamo di generalizzare la definizione per funzioni in due variabili.
Definizione: data una funzione £$z=f(x,y)$£ definita in un insieme £$D$£, diciamo che il punto £$P_{0}(x_{0};y_{0})$£ è un punto di massimo relativo per £$f$£ se esiste un intorno del punto £$P_{0}$£ in £$D$£ tale che per tutti i punti di questo intorno vale la relazione $$f(x,y)\le f(x_{0},y_{0})$$
Allo stesso modo viene definito il punto di minimo, sostituendo £$\ge $£ a £$\le$£.
Anche per le funzioni in due variabili, vale il teorema di Weierstrass:
Se una funzione £$f$£ è continua in un insieme chiuso e limitato £$S$£, esiste in questo insieme almeno un punto in cui la funzione assume valore massimo assoluto e almeno un punto in cui assume il valore minimo assoluto.
Se vuoi ripassare il teorema per le funzioni in una variabile, vai alla lezione sui teoremi delle funzioni continue.
Massimi e minimi con le curve di livello nelle funzioni a due variabili
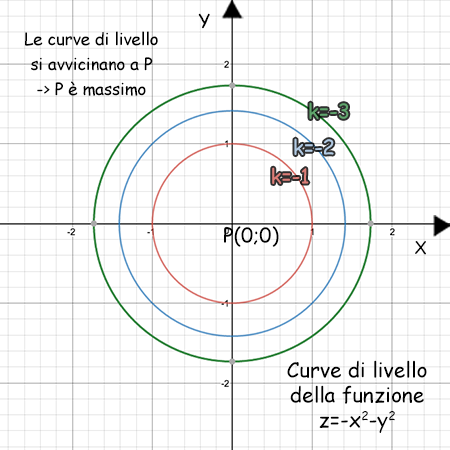
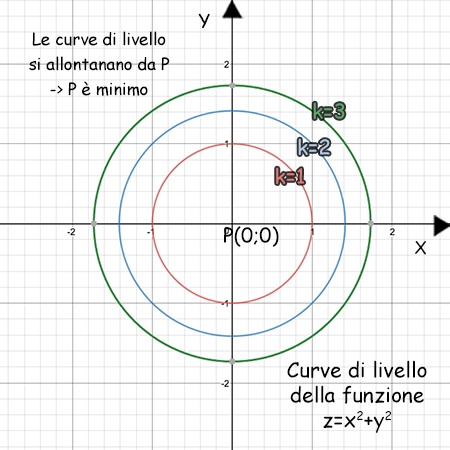
Il primo metodo per trovare i massimi e i minimi di una funzione in due variabili non c’entra molto con le derivate. Infatti usiamo le curve di livello, cioè le curve ottenute con una sezione della superficie con un piano orizzontale.
In pratica dobbiamo studiare le curve di livello al variare del valore di £$z=k$£:
- se le curve tendono ad allontanarsi dal punto £$P$£ al crescere di £$k$£ allora £$P$£ è un punto di minimo
- se le curve tendono ad avvicinarsi al punto £$P$£ al crescere di £$k$£ allora £$P$£ è un punto di massimo.
Massimi e minimi con le derivate per le funzioni a due variabili
Come per le funzioni in una variabile reale, anche per le funzioni in due variabili ricercare i massimi e i minimi è un processo che si può fare grazie alle derivate.
Infatti, una condizione necessaria affinché un punto £$P_{0}(x_{0},y_{0})$£ sia un estremante è che le derivate parziali valutate nel punto devono essere uguali a zero, cioè:
$$\begin{cases}f_{x}(x_{0},y_{0})=0 \\ f_{y}(x_{0},y_{0})=0 \end{cases}$$
ma questo non basta. Dobbiamo affidarci alle derivate parziali seconde. Abbiamo visto che le derivate parziali seconde sono quattro e con queste possiamo costruire la matrice hessiana
$$H_{f}=\left[ \begin{matrix} f_{xx} & f_{xy} \\ f_{yx} & f_{yy} \end{matrix} \right]$$
se le derivate parziali seconde sono continue nel dominio, allora possiamo calcolare l’hessiano di £$f$£ che viene indicato con £$H(x,y)$£. L’hessiano è il determinante della matrice hessiana
$$H(x,y)=\begin{vmatrix}f_{xx} & f_{xy} \\ f_{yx} & f_{yy} \end{vmatrix} = f_{xx} \cdot f_{yy} – f_{xy} \cdot f_{yx} $$
allora detto £$P_{0}(x_{0},y_{0})$£ è un punto stazionario (cioè annulla le derivate parziali prime):
1. se £$H(x_{0},y_{0})>0$£ e vale anche £$f_{xx} > 0 $£ allora £$P_{0}$£ è un punto di minimo;
2. se £$H(x_{0},y_{0}) > 0$£ e vale anche [iol_placeholder type="formula" engine="katex" display="inline"]f_{xx}
3. se [iol_placeholder type="formula" engine="katex" display="inline"]H(x_{0},y_{0})
4. se £$H(x_{0},y_{0}) = 0 $£ non si può dire nulla. Bisogna capire il tipo di punto usando un altro metodo, per esempio quello delle curve di livello.
Massimi e minimi vincolati in una funzione a due variabili: metodo elementare
In alcuni problemi (soprattutto quelli che si riferiscono a
situazioni reali) le variabili sono soggette a vincoli. Questo significa
che non possono assumere tutti i valori nel dominio, ma devono
rispettare determinate condizioni (vincoli). Ora vedremo uno dei due
metodi per determinare i massimi e i minimi vincolati.
METODO ELEMENTARE
Il primo metodo consiste nell’intersecare il vincolo con la
superficie. In questo modo, la funzione diventa dipendente da una
variabile. Ora basta studiare la funzione ottenuta studiando il segno
della derivata prima per determinare gli eventuali massimi e minimi.
ESEMPIO: studiamo i massimi e i minimi della funzione £$z=x^2+y^3$£ soggetti al vincolo £$y=x$£. Dato che i punti cercati devono stare sulla retta £$y=x$£ sostituamo il vincolo nella funzione: £$z=x^2+x^3$£. Ora la funzione dipende solo dalla variabile £$x$£ quindi cerchiamo gli estremanti con il metodo classico, cioè con lo studio del segno della derivata: £$z’=2x+3x^2=x(2+3x)\ge 0 $£. Studiando il segno, vediamo che la derivata è positiva per £$x 0$£. La funzione avrà quindi massimo per £$x=-\frac{2}{3}$£ e minimo per £$x=0$£. Per trovare le coordinate dei punti basta sostituire i valori nella funzione.
Metodo dei moltiplicatori di Lagrange per le funzioni a due variabili
Il secondo metodo viene chiamato metodo dei moltiplicatori di Lagrange. Questo metodo segue una serie di passaggi ben precisa. Intanto, sia £$f(x,y)$£ la funzione di cui bisogna determinare i massimi e i minimi e £$g(x,y)=0$£ l’equazione del vincolo. La funzione £$f$£ deve avere le derivate parziali seconde continue e le derivate di £$g$£ rispetto a £$x$£ e rispetto a £$y$£ non devono annullarsi contemporaneamente nel dominio della funzione £$f$£. Allora possiamo costruire una nuova funzione £$L$£, detta lagrangiana, che è una combinazione lineare tra le due:
$$L(x,y,\lambda)=f(x,y)+\lambda g(x,y) \quad \text{con } \lambda \in \mathbb{R}$$
La variabile £$\lambda$£ si chiama moltiplicatore di Lagrange. Allora, i punti di massimo e minimo liberi di £$L$£ sono punti di massimo e minimo vincolati per £$f$£.
A questo punto, dobbiamo procedere trovando i punti £$(x;y;\lambda)$£ che annullano contemporaneamente le derivate parziali di £$L$£. Così troviamo i punti stazionari (candidati a essere estremanti). Ma come fare a trovare una condizione sufficiente a stabilire la natura di questi punti? Usiamo la matrice hessiana orlata: $$H_{L}=\left[ \begin{matrix}0 & g_{x} & g_{y} \\ g_{x} & L_{xx} & L_{xy} \\ g_{y} & L_{yx} & L_{yy} \end{matrix}\right]$$
E ora calcoliamo il determinante di questa matrice:
£$ H(x,y,\lambda)=\begin{vmatrix}0 & g_{x} & g_{y} \\ g_{x} & L_{xx} & L_{xy} \\ g_{y} & L_{yx} & L_{yy} \end{vmatrix}= $£ £$ g_{x}g_{y}L_{xy}+g_{y}g_{x}L_{yx}-g_{y}^2 L_{xx}-L_{yy}g_{x}^2 $£
Ora, se £$P_{0}(x_{0};y_{0};\lambda_{0})$£ è un punto stazionario per £$L$£ dobbiamo controllare il segno dell’hessiano valutato in £$P_{0}$£:
1. se £$H(x_{0},y_{0},\lambda_{0})> 0$£ allora £$P_{0}$£ è un massimo libero per £$L$£ e un massimo vincolato per £$f$£;
2. se [iol_placeholder type="formula" engine="katex" display="inline"]H(x_{0},y_{0},\lambda_{0})
3. se £$H(x_{0},y_{0},\lambda_{0}) = 0$£ allora non si può dire nulla su £$P_{0}$£ e bisogna studiare in altro modo come si comporta la funzione £$L$£ in un intorno del punto.
