Funzioni tangente e cotangente: definizione e grafici

Agostino Sapienza

INSEGNANTE DI MATEMATICA

Sono nato a Reggio Calabria il 07/10/85. Mi sono diplomato nel 2005 all'Istituto Magistrale Statale Tommaso Gulli. Ho conseguito la laurea triennale in Relazioni Internazionali a Messina e in Economia Internazionale a Padova. Dopo un pò di anni negli studi commercialisti sono stato chiamato per una supplenza covid nella classe di insegnamento A47. Ho poi conseguito l'abilitazione a Trieste nel sostegno e sono entrato di ruolo nel 2023

L’analisi delle funzioni trigonometriche come la tangente e la cotangente di un angolo è fondamentale in matematica e fisica.

La tangente di un angolo in un triangolo rettangolo è definita come il rapporto tra il lato opposto all’angolo e il lato adiacente, mentre la cotangente è il reciproco della tangente. In altre parole, la cotangente è il rapporto tra il lato adiacente e il lato opposto.

Vediamo insieme la tangente e la cotangente di un angolo rappresentate come funzioni: dominio, codominio, simmetrie, periodo e il loro grafico: scopriamo come studiare queste funzioni. Come è il grafico della tangente e della cotangente? In quali punti non sono definite le funzioni tangente e cotangente?

In questa lezione imparerai:

Funzione tangente e cotangente: dominio e codominio delle funzioni tangente e cotangente
Proprietà della tangente e della cotangente: periodicità, simmetria, segno e monotonia delle funzioni tangente e cotangente
Grafici delle funzioni tangente e cotangente: grafico delle due funzioni e sue caratteristiche.

Grafici della funzione tangente e cotangente
Le funzioni tangente e cotangente
Proprietà della tangente e della cotangente
Grafici delle funzioni tangente e cotangente
Ripassa per l'interrogazione sulle funzioni
Sfida su tangente e cotangente

Grafici della funzione tangente e cotangente

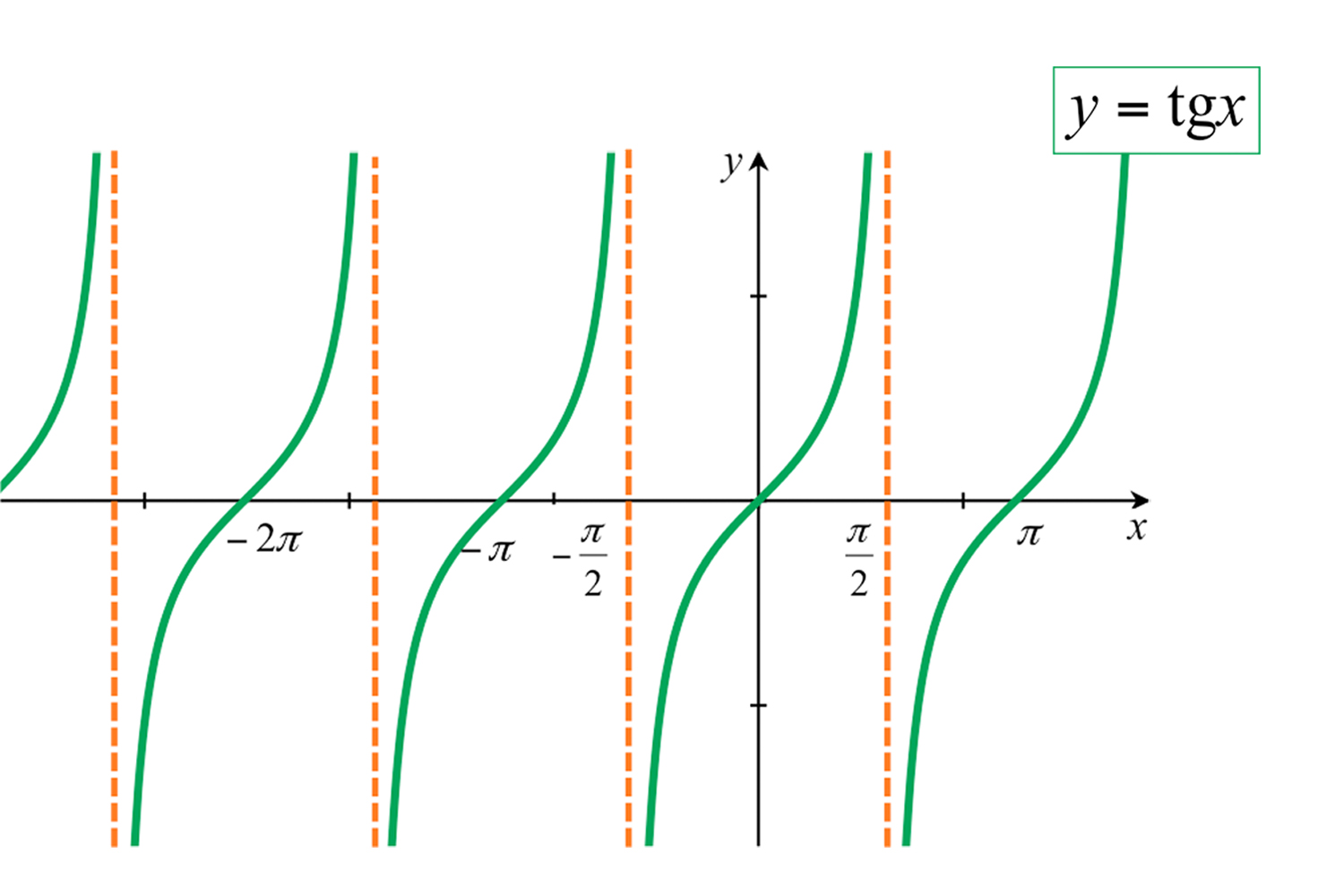
Tangente

Cotangente

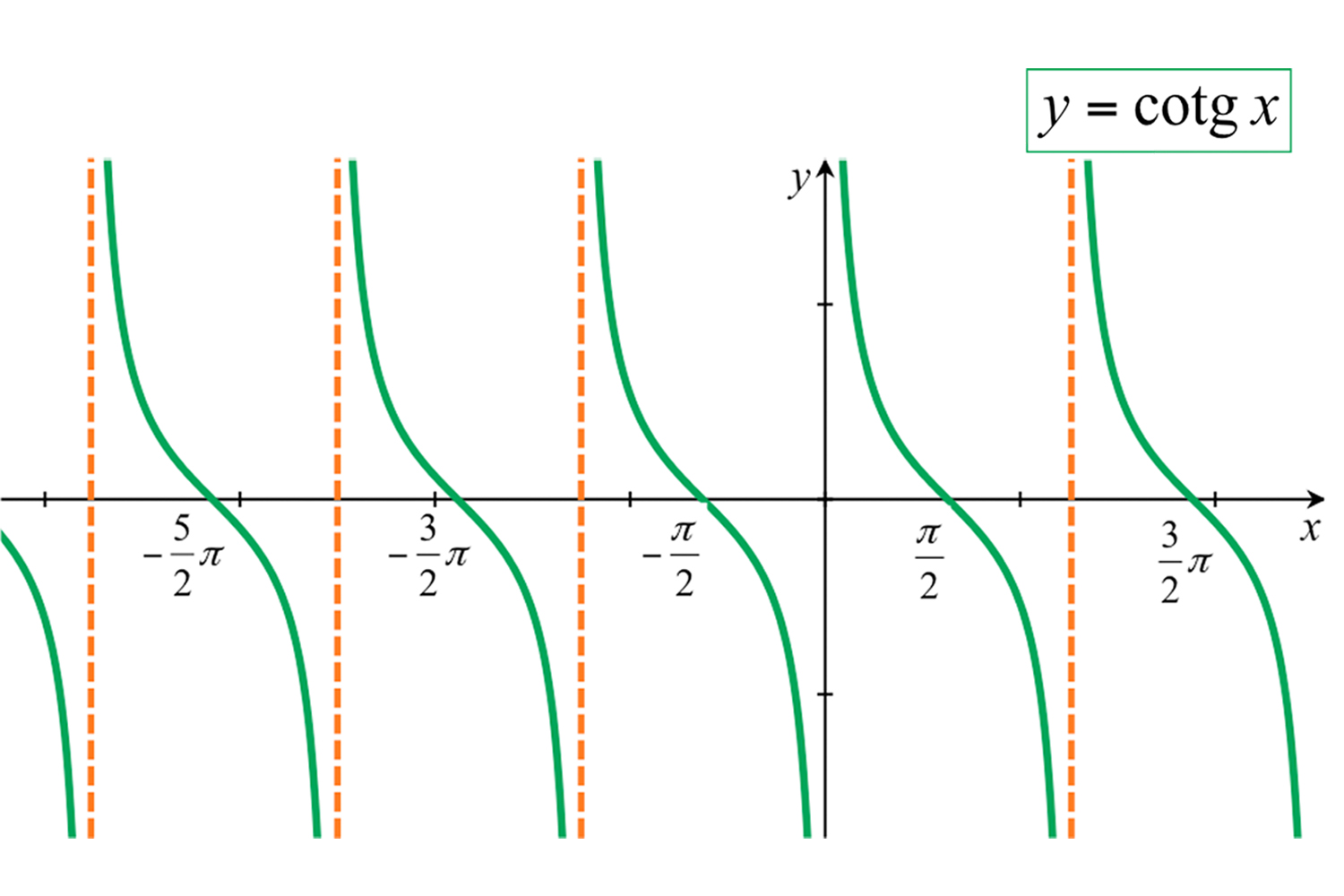
Grafici della funzione tangente e della funzione cotangente.

Le funzioni tangente e cotangente

Anche la tangente e la cotangente, come seno e coseno, possono essere viste univocamente in funzione di un angolo £$\alpha$£.

La tangente ha dominio l’insieme dei reali meno £$x=\frac{\pi}{2}+k\pi$£ con £$k $£ intero: £$\mathbb{R} \setminus \left\{\frac{\pi}{2}+k\pi, \ con \ k \ \in \mathbb{Z} \right\}$£.

La cotangente ha dominio l’insieme dei reali meno £$x=k\pi$£ con £$k $£ intero: £$\mathbb{R} \setminus \left\{k\pi, \ con \ k \ \in \mathbb{Z} \right\}$£.

Il codominio della tangente e della cotangente è invece tutto l’insieme £$\mathbb{R}$£ dei reali, perché possono assumere qualsiasi valore nei reali. Sono quindi funzioni suriettive.

Proprietà della tangente e della cotangente

Studiamo alcune proprietà delle funzioni tangente e cotangente che ci permettono di studiare più facilmente le due funzioni.

Periodicità. La tangente e la cotangente sono periodiche di 180°, cioè di £$\pi$£, quindi possiamo studiarle solo nell’intervallo £$(0, \pi)$£ e riportarle poi uguali negli altri intervalli:
- £$tg(x +k\pi) = tg \ x $£, £$x \ne \frac{\pi}{2}+k\pi$£ con £$k$£ intero;
- £$cotg(x +k\pi) = cotg \ x$£, £$x \ne k\pi$£ con £$k$£ intero.
Simmetria. La tangente e la cotangente sono simmetriche rispetto all’origine, possiamo quindi studiarle in un intervallo e poi fare la simmetria rispetto all’origine. Inoltre sfruttando la seconda relazione fondamentale della trigonometria e le proprietà di simmetria di seno e coseno puoi concludere che:
- la tangente è una funzione dispari: £$tg(-x)=-tg \ x $£;
- la cotangente è una funzione dispari: £$cotg(-x)=-cotg \ x $£.

Segno e monotonia. Studiamo il segno e la monotonia delle funzioni tangente e cotangente nell’intervallo £$(0,2\pi)$£.
- La funzione tangente £$ y=tg \ x \ $£ è:
  - positiva in £$\left(0,\frac{\pi}{2} \right) \cup \left( \pi, \frac{3}{2}\pi \right)$£;
  - negativa in £$\left(\frac{\pi}{2}, \pi \right) \cup \left( \frac{3}{2}\pi,2\pi \right)$£;
  - nulla in £$x=0, \pi$£;
  - sempre monotona crescente, cioè è crescente in tutto l’intervallo £$\left[0,2\pi \right] \setminus \left\{\frac{\pi}{2}, \frac{3}{2}\pi \right\}$£.
- La funzione cotangente £$ y=cotg \ x $£ è:
  - positiva in £$\left(0,\frac{\pi}{2} \right) \cup \left( \pi, \frac{3}{2}\pi \right)$£;
  - negativa in £$\left(\frac{\pi}{2}, \pi \right) \cup \left( \frac{3}{2}\pi,2\pi \right)$£;
  - nulla in £$x=\frac{\pi}{2}, \frac{3}{2}\pi $£;
  - sempre monotona decrescente, cioè decrescente in tutto l’intervallo £$\left[0,2\pi \right] \setminus \left\{0, \pi \right\}$£.

Grafici delle funzioni tangente e cotangente

Vediamo ora i due grafici della tangente e della cotangente. Notiamo che:

per la tangente le rette £$x=\frac{\pi}{2}+k\pi$£ con £$k$£ intero, sono asintoti;
per la cotangente le rette £$x=k\pi$£ con £$k$£ intero, sono asintoti.

I grafici delle funzioni tangente e cotangente si chiamano rispettivamente tangentoide e cotangentoide.