Prerequisiti per imparare traslazioni, simmetrie e omotetie di funzioni goniometriche
I prerequisiti per imparare traslazioni, simmetrie e omotetie di funzioni goniometriche sono:
Caricamento in corso...
Traslazioni, simmetrie e omotetie di funzioni goniometriche
Scopri come disegnare i grafici delle funzioni goniometriche dopo aver applicato delle trasformazioni come traslazioni, simmetrie e omotetie. Nella lezione successiva puoi scoprire i grafici con valore assoluto e come calcolare il periodo di una funzione goniometrica!
Appunti
Le trasformazioni geometriche di funzioni goniometriche sono le traslazioni, le omotetie o le simmetrie applicate a seno, coseno, tangente e cotangente. Come cambia il grafico di una funzione goniometrica a cui è stata applicata una trasformazione geometrica? Vediamo come cambiano le curve!
In questa lezione imparerai:
- traslazioni lungo gli assi: come cambia il grafico delle funzioni goniometriche applicando una traslazione;
- simmetrie, dilatazioni, compressioni: come cambia il grafico delle funzioni goniometriche applicando un'omotetia.
Contenuti di questa lezione su: Traslazioni, simmetrie e omotetie di funzioni goniometriche
Traslazioni lungo gli assi
Per traslare tutte le funzioni goniometriche orizzontalmente, e quindi lungo la direzione dell'asse £$x$£, dobbiamo aggiungere una costante all'argomento della funzione:
£$y=sen \ (x+a)$£ con £$a \in \mathbb{R}$£ è una traslazione orizzontale perché abbiamo aggiunto la costante £$a$£ all'argomento del seno!
- Se £$a>0$£ la traslazione è verso sinistra di un intervallo lungo £$|a|$£;
- se £$a<0$£ la traslazione è verso destra di un intervallo lungo £$|a|$£.
Per traslare tutte le funzioni goniometriche verticalmente, e quindi lungo la direzione dell'asse £$y$£ dobbiamo aggiungere una costante al valore della funzione:
£$y=cos \ x + b=b+cos \ x$£ è una traslazione verticale perché abbiamo aggiunto una costante al valore della funzione e non solo al suo argomento!
- Se £$b>0$£ la traslazione è verso l'alto di un intervallo lungo £$|b|$£;
- se £$b<0$£ la traslazione è verso il basso di un intervallo lungo £$|b|$£.
Trovi gli esercizi su questi argomenti nella lezione successiva.
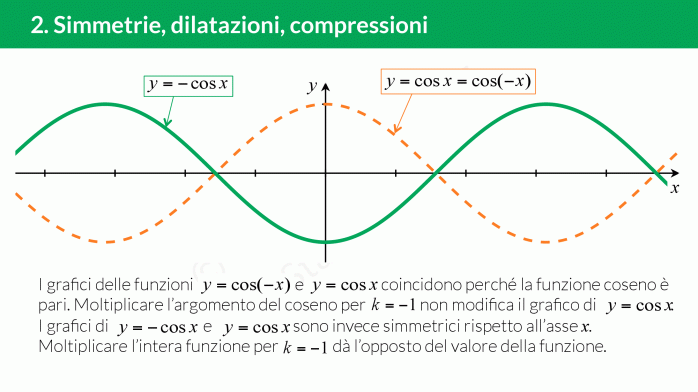
Simmetrie, dilatazioni, compressioni dei grafici
Moltiplicando l'argomento di una funzione goniometrica, oppure l'intera funzione goniometrica per una costante £$k$£, il grafico della funzione si dilata o si comprime. Stiamo applicando un'omotetia!
Cosa accade moltiplicando l'argomento, per esempio, di £$y=sen \ x$£ per £$k \in \mathbb{R}$£?
La nuova funzione è £$y=sen \ kx$£, il grafico subisce una trasformazione "orizzontale", ossia abbiamo:
- una compressione lungo l'asse £$ x $£ se £$k > 1$£;
- una dilatazione lungo l'asse £$ x $£ se £$0<k<1$£.
Il codominio rimane lo stesso della funzione goniometrica di partenza, ma le "onde" sono rispettivamente più o meno frequenti.
Cosa accade invece se moltiplichiamo tutta la funzione, per esempio £$y=sen \ x$£, per £$k \in \mathbb{R}$£?
La nuova funzione è £$y=k \ sen \, x$£, il grafico viene trasformato in "verticale", ossia abbiamo:
- una compressione lungo l'asse £$ y $£ se £$0<k<1$£;
- una dilatazione lungo l'asse £$ y $£ se £$k > 1$£.
La funzione interseca l'asse £$x$£ sempre negli stessi punti ma cambia il codominio, per esempio il seno o il coseno saranno contenuti nella fascia compresa fra le rette £$y=-k$£ e £$y=k$£ e non più £$y=-1$£ e £$y=1$£.
Se £$k<0$£ dobbiamo ragionare prima sulle simmetrie delle funzioni goniometriche e poi comporle con le omotetie.
Trovi gli esercizi su questi argomenti nella lezione successiva.
